Магический жезл
Магический жезл
Конечно, большинство переводчиков переведут Magic Wand (Магический жезл) как более привычное для нас «волшебная палочка». Однако инструмент с такими возможностями заслуживает и соответствующего названия. На первый взгляд его способность всего-навсего выделять контуры не производит большого впечатления, но в умелых руках этот инструмент становится по-настоящему магическим.
Инструмент Magic Wand (Магический жезл) можно активизировать одним из способов:
• командой главного меню ArchiCAD Design ? Outline Polygon with Magic Wand (Проектирование ? Выделение контура магическим жезлом);
• щелчком на кнопке Magic Wand (Магический жезл)
палитры Control Box (Палитра управления);
• нажатием и удержанием клавиши Пробел при нахождении в режиме построения объекта.
Совет
Настоятельно рекомендуется использовать второй способ из-за его простоты и удобства.
После активизации инструмента указатель мыши может принимать следующие формы:
•
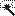
– при установке указателя мыши на характеристическую точку объекта;
•
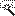
– при установке указателя мыши на ребро объекта;
•
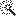
– при установке указателя мыши на грань объекта, заштрихованную область или пустое место.
Магический жезл работает в 2D– и 3D-окнах и распознает следующие типы элементов: стена, балка, перекрытие, крыша, штриховка, сетка, линия, дуга, полилиния и сплайн.
Принцип работы этого инструмента прост. Если щелчок кнопкой мыши производится на характеристической точке или ребре объекта, то магический жезл отслеживает форму контура, которому принадлежит указанная точка или ребро, и строит поверх исходного контура его копию. Если щелчок кнопкой мыши выполняется внутри замкнутого пространства, ограниченного какими-либо объектами, то магический жезл ищет контур, который ограничивает это пространство, вне зависимости от того, каким объектам принадлежат границы, и строит копию этого контура.
Внимание!
Отличительная особенность магического жезла, на которую не обращают внимания многие пользователи, – этот инструмент ищет контур, образованный любыми объектами, но строит в соответствии с найденным контуром объект того типа, который активизирован в данный момент.
Результаты работы этого инструмента порой настолько поразительны, что начинаешь понимать, почему разработчики ArchiCAD дали ему такое название.
Предположим, нужно построить колонну с каннелюрами – вертикальными ложбинками, идущими вдоль образующей (греческую колонну). Сечение такой фигуры имеет вид зубчатого колеса. Подобного сечения нет в стандартных библиотеках ArchiCAD, а в обширном списке объектов, с которыми работает магический жезл, приведенном выше, нет колонны. Задача неразрешима? Отнюдь! Вместо колонны давайте построим стену, а сечение нарисуем сами.
1. Перейдите в окно плана этажа.
2. Активизируйте инструмент Arc/Circle (Дуга/окружность).
3. В точке пересечения окружности с одной из ее осей постройте окружность меньшего диаметра (рис. 8.36, а).
4. Используя операцию тиражирования объектов с вариантом Rotate (Поворот), размножьте малую окружность вдоль линии большого круга (рис. 8.36, б).
5. Активизируйте инструмент построения Wall (Стена), настройте необходимые параметры и выберите метод построения полигональной стены.
6. Включите магический жезл, нажав Пробел.
7. Удерживая нажатой клавишу Пробел, переместите указатель мыши внутрь контура, образованного полилинией. Указатель должен принять форму
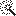
(рис. 8.36, в).
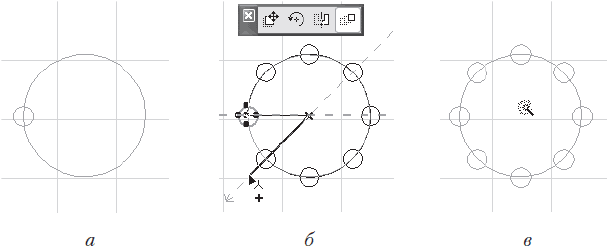
Рис. 8.36. Вспомогательные операции для построения колонны
8. Щелкните кнопкой мыши. Колонна построена.
9. Удалите полилинию и вспомогательные окружности (рис. 8.37, а).
10. Переключитесь в окно просмотра и редактирования трехмерных объектов и оцените результат построения (рис. 8.37, б).
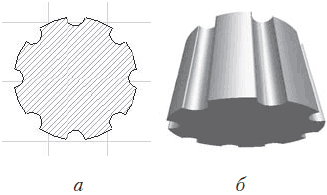
Рис. 8.37. Построение колонны с каннелюрами
Магический жезл может работать совместно с другими операциями редактирования объектов, причем с его помощью можно выполнять и операции логического вычитания объектов. Рассмотрим пример. Например, нужно создать сетку с квадратными ячейками.
1. Переключитесь в окно плана этажа.
2. С помощью инструмента Line (Линия) постройте квадрат, используя соответствующий метод.
3. Используя метод построения Matrix (Матрица), размножьте построенный объект с помощью операции Multiply (Тиражирование) (рис. 8.38, а).
4. Активизируйте инструмент Slab (Перекрытие).
5. Постройте прямоугольный контур перекрытия так, чтобы он перекрывал матрицу квадратов.
6. Выделите построенное перекрытие с помощью клавиши Shift.
Примечание
Использование клавиши Shift необходимо для того, чтобы не переключаться в режим выбора объектов, поскольку для работы магического жезла нужно находиться в режиме построения объекта.
7. Нажмите клавишу Пробел.
8. Не отпуская клавишу, поочередно перемещайте указатель мыши внутрь каждого квадрата и щелкайте кнопкой мыши (рис. 8.38, б).
9. По завершении указанных действий переключитесь в 3D-окно и оцените результат работы (рис. 8.38, в).
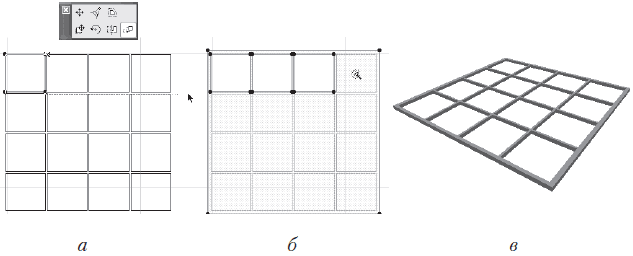
Рис. 8.38. Логическое вычитание с помощью магического жезла
При выполнении операции магический жезл сохраняет удаляемые объекты. Это легко проверить, если сдвинуть перекрытие в сторону. По данной причине, если есть необходимость вырезать отверстия и в то же время сохранить вырезанные контуры (а ими могут быть и трехмерные объекты), необходимо использовать именно магический жезл.
Рассмотрим еще один пример, показывающий возможности магического жезла. Допустим, имеется план парка с центральной клумбой и асфальтированными дорожками, расходящимися радиально от клумбы. Необходимо положить вокруг газонов бордюрный камень.
1. Используя известные вам инструменты создания и редактирования объектов, постройте перекрытия, которые будут изображать плоскость газонов (рис. 8.39, а).
2. Выберите инструмент создания балок и настройте параметры стандартной балки с прямоугольным сечением: высота – 500, ширина – 200.
3. Нажмите клавишу Пробел.
4. Не отпуская клавишу, последовательно щелкните кнопкой мыши внутри каждого контура. Все!
5. Переключитесь в 3D-окно и оцените результат построения (рис. 8.39, б).
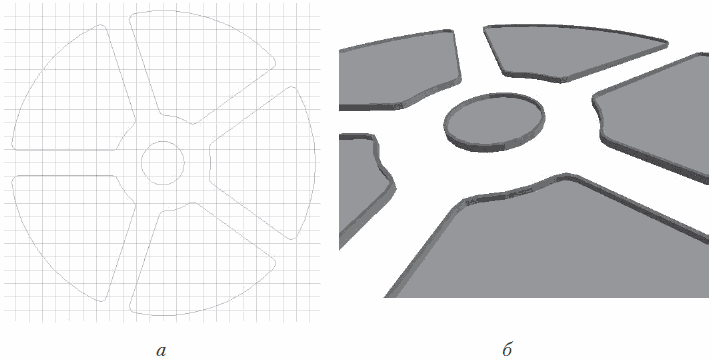
Рис. 8.39. Укладка бордюрного камня
Совет
Поупражняйтесь в использовании магического жезла в 2D– и 3D-окнах, используя в качестве контуров двумерные и трехмерные объекты, а также возможные комбинации их пересечений.