Числа с плавающей точкой    

Числа с плавающей точкой    

   Числа с плавающей точкой более или менее соответствуют тому, что математики называют "вещественными числами". Они включают в себя числа, расположенные между целыми. Вот некоторые из них: 2.75, 3.16Е7, 7.00 и 2е-8. Очевидно, что любое число с плавающей точкой можно записать несколькими способами. Более полное обсуждение "Е-нотации" будет проведено дальше, а мы только кратко поясним, что запись вида "3.16Е7" означает число, полученное в результате умножения 3.16 на 1,0 в седьмой степени, т. е. на 1 с семью нулями. Число 7 называется "порядком" (показателем степени при основании 10).

     Наиболее существенным моментом здесь является то, что способ кодирования, используемый для помещения в память числа с плавающей точкой, полностью отличается от аналогичной схемы для размещения целого числа. Формирование представления числа с плавающей точкой состоит в его разбиении на дробную часть и порядок; затем обе части раздельно помещаются в память. Поэтому число 7.00 из вышеприведенного списка нельзя поместить в память тем же способом, что и целое число 7, хотя оба имеют одно и то же значение. В десятичной записи (точно так же как и в двоичной) число "7.0" можно было бы записать в виде "0.7Е1"; тогда "0.7" будет дробной частью, а "1" - порядком. Для размещения чисел в памяти машины будут, конечно, использоваться двоичные числа и степени двойки вместо степеней десяти. Дополнительную информацию, относящуюся к этому вопросу, вы сможете найти в приложении Ж. Здесь же мы остановимся лишь на различиях, связанных с практическим использованием чисел этих двух типов.

     1. Целые числа не имеют дробной части, в то время как числа с плавающей точкой могут представлять как целые, так и дробные числа.

     2. Числа с плавающей точкой дают возможность представлять величины из более широкого диапазона, чем целые (см. табл. 3.1).

     3. При некоторых арифметических операциях, например при вычитании одного большого числа из другого, использование чисел с плавающей точкой приводит к большей потере точности.

     4. Операции над числами с плавающей точкой выполняются, как правило, медленнее, чем операции над целыми числами. Однако сейчас уже появились микропроцессоры, специально ориентированные на обработку чисел с плавающей точкой, и в них эти операции выполняются довольно быстро.

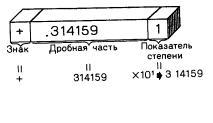
                                    РИС. 3.3. Десятичное представление числа p в формате с плавающей точкой.

     Возьмите некоторое число. Добавьте к нему 1, а затем вычтите из полученной суммы исходное число. Что у вас получится? У нас получилась 1. Но вычисления, производимые над числами с плавающей точкой, могут дать и совершенно неожиданный результат:

/*ошибка вычислений*/

main( )

{

   float a, b;

   b = 2.0е20 + 1.0;

   а = b - 2.0е20;

   printf(" %f ", a);

}

Результат равен

0000000

     Причина появления такого странного результата состоит в отсутствии доста точного числа разрядов для выполнения операций с требуемой точностью. Число 2.0е20 записывается как двойка с последующими двадцатью нулями, и, до бавляя к нему 1, мы пытаемся изменить 21-ю цифру Чтобы выполнить эту oпe рацию корректно, программа должна иметь возможность поместить в память число, состоящее из 21 цифры. Но число типа float (т е. с плавающей точкой) путем изменения порядка можно увеличить или уменьшить лишь на 6 или 7 цифр. Попытка вычисления оказалась неудачной. С другой стороны, если бы мы использовали, скажем, число 2.0е4 вместо 2.0е20, мы смогли бы получить правильный ответ, поскольку в этом случае мы пытались бы изменить 5-ю цифру, и точность представления чисел типа float оказалась бы вполне достаточной для этого.