8.4. Параметрический анализ как дополнительный к анализу переходных процессов
8.4. Параметрический анализ как дополнительный к анализу переходных процессов
Анализ переходных процессов (Transient Analysis) в сочетании с параметрическим анализом (Parametric Sweep) принадлежит к числу наиболее мощных инструментов, которые имеются в программе PSPICE. Однако вы будете удивлены тем, насколько легко его применять. Знаний, приобретенных вами к этому моменту, будет вполне достаточно, чтобы без особого труда освоить и анализ Transient Analysis + Parametric Sweep.
Напоминаем, что при проведении анализа Transient Analysis + Parametric Sweep вы не можете воспользоваться опциями Voltage Source и Current Source, находящимися в списке возможных переменных в окне Parametric. Эти изменяемые переменные предназначены только для параметрического анализа цепи постоянного тока DC Sweep + Parametric Sweep. Если вы намерены изменять в ходе анализа амплитуду, фазу, время задержки распространения сигнала, длительность фронта импульса или какую-либо другую характеристику источника тока или напряжения схемы, вы должны определить эти величины как Global Parameter и затем задать их изменение.
В качестве примера того, как проводится анализ Transient Analysis в сочетании с Parametric Sweep, исследуем переходную характеристику схемы LC_НЧ_фильтр, изображенной на рис. 8.18. Это задание вы уже выполняли в уроке 5. Но теперь, с использованием новых возможностей для анализа, решить задачу будет гораздо проще.
Шаг 26 Загрузите на экран SCHEMATICS схему RLC_MIX1.sch и замените установленный в ней источник напряжения типа VSIN на генератор импульсного напряжения типа VPULSE. Установите его атрибуты, руководствуясь образцом на рис. 8.20. Сохраните измененную схему в папке Projects под именем 12dB_IMP.sch.
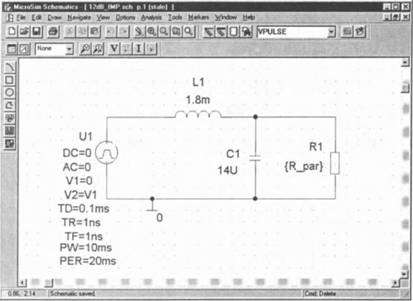
Рис. 8.20. LC_НЧ_фильтр с генератором импульсного напряжения типа VPULSE
Подготовьте основной анализ, то есть анализ переходных процессов, в окне Transient, как это показано на рис. 8.21.
Рис. 8.21. Предварительная установка анализа переходных процессов для исследования переходной характеристики схемы LC_НЧ_фильтр
Шаг 27 Подготовьте чертеж своей схемы к параметрическому анализу сопротивления R1 в соответствии с образцом на рис. 8.22.
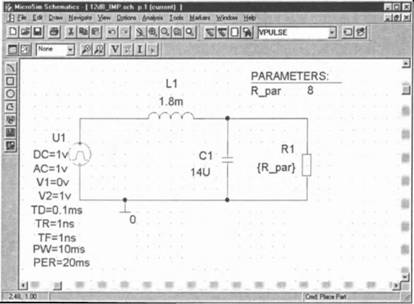
Рис. 8.22. Значение нагрузочного резистора как параметр для проведения анализа Transient
Шаг 28 Руководствуясь данными на рис. 8.23, проведите в окне Parametric предварительную установку параметрического анализа дополнительной переменной (сопротивление как глобальный параметр). Задайте изменение значения RH нагрузочного резистора R, от RH=4 Ом до RH=12 Ом с интервалами в 1 Ом.
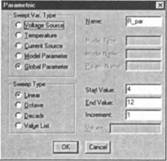
Рис. 8.23. Заданное изменение значения RH
Шаг 29 Установите в окне Analysis Setup флажки рядом с кнопками Transient… и Parametric…, как показано на рис. 8.24.
Рис. 8.24. Окно Analysis Setup с выставленными флажками Transient… и Parametric…
Шаг 30 Запустите процесс моделирования и выведите на экран PROBE диаграмму, изображенную на рис. 8.25.
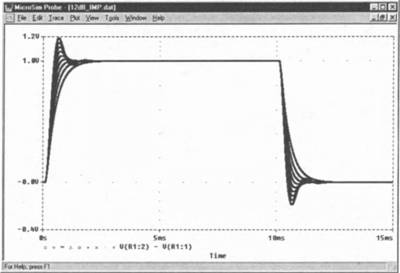
Рис. 8.25. Зависимость переходной характеристики схемы НЧ_фильтр от величины сопротивления
На диаграмме отчетливо видно, что фильтр оптимально, то есть наиболее быстро, работает только при одном единственном значении RH, и без выбросов достигает своего конечного состояния. Частотная характеристика фильтра также была оптимальной при одном единственном значении нагрузочного резистора (см. рис. 8.19), а именно для RH=8 Ом. Хочется надеяться, что значение сопротивления 8 Ом также окажется оптимальным и для переходной характеристики (импульсной характеристики).
Шаг 31 Увеличьте фрагмент диаграммы, изображённой на рис. 8.25, во фронтальной области импульса и определите значение сопротивления, при котором переходная характеристика фильтра является оптимальной (рис. 8.26).
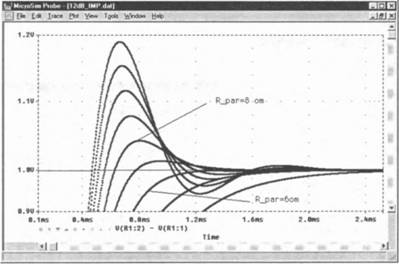
Рис. 8.26. Увеличенный фрагмент диаграммы
Увеличенный фрагмент диаграммы ясно показывает, что переходная характеристика данного фильтра является наиболее оптимальной при подключении к динамику с сопротивлением около 6 Ом.
Шаг 32 Увеличьте аналогичным образом другой фрагмент той же диаграммы, на этот раз в области затухания импульса, и убедитесь, что процесс затухания импульса данного фильтра является оптимальным также при значении сопротивления около 6 Ом.
Как выяснилось, частотная характеристика и импульсная характеристика частотных фильтров не оптимизируются одним и тем же значением сопротивления. Таким образом, вы вплотную столкнулись с центральной проблемой, возникающей при проектировании частотных фильтров: как найти компромисс между оптимальным процессом установления и затухания импульса и оптимальным разделением частоты. Частотные фильтры, сконструированные так, что их частотная характеристика оптимизирована за счет характеристики установления и затухания импульса, называют фильтрами с характеристикой Баттерворта. Частотные фильтры, переходная характеристика которых оптимизирована за счет частотной характеристики, называют фильтрами с характеристикой Бесселя.