13.1. Представление задач в виде И/ИЛИ-графов

13.1. Представление задач в виде И/ИЛИ-графов

В главах 11 и 12, говоря о решении задач, мы сконцентрировали свое внимание на пространстве состояний как средстве представления этих задач. В соответствии с таким подходом решение задач сводилось к поиску пути в графе пространства состояний. Однако для некоторых категорий задач представление в форме И/ИЛИ-графа является более естественным. Такое представление основано на разбиении задач на подзадачи. Разбиение на подзадачи дает преимущества в том случае, когда подзадачи взаимно независимы, а, следовательно, и решать их можно независимо друг от друга.

Проиллюстрируем это на примере. Рассмотрим задачу отыскания на карте дорог маршрута между двумя заданными городами, как показано на рис. 13.1. Не будем пока учитывать длину путей. Разумеется, эту задачу можно сформулировать как поиск пути в пространстве состояний. Соответствующее пространство состояний выглядело бы в точности, как карта рис. 13.1: вершины соответствуют городам, дуги — непосредственным связям между городами. Тем не менее давайте построим другое представление, основанное на естественном разбиении этой задачи на подзадачи.

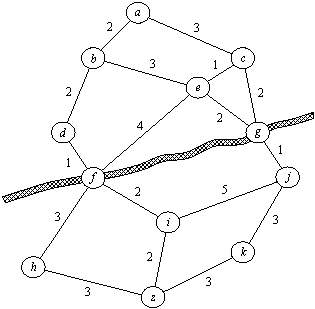
Рис. 13.1. Поиск маршрута из а в z на карте дорог. Через реку можно переправиться в городах f и g. И/ИЛИ-представление этой задачи показано на рис. 13.2.

На карте рис. 13.1 мы видим также реку. Допустим, что переправиться через нее можно только по двум мостам: один расположен в городе f, другой — в городе g. Очевидно, что искомый маршрут обязательно должен проходить через один из мостов, а значит, он должен пройти либо через f, либо через g. Таким образом, мы имеем две главных альтернативы:

Для того, чтобы найти путь из а в z, необходимо найти одно из двух:

(1) путь из а в z, проходящий через f, или

(2) путь из а в z, проходящий через  g.

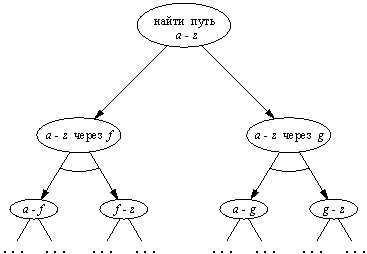
Рис. 13.2. И/ИЛИ-представление задачи поиска маршрута рис. 13.1. Вершины соответствуют задачам или подзадачам, полукруглые дуги означают, что все (точнее, обе) подзадачи должны быть решены.

Теперь каждую из этих двух альтернативных задач можно, в свою очередь, разбить следующим образом:

(1) Для того, чтобы найти путь из a в z через f, необходимо:

   1.1 найти путь из а и f  и

   1.2 найти путь из f в z.

(2) Для того, чтобы найти путь из a в z через g, необходимо:

   2.1 найти путь из а в g  и

   2.2 найти путь из g в z.

Рис. 13.3. (а) Решить P — это значит решить  P₁ или Р₂ или … (б) Решить Q — это значит решить все: Q₁ и Q₂ и ….

Итак, мы имеем две главных альтернативы для решения исходной задачи: (1) путь через f или (2) путь через g. Далее, каждую из этих альтернатив можно разбить на подзадачи (1.1 и 1.2 или 2.1 и 2.2 соответственно). Здесь важно то обстоятельство, что каждую из подзадач в обоих альтернативах можно решать независимо от другой. Полученное разбиение исходной задачи можно изобразить в форме И/ИЛИ-графа (рис. 13.2). Обратите внимание на полукруглые дуги, которые указывают на отношение И между соответствующими подзадачами. Граф, показанный на рис. 13.2 — это всего лишь верхняя часть всего И/ИЛИ-дерева. Дальнейшее разбиение подзадач можно было бы строить на основе введения дополнительных промежуточных городов.

Какие вершины  И/ИЛИ-графа  являются целевыми? Целевые вершины — это тривиальные, или "примитивные" задачи. В нашем примере такой подзадачей можно было бы считать подзадачу "найти путь из а в с", поскольку между городами а и с на карте имеется непосредственная связь.

Рассматривая наш пример, мы ввели ряд важных понятий. И/ИЛИ-граф — это направленный граф, вершины которого соответствуют задачам, а дуги — отношениям между задачами. Между дугами также существуют свои отношения. Это отношения И и ИЛИ, в зависимости от того, должны ли мы решить только одну из задач-преемников или же несколько из них (см. рис. 13.3). В принципе из вершины могут выходить дуги, находящиеся в отношении И вместе с дугами, находящимися в отношении ИЛИ. Тем не менее, мы будем предполагать, что каждая вершина имеет либо только И-преемников, либо только ИЛИ-преемников; дело в том, что в такую форму можно преобразовать любой И/ИЛИ граф, вводя в него при необходимости вспомогательные ИЛИ-вершины. Вершину, из которой выходят только И-дуги, называют И-вершиной; вершину, из которой выходят только ИЛИ-дуги, — ИЛИ-вершиной.

Когда задача представлялась в форме пространства состояний, ее решением был путь в этом пространстве. Что является решением в случае И/ИЛИ-представления? Решение должно, конечно, включать в себя все подзадачи И-вершины. Следовательно, это уже не путь, а дерево. Такое решающее дерево T определяется следующим образом:

• исходная задача P — это корень дерева T;

• если P является ИЛИ-вершиной, то в T содержится только один из ее преемников (из И/ИЛИ-графа) вместе со своим собственным решающим деревом;

• если P — это И-вершина, то все ее преемники (из И/ИЛИ-графа) вместе со своими решающими деревьями содержатся в T.

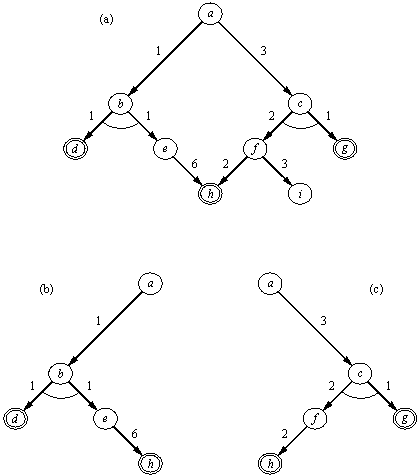
Рис. 13.4. (а) Пример И/ИЛИ-графа: d, g и h — целевые вершины; a — исходная задача. (b) и (с) Два решающих дерева, стоимости которых равны 9 и 8 соответственно. Здесь стоимость решающего дерева определена как сумма стоимостей всех входящих в него дуг.

Иллюстрацией к этому определению может служить рис. 13.4. Используя стоимости, мы можем формулировать критерии оптимальности решения. Например, можно определить стоимость решающего графа как сумму стоимостей всех входящих в него дуг. Тогда, поскольку обычно мы заинтересованы в минимизации стоимости, мы отдадим предпочтение решающему графу, изображенному на рис. 13.4(с).

Однако мы не обязательно должны измерять степень оптимальности решения, базируясь на стоимостях дуг. Иногда более естественным окажется приписывать стоимость не дугам, а вершинам, или же и тем, и другим одновременно.

Подведем итоги:

• И/ИЛИ-представление основано на философии сведения задач к подзадачам.

• Вершины И/ИЛИ-графа соответствуют задачам; связи между вершинами — отношениям между задачами.

• Вершина, из которой выходят ИЛИ-связи, называется ИЛИ-вершиной. Для того, чтобы решить соответствующую задачу, нужно решить одну из ее задач-преемников.

• Вершина, из которой выходят И-связи, называется И-вершиной. Для того, чтобы решить соответствующую задачу, нужно решить все ее задачи-преемники.

• При заданном И/ИЛИ-графе конкретная задача специфицируется заданием

  стартовой вершины и

  целевого условия для распознавания

  целевых вершин.

• Целевые вершины (или "терминальные вершины") соответствуют тривиальным (или "примитивным") задачам.

• Решение представляется в виде решающего графа — подграфа всего И/ИЛИ-графа.

• Представление задач в форме пространства состояний можно рассматривать как специальный частный случай И/ИЛИ-представления, когда все вершины И/ИЛИ-графа являются ИЛИ-вершинами.

• И/ИЛИ-представление имеет преимущество в том случае, когда вершинами, находящимися в отношении И, представлены подзадачи, которые можно решать независимо друг от друга. Критерий независимости можно несколько ослабить, а именно потребовать, чтобы существовал такой порядок решения И-задач, при котором решение более "ранних" подзадач не разрушалось бы при решении более "поздних" под задач.

• Дугам или вершинам, или и тем, и другим можно приписать стоимости с целью получить возможность сформулировать критерий оптимальности решения.