9.1.2. Сортировка списков

9.1.2. Сортировка списков

Сортировка применяется очень часто. Список можно отсортировать (упорядочить), если между его элементами определено отношение порядка. Для удобства изложения мы будем использовать отношение порядка

больше( X, Y)

означающее, что X больше, чем Y, независимо от того, что мы в действительности понимаем под "больше, чем". Если элементами списка являются числа, то отношение больше будет, вероятно, определено как

больше( X, Y) :- X > Y.

Если же элементы списка — атомы, то отношение больше может соответствовать алфавитному порядку между ними.

Пусть

сорт( Спис, УпорСпис)

обозначает отношение, в котором Спис — некоторый список, а УпорСпис — это список, составленный из тех же элементов, но упорядоченный по возрастанию в соответствия с отношением больше. Мы построим три определения этого отношения на Прологе, основанные на трех различных идеях о механизме сортировки. Вот первая идея:

Для того, чтобы упорядочить список Спис, необходимо:

• Найти в Спис два смежных элемента X и Y, таких, что больше( X, Y), и поменять X и Y местами, получив тем самым новый список Спис1; затем отсортировать Спис1.

• Если в Спис нет ни одной пары смежных элементов X и Y, таких, что больше( X, Y), то считать, что Спис уже отсортирован.

Мы переставили местами 2 элемента X и Y, расположенные в списке "не в том порядке", с целью приблизить список к своему упорядоченному состоянию. Имеется в виду, что после достаточно большого числа перестановок все элементы списка будут расположены в правильном порядке. Описанный принцип сортировки принято называть методом пузырька, поэтому соответствующая прологовская процедура будет называться пузырек.

пузырек( Спис, УпорСпис) :-

 перест( Спис, Спис1), !, % Полезная перестановка?

 пузырек( Спис1, УпорСпис).

пузырек( УпорСпис, УпорСпис).

  % Если нет, то список уже упорядочен

перест( [X, Y | Остаток], [Y, X ) Остаток] ):-

 % Перестановка первых двух элементов

 больше( X, Y).

перест( [Z | Остаток], [Z | Остаток1] ):-

 перест( Остаток, Остаток1). % Перестановка в хвосте

Еще один простой алгоритм сортировки называется сортировкой со вставками. Он основан на следующей идее:

Для того, чтобы упорядочить непустой список L = [X | Хв], необходимо:

(1) Упорядочить хвост Хв списка  L.

(2) Вставить голову X списка L в упорядоченный хвост, поместив ее в такое место, чтобы получившийся список остался упорядоченным. Список отсортирован.

Этот алгоритм транслируется в следующую процедуру вставсорт на Прологе:

вставсорт([], []).

вставсорт( [X | Хв], УпорСпис) :-

 вставсорт( Хв, УпорХв), % Сортировка хвоста

встав( X, УпорХв, УпорСпис).

  % Вставить X на нужное место

встав( X, [Y | УпорСпис], [Y | УпорСпис1]):-

 больше( X, Y), !,

 встав( X, УпорСпис, УпорСпис1).

встав( X, УпорСпис, [X | УпорСпис] ).

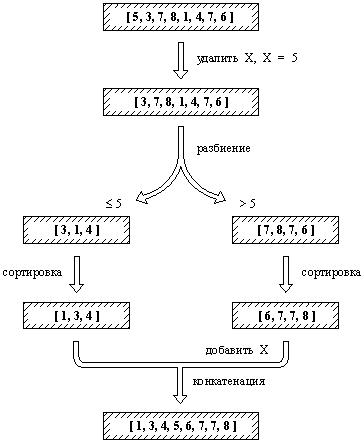
Рис. 9.1. Сортировка списка процедурой быстрсорт.

Процедуры сортировки пузырек и вставсорт просты, но не эффективны. Из этих двух процедур процедура со вставками более эффективна, однако среднее время, необходимое для сортировки списка длиной  n  процедурой вставсорт, возрастает с ростом n пропорционально n?. Поэтому для длинных списков значительно лучше работает алгоритм быстрой сортировки, основанный на следующей идее (рис. 9.1):

Для того, чтобы упорядочить непустой список L,  необходимо:

(1) Удалить из списка L какой-нибудь элемент X и разбить оставшуюся часть на два списка, называемые Меньш и Больш, следующим образом: все элементы большие, чем X, принадлежат списку Больш, остальные — списку Меньш.

(2) Отсортировать список Меньш, результат — список УпорМеньш.

(3) Отсортировать список Больш, результат — список УпорБольш.

(4) Получить результирующий упорядоченный список как конкатенацию списков УпорМеньш и [ X | УпорБольш].

Заметим, что если исходный список пуст, то результатом сортировки также будет пустой список. Реализация быстрой сортировки на Прологе показана на рис. 9.2. Здесь в качестве элемента X, удаляемого из списка, всегда выбирается просто голова этого списка. Разбиение на два списка запрограммировано как отношение с четырьмя аргументами:

разбиение( X, L, Больш, Меньш).

Временная сложность нашего алгоритма зависит от того, насколько нам повезет при разбиении сортируемого списка. Если списки всегда разбиваются на два списка примерно равной длины, то процедура сортировки имеет временную сложность порядка n log n, где n — длина исходного списка. Если же, наоборот, разбиение всегда приводит к тому, что один из списков оказывается значительно больше другого, то сложность будет порядка  n?. Анализ показывает, что, к счастью, средняя производительность быстрой сортировки ближе к лучшему случаю, чем к худшему.

Программу, показанную на рис. 9.2, можно усовершенствовать, если реализовать операцию конкатенации более эффективно. Напомним, что конкатенация становится тривиальной операцией после применения разностного представления списков, введенного в гл. 8. Для того, чтобы использовать эту идею в нашей процедуре сортировки, нужно представить встречающиеся в ней списки в форме пар вида A-Z следующим образом:

 УпорМеньш имеет вид A1-Z1

 УпорБольш имеет вид A2-Z2

быстрсорт( [], [] ).

быстрсорт( [X | Хвост], УпорСпис) :-

 разбиение( X, Хвост, Меньш, Больш),

 быстрсорт( Меньш, УпорМеньш),

 быстрсорт( Больш, УпорБольш),

 конк( УпорМеньш, [X | УпорБольш], УпорСпис).

разбиение( X, [], [], [] ).

разбиение( X, [Y | Хвост], [Y | Меньш], Больш ) :-

 больше( X, Y), !,

 разбиение( X, Хвост, Меньш, Больш).

разбиение( X, [Y | Хвост], Меньш, [Y | Больш] ) :-

 разбиение( X, Хвост, Меньш, Больш).

конк( [], L, L).

конк( [X | L1], L2, [X | L3] ) :-

 конк( L1, L2, L3 ).

Рис. 9.2. Быстрая сортировка.

Тогда конкатенации списков

УпорМеньш и [ X | УпорБольш]

будет соответствовать конкатенация пар

A1-Z1 и [ X | A2]-Z2

В результате мы получим

А1-Z2, причем Z1 = [ X | А2]

Пустой список представляется парой Z-Z. Систематически вводя изменения в программу рис. 9.2, мы получим более эффективный способ реализации процедуры быстрсорт, показанный на рис. 9.3 под именем быстрсорт2. Здесь, как и раньше, процедура быстрсорт использует обычное представление списков, но в действительности сортировку выполняет более эффективная процедура быстрсорт2, использующая разностное представление. Эти две процедуры связаны между собой, соотношением

быстрсорт( L, S) :-

 быстрсорт2( L, S-[] ).

быстрсорт( Спис, УпорСпис) :-

 быстрсорт2( Спис, УпорСпис-[] ).

быстрсорт2( [], Z-Z).

быстрсорт2( [X | Хвост], A1-Z2) :-

 разбиение( X, Хвост, Меньш, Больш),

 быстрсорт2( Меньш, А1-[X | A2] ),

 быстрсорт2( Больш, A2-Z2).

Рис. 9.3. Более эффективная реализация процедуры быстрсортс использованием разностного представления списков. Отношение разбиение( X, Спис, Меньш, Больш) определено, как на рис. 9.2.

Упражнения

9.5. Напишите процедуру слияния двух упорядоченных списков в один третий список. Например:

?- слить( [2, 5, 6, 6, 8], [1, 3, 5, 9], L).

L = [1, 2, 3, 5, 5, 6, 6, 8, 9]

9.6. Программы сортировки, показанные на рис. 9.2 и 9.3, отличаются друг от друга способом представления списков. Первая из них использует обычное представление, в то время как вторая — разностное представление. Преобразование из одного представления в другое очевидно и может быть автоматизировано. Введите в программу рис. 9.2 необходимые изменения, чтобы преобразовать ее в программу рис. 9.3.

9.7. Наша программа быстрсорт в случае, когда исходный список уже упорядочен или почти упорядочен, работает очень неэффективно. Проанализируйте причины этого явления.

9.8. Существует еще одна хорошая идея относительно механизма сортировки списков, позволяющая избавиться от недостатков программы быстрсорт, а именно: разбить список на два меньших списка, отсортировать их, а затем слить вместе. Итак, для того, чтобы отсортировать список L, необходимо

• разбить L на два списка L1 и L2 примерно одинаковой длины;

• произвести сортировку списков L1 и L2,получив списки S1 и S2;

• слить списки S1 и S2, завершив на этом сортировку списка L.

Реализуйте этот принцип сортировки и сравните его эффективность с эффективностью программы быстрсорт.