9.5.2. Поиск пути в графе

9.5.2. Поиск пути в графе

Пусть G — граф, а А и Z — две его вершины. Определим отношение

путь( А, Z, G, P)

где P — ациклический путь между А и Z в графе G. Если G — граф, показанный в левой части рис. 9.18, то верно:

путь( a, d, G, [a, b, d] )

путь( а, d, G, [a, b, c, d] )

Поскольку путь не должен содержать циклов, любая вершина может присутствовать в пути не более одного раза. Вот один из методов поиска пути:

Для того, чтобы найти ациклический путь P между А и Z в графе G, необходимо:

Если А = Z , то положить P = [А], иначе найти ациклический путь P1 из произвольной вершины Y в Z, а затем найти путь из А в Y, не содержащий вершин из P1.

В этой формулировке неявно предполагается, что существует еще одно отношение, соответствующее поиску пути со следующий ограничением: путь не должен проходить через вершины из некоторого подмножества (в данном случае P1) множества всех вершин графа. В связи с этим мы определим ещё одну процедуру:

путь1( А, P1, G, P)

Аргументы в соответствии с рис. 9.19 имеют следующий смысл:

• А — некоторая вершина,

• G — граф,

• P1 — путь в G,

• P — ациклический путь в G, идущий из А в начальную вершину пути P1, а затем — вдоль пути P1 вплоть до его конца.

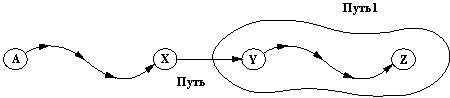
Pис. 9.19. Отношение путь1: Путь — это путь между А и Z, в своей заключительной части он перекрывается с Путь1.

Между путь и путь1 имеется следующее соотношение:

путь( А, Z, G, P) :- путь1( А, [Z], G, P).

На рис. 9.19 показана идея рекурсивного определения отношения путь1. Существует "граничный" случай, когда начальная вершина пути P1 (Y на рис. 9.19) совпадает с начальной вершиной А пути P. Если же начальные вершины этих двух путей не совпадают, то должна существовать такая вершина X, что

(1) Y — вершина, смежная с X,

(2) X не содержится в P1 и

(3) для P выполняется отношение путь1( А, [X | P1], G, P).

путь( A, Z, Граф, Путь) :-

 путь1( А, [Z], Граф, Путь).

путь1( А, [А | Путь1, _, [А | Путь1] ).

путь1( А, [Y | Путь1], Граф, Путь) :-

 смеж( X, Y, Граф),

 принадлежит( X, Путь1), % Условие отсутствия цикла

 путь1( А, [ X, Y | Путь1], Граф, Путь).

Рис. 9.20. Поиск в графе Граф ациклического пути Путь из А в Z.

На рис. 9.20 программа показана полностью. Здесь принадлежит — отношение принадлежности элемента списку. Отношение

смеж( X, Y, G)

означает, что в графе G существует дуга, ведущая из X в Y. Определение этого отношения зависит от способа представления графа. Если G представлен как пара множеств (вершин и ребер)

G = граф( Верш, Реб)

то

смеж( X, Y, граф( Верш, Реб) ) :-

 принадлежит( p( X, Y), Реб);

 принадлежит( p( Y, X), Реб).

Классическая задача на графах — поиск Гамильтонова цикла, т.е. ациклического пути, проходящего через все вершины графа. Используя отношение путь, эту задачу можно решить так:

гамильтон( Граф, Путь) :-

 путь( _, _, Граф, Путь),

 всевершины( Путь, Граф).

всевершины( Путь, Граф) :-

 not (вершина( В, Граф),

 not принадлежит( В, Путь) ).

Здесь вершина( В, Граф) означает: В — вершина графа Граф.

Каждому пути можно приписать его стоимость. Стоимость пути равна сумме стоимостей входящих в него дуг. Если дугам не приписаны стоимости, то тогда, вместо стоимости, говорят о длине пути.

Для того, чтобы наши отношения путь и путь1 могли работать со стоимостями, их нужно модифицировать, введя дополнительный аргумент для каждого пути:

путь( А, Z, G, P, С)

путь1( A, P1, C1, G, P, С)

Здесь С — стоимость пути P, a C1 — стоимость пути P1. В отношении смеж также появится дополнительный аргумент, стоимость дуги. На рис. 9.21 показана программа поиска пути, которая строит путь и вычисляет его стоимость.

путь( А, Z, Граф, Путь, Ст) :-

 путь1( A, [Z], 0, Граф, Путь, Ст).

путь1( А, [А | Путь1], Ст1, Граф, [А | Путь1], Ст).

путь1( А, [Y | Путь1], Ст1, Граф, Путь, Ст) :-

 смеж( X, Y, СтXY, Граф),

 not принадлежит( X, Путь1),

 Ст2 is Ст1 + СтXY,

 путь1( А, [ X, Y | Путь1], Ст2, Граф, Путь, Ст).

Рис. 9.21. Поиск пути в графе: Путь — путь между А и Z в графе Граф стоимостью Ст.

Эту процедуру можно использовать для нахождения пути минимальной стоимости. Мы можем построить путь минимальной стоимости между вершинами Верш1, Верш2 графа Граф, задав цели

путь( Bepш1, Верш2, Граф, МинПуть, МинСт),

 not( путь( Верш1, Верш2, Граф, _, Ст), Ст<МинСт )

Аналогично можно среди всех путей между вершинами графа найти путь максимальной стоимости, задав цели

путь( _, _, Граф, МаксПуть, МаксСт),

 not( путь( _, _, Граф, _, Ст), Ст > МаксСт)

Заметим, что приведенный способ поиска максимальных и минимальных путей крайне неэффективен, так как он предполагает просмотр всех возможных путей и потому не подходит для больших графов из-за своей высокой временной сложности. В искусственном интеллекте задача поиска пути возникает довольно часто. В главах 11 и 12 мы изучим более сложные методы нахождения оптимальных путей.