10.2. AVL-дерево: приближенно сбалансированное дерево
10.2. AVL-дерево: приближенно сбалансированное дерево
AVL-дерево — это дерево, обладающее следующими свойствами:
(1) Левое и правое поддеревья отличаются по глубине не более чем на 1.
(2) Оба поддерева являются AVL-деревьями.
Деревья, удовлетворяющие этому определению, могут быть слегка разбалансированными. Однако можно показать, что даже в худшем случае глубина AVL-дерева примерно пропорциональна log n, где n — число вершин дерева. Таким образом гарантируется логарифмический порядок производительности операций внутри, добавить и удалить.
Операции над AVL-деревом работают по существу так же, как и над двоичным справочником. В них только сделаны добавления, связанные с поддержанием приближенной сбалансированности дерева. Если после вставления или удаления дерево перестает быть приближенно сбалансированным, то специальные механизмы возвращают ему требуемую степень сбалансированности. Для того, чтобы эффективно реализовать этот механизм, нам придется сохранять некоторую дополнительную информацию относительно степени сбалансированности дерева. На самом деле, нам нужно знать только разность между глубинами поддеревьев, которая может принимать значения -1, 0 или +1. Тем не менее для простоты мы предпочтем сохранять сами величины глубин поддеревьев, а не разности между ними.
Мы определим отношение вставления элемента как
доб_avl( Дер, X, НовДер)
где оба дерева Дер и НовДер — это AVL-деревья, причем НовДер получено из Дер вставлением элемента X. AVL-деревья будем представлять как термы вида
д( Лев, А, Прав)/Глуб
где А — корень, Лев и Прав — поддеревья, а Глуб — глубина дерева. Пустое дерево изображается как nil/0. Теперь рассмотрим вставление элемента X в непустой AVL-справочник
Дер = д( L, A, R)/H
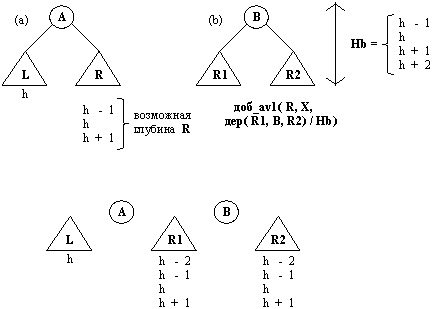
Рис. 10.8. Задача вставления элемента в AVL-справочник (a) AVL-дерево перед вставлением X, X > А; (b) AVL-дерево после вставления X в R; (с) составные части, из которых следует построить новое дерево.
Начнем со случая, когда X больше А. X необходимо вставить в R, поэтому имеем следующее отношение:
доб_аv1( R, X, д( R1, В, R2)/Hb)
На рис. 10.8 показаны составные части, из которых строится дерево НовДер:
L, А, R1, В, R2
Какова глубина деревьев L, R, R1 и R2? L и R могут отличаться по глубине не более, чем на 1. На рис. 10.8 видно, какую глубину могут иметь R1 и R2. Поскольку в R был добавлен только один элемент X, только одно из поддеревьев R1, R2 может иметь глубину h+1.
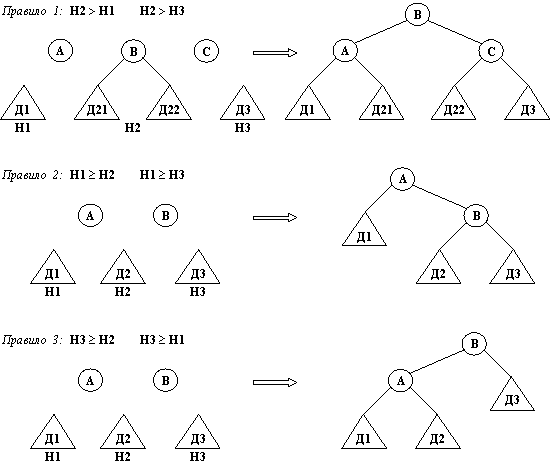
Рис. 10.9. Три правила построения нового AVL-дepевa.
В случае, когда X меньше, чем А, имеем аналогичную ситуацию, причем левое и правое поддеревья меняются местами. Таким образом, в любом случае мы должны построить дерево НовДер, используя три дерева (назовем их Дер1, Дер2 и Дер3) и два отдельных элемента А и В. Теперь рассмотрим вопрос: как соединить между собой эти пять составных частей, чтобы дерево НовДер было AVL-справочником? Ясно, что они должны располагаться внутри НовДер в следующем порядке (слева направо):
Дер1, А, Дер2, В, Дер3
Рассмотрим три случая:
(1) Среднее дерево Дер2 глубже остальных двух деревьев.
(2) Дер1 имеет глубину не меньше, чем Дер2 и Дер3.
(3) Дер3 имеет глубину не меньше, чем Дер2 и Дер1.
На рис. 10.9 видно, как можно построить дерево НовДер в каждом из этих трех случаев. Например, в случае 1 среднее дерево Дер2 следует разбить на два части, а затем включить их в состав НовДер. Три правила, показанные на pис.10.9, нетрудно запасать на Прологе в виде отношения
соединить( Дер, А, Дер2, В, Дер3, НовДер)
Последний аргумент НовДер — это AVL-дерево, построенное из пяти составных частей, пяти первых аргументов. Правило 1, например, принимает вид:
соединить( Д1/Н1, А, д( Д21, В, Д22)/Н2, С, Д3/Н3,
% Пять частей
д( д( Д1/Н1, А, Д21)/На, В, д( Д22, С, Д3/Н3)/Нс)/Нb) :-
% Результат
H2 > H1, H2 > Н3, % Среднее дерево глубже остальных
На is Н1 + 1, % Глубина левого поддерева
Нс is Н3 + 1, % Глубина правого поддерева
Hb is На + 1, % Глубина всего дерева
Программа доб_аvl, вычисляющая также глубину дерева и его поддеревьев, показана полностью на рис. 10.10.
Упражнение
10.3. Определите отношение
avl( Дер)
для проверки того, является ли Дер AVL-деревом, т.е. верно ли, что любые два его поддерева, подсоединенные к одной и той же вершине, отличаются по глубине не более чем на 1. Двоичные деревья представляйте в виде термов д( Лев, Кор, Прав) или nil.
% Вставление элемента в AVL-справочник
доб_аvl( nil/0, X, д( nil/0, X, nil/0)/1).
% Добавить X к пустому дереву
доб_аvl( д( L, Y, R)/Ну, X, НовДер) :-
% Добавить X к непустому дереву
больше( Y, X),
доб_аvl( L, X, д( L1, Z, L2)/ _ ),
% Добавить к левому поддереву
соединить( L1, Z, L2, Y, R, НовДер).
% Сформировать новое дерево
доб_avl( д( L, Y, R)/Ну, X, НовДер) :-
больше( X, Y),
доб_avl( R, X, д( R1, Z, R2)/ _ ),
% Добавить к правому поддереву
соединить( L1, Y, Rl, Z, R2, НовДер).
соединить( Д1/Н1, А, д( Д21, В, Д22)/Н2, С, Д3/Н3,
д( д( Д1/Н1, А, Д21)/На, В, д( Д22, С, L3/Н3)/Нс)/Нb) :-
Н2 > H1, H2 > Н3, % Среднее дерево глубже остальных
На is H1 + 1,
Hс is Н3 + 1,
Нb is На + 1.
соединить( Д1/Н1, А, д( Д2/Н2, С, Д3/Н3,
д( Д1/Н1, А, д( Д2/Н2, С, Д3/Н3)/Нс)/На) :-
H1 >= H2, H1 >= Н3, % "Глубокое" левое дерево
max1( H2, Н3, Нс),
max1( H1, Нс, На).
соединить( Д1/Н1, А, Д2/Н2, С, Д3/Н3,
д( д( Д1/Н1, А, Д2/Н2)/На, С, Д3/Н3)/Нс) :-
Н3 >= H2, Н3 >= H1, % "Глубокое" правое дерево
max1( H1, H2, На),
max1( На, Н3, Нс).
max1( U, V, М) :-
U > V, !, М is U + 1; % М равно 1 плюс max( U, V)
М is V + 1.
Рис. 10.10. Вставление элемента в AVL-справочник. В этой программе предусмотрено, что попытка повторного вставления элемента терпит неудачу. По поводу процедуры соединить см. рис. 10.9.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
14.4.3. Ввод элемента в дерево: tsearch()
14.4.3. Ввод элемента в дерево: tsearch() Эти процедуры выделяют память для вершин дерева. Для их использования с несколькими деревьями нужно предоставить им указатель на переменную void*, в которую они заносят адрес корневой вершины. При создании нового дерева инициализируйте
Дерево исходных кодов ядра
Дерево исходных кодов ядра Дерево исходных кодов ядра содержит ряд каталогов, большинство из которых также содержит подкаталоги. Каталоги, которые находятся в корне дерева исходных кодов, и их описание приведены в табл. 2.1.Таблица 2.1. Каталоги в корне дерева исходных
Дерево семейства процессов
Дерево семейства процессов В операционной системе Linux существует четкая иерархия процессов. Все процессы являются потомками процесса init, значение идентификатора PID для которого равно 1. Ядро запускает процесс init на последнем шаге процедуры загрузки системы. Процесс init, в
Базисное дерево
Базисное дерево Так как ядро должно проверять наличие страниц в страничном кэше перед тем, как запускать любую операцию страничного ввода-вывода, то этот поиск должен выполняться быстро. В противном случае затраты на поиск могут свести на нет все выгоды кэширования (по
Семантическое DOM-дерево
Семантическое DOM-дерево Логическим продолжением уже проведенных исследований CSS/DOM-производительности браузеров стало рассмотрение зависимости времени создания документа от числа тегов (узлов дерева). Раздельно были проанализированы случаи, когда DOM-дерево является
Глава 5 Дерево каталогов Linux
Глава 5 Дерево каталогов Linux Эта глава полностью посвящена структуре и размещению каталогов и файлов в Linux. Поскольку для различных дистрибутивов структура может слегка отличаться, для определенности будем рассматривать дистрибутив Red Hat 7.1.Для того чтобы ориентироваться
4.1. Файлы и каталоги. Дерево каталогов
4.1. Файлы и каталоги. Дерево каталогов В свое время, при использовании DOS вводилось определение файла как поименованной области данных на диске — на то DOS и дисковая операционная система. В Linux понятие файла значительно расширено. Практически все, с чем вы имеете дело в Linux,
5.6 Всемирное дерево имен
5.6 Всемирное дерево имен Имена Интернета структурированы как дерево (см. рис. 5.1). Каждому узлу дерева присвоена метка. Каждый узел дерева имеет имя, называемое именем домена (domain name). Имя домена для узла создается из меток, проходимых по пути от этого узла до вершины дерева.
20.5.1 Дерево SMI
20.5.1 Дерево SMI Вспомним, что первоначально SNMP предполагался как временное решение до выпуска стандартов управления ISO. На рис. 20.4 дерево администрирования/именования отражает первичные попытки согласования с ISO. Рис. 20.4. Дерево администрирования и именования SMIУзлы вверху
Wood (Дерево)
Wood (Дерево) Текстура дерева имеет большое значение при разработке дизайна. Рисунок поверхности среза дерева часто используется для декорирования объектов интерьера. Рисунок дерева наносится на предметы мебели, сделанные из ДСП, пластика и других материалов, бытовую
Дерево модели
Дерево модели Древовидное представление трехмерной модели (сборки или детали) в девятой версии претерпело значительные изменения. В частности, была добавлена возможность представления состава модели в виде структурированных разделов (рис. 1.72, а). При этом элементы
Вставка в красно-черное дерево
Вставка в красно-черное дерево Теперь, когда мы ознакомились с правилами, определяющими структуру красно-черного дерева, возникает вопрос, как их использовать для вставки нового узла в красно-черное дерево? Начнем со знакомой операции, и выполним поиск узла. Если он будет
Сортирующее дерево
Сортирующее дерево Классическая структура данных, используемая для создания очереди по приоритету, известна под названием сортирующего дерева (или "кучи"). Сортирующее дерево (heap), на которое еще ссылаются как на частично упорядоченное полное двоичное дерево, - это
Вставка в сортирующее дерево
Вставка в сортирующее дерево Рассмотрим алгоритмы вставки и удаления. Вначале ознакомимся со вставкой. Чтобы вставить элемент в сортирующее дерево, мы добавляем его в конец этого дерева, в единственную позицию, которая соответствует требованию полноты (на рис. 5 этой
2.6. Дерево модели
2.6. Дерево модели Дерево построения документа — структурированный список («дерево») объектов, отражающий последовательность создания документа. Отображение значка «+» рядом с объектом означает, что он имеет подчиненные объекты. Чтобы развернуть их список, щелкните
РЫНКИ: Убей дерево
РЫНКИ: Убей дерево Автор: Владимир ГуриевВ сентябре 2006 года стало известно сразу о нескольких инициативах крупных компаний на рынке электронных книг. Sony объявила о выходе Sony Reader и открытии магазина цифровых книг. Panasonic показал прототип своей электронной книги с цветным