3.2.5. Подсписок

Рассмотрим теперь отношение подсписок. Это отношение имеет два аргумента — список L и список S, такой, что S содержится в L в качестве подсписка. Так отношение

подсписок( [c, d, e], [a, b, c, d, e, f] )

имеет место, а отношение

подсписок( [c, e], [a, b, c, d, e, f] )

нет. Пролог-программа для отношения подсписок может основываться на той же идее, что и принадлежит1, только на этот раз отношение более общо (см. рис. 3.4).

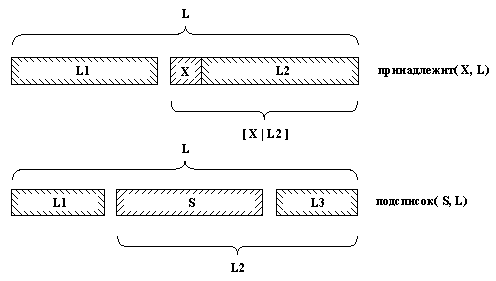
Рис. 3.4. Отношения принадлежит и подсписок.

Его можно сформулировать так:

S является подсписком L, если

(1) L можно разбить на два списка L1 и L2 и

(2) L2 можно разбить на два списка S и L3.

Как мы видели раньше, отношение конк можно использовать для разбиения списков. Поэтому вышеприведенную формулировку можно выразить на Прологе так:

подсписок( S, L) :-

конк( L1, L2, L),

конк( S, L3, L2).

Ясно, что процедуру подсписок можно гибко использовать различными способами. Хотя она предназначалась для проверки, является ли какой-либо список подсписком другого, ее можно использовать, например, для нахождения всех подсписков данного списка:

?- подсписок( S, [а, b, с] ).

S = [];

S = [a];

S = [а, b];

S = [а, b, с];

S = [b];

...