Результаты выполнения тестов

Результаты выполнения тестов

В разделе сопровождающих эту книгу материалов, который расположен на Web-сайте издательства, можно найти тестовую программу, которая применяет все рассмотренные нами тесты к стандартному генератору случайных чисел Delphi и минимальному стандартному генератору случайных чисел. На рис. 6.1 приведены результаты проведения одного из тестов для генератора случайных чисел Delphi.

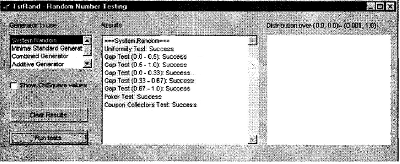
Рисунок. 6.1. Тестирование стандартного генератора Delphi

Как видите, данный конкретный тест свидетельствует о том, что стандартный генератор Delphi успешно прошел проверку. (под успешным прохождением теста понимается, что предложенная к тестированию последовательность случайных чисел не дает результатов, которые являются значимыми на уровне 5%.)

Окно в правой части окна программы представляет собой снимок случайных чисел, полученных на выходе генератора. Координаты точек вычисляются на основе двух случайных чисел: первого для оси х, а второго - для оси Y. После этого точки выводятся в окне, если они находятся в прямоугольнике (0.0, 0.0, 0.001, 1.0) или, другими словами, в прямоугольнике, нижний левый угол которого расположен в точке (0.0, 0.0), а верхний правый - в точке (0.001, 1.0). Чтобы распределение точек было удобнее изучать, прямоугольник растянут по оси х. Как видите, на рисунке точки случайным образом разбросаны по всему прямоугольнику. Никакой системы при этом не наблюдается.

У вас может возникнуть удивление, зачем мы так много говорим об этом окне. Посмотрите на рис. 6.2, на котором показана та же программа, но для минимального стандартного генератора случайных чисел. Как видите, и этот генератор успешно прошел все тесты, но посмотрите на распределение случайных точек. Очевидно, что генератор дает последовательность случайных чисел, которые при переносе их на график формируют определенный регулярный рисунок.

Регулярность минимального стандартного генератора не позволяет использовать его для некоторых приложений, особенно тех, которые требуют пар случайных чисел. Даже незначительной регулярности бывает достаточно для того, чтобы приложение давало неверные результаты. Кроме того, отсутствие регулярности в результатах стандартного генератора случайных чисел Delphi в двухмерной плоскости не означает, что регулярности не будет в гиперплоскостях более высокой размерности. Существуют тесты, которые проверяют случайные числа на наличие регулярности в А> мерном пространстве, но давайте не будем погружаться в изучение слишком сложных тестов, а рассмотрим методы использования двух уже известных нам генераторов для дальнейшей рандомизации их выходных данных.

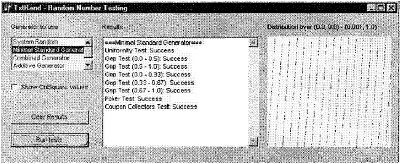
Рисунок 6.2. Тестирование минимального стандартного генератора

Мы рассмотрим три метода: первый известен как комбинаторный, второй - аддитивный и третий - метод тасования.

Комбинирование генераторов

Комбинирование генераторов заключается в параллельном использовании двух (или большего количества) мультипликативных линейных конгруэнтных генераторов с различными длинами циклов. Случайные числа генерируются обоими генераторами, а затем вычисляется их разность. Если получено отрицательное число, необходимо сделать его положительным, сложив его с длиной цикла первого генератора.

Листинг 6.9. Комбинирование генераторов type

TtdCombinedPRNG = class (TtdBasePRNG) private

FSeed1 : longint;

FSeed2 : longint;

protected

procedure cpSetSeed1(aValue : longint);

procedure cpSetSeed2(aValue : longint);

public

constructor Create(aSeed1, aSeed2 : longint);

function AsDouble : double; override;

property Seed1 : longint read FSeed1 write cpSetSeed1;

property Seed2 : longint read FSeed2 write cpSetSeed2;

end;

constructor TtdCombinedPRNG.Create(aSeed1, aSeed2 begin

inherited Create;

Seed1 := aSeed1;

Seed2 := aSeed2;

end;

longint);

function TtdCombinedPRNG.AsDouble : double;

const

al = 40014;

m1 = 2147483563;

ql = 53668;

{равно m1 div al}

rl = 12211;

{равно m1 mod al}

a2 = 40692;

m2 = 2147483399;

q2 = 52774;

{равно m2 div a2}

r2 = 3791;

{равно m2 mod a2}

OneOverMl : double = 1.0 / 2147483563.0;

var k : longint;

Z : longint;

begin

{получить случайное число с помощью первого генератора}

k := FSeed1 div ql;

FSeed1 := (al * (FSeed1 - (k * ql))) - (k * rl);

if (FSeed1 <= 0) then

inc(FSeed1, m1);

{получить случайное число с помощью второго генератора}

k := FSeed2 divq2;

FSeed2 := (a2 * (FSeed2 - (k * q2))) - (k * r2);

if (FSeed2 <= 0) then

inc(FSeed2, m2);

{объединить два случайных числа}

Z := FSeed1 - FSeed2;

if (Z <= 0) then

Z := Z + m1 - 1;

Result := Z * OneOverMl;

end;

procedure TtdCombinedPRNG.cpSetSeed1(aValue : longint);

const

m1 = 2147483563;

begin

if (aValue > 0) then

FSeed1 := aValue

else

FSeed1 := GetTimeAsLong;

{убедиться, что случайное число находится в диапазоне от 1 до m-1 включительно}

if (FSeed1 > - m1-1) then

FSeed1 := FSeed1 - (m1-1) + 1;

end;

procedure TtdCombinedPRNG.cpSetSeed2(aValue : longint);

const

m2 = 2147483399;

begin

if (aValue > 0) then

FSeed2 := aValue else

FSeed2 := GetTimeAsLong;

{убедиться, что случайное число находится в диапазоне от 1 до m-1 включительно}

if (FSeed2 >=m2-1) then

FSeed2 := FSeed2 - (m2 - 1) + 1;

end;

Как видите, код метода AsDouble в листинге 6.9 содержит два мультипликативных линейных конгруэнтных генератора: первый с параметрами {а, m} = {40014,2147483563}

и второй с параметрами {а, m} = {40692, 2147483399}.

Циклы обоих генераторов отличаются, но, тем не менее, близки к 2(^31^). Для преобразования промежуточного значения типа longint в значение типа double используется генератор с более длинным циклом.

Приведенный в листинге 6.9 генератор исключает двухмерную регулярность простого мультипликативного линейного конгруэнтного генератора, в чем можно убедиться с помощью программы тестирования. Можно показать, что длина цикла полученного комбинированного генератора составляет примерно 2 * 10(^18^). (Для сравнения, длина цикла стандартного генератора Delphi примерно равна 4 * 10(^9^).) Последовательность, вычисляемая с помощью комбинированного генератора полностью, определяется двумя начальными числами - по одному для каждого внутреннего генератора, в то время как для простого мультипликативного генератора было достаточно одного числа.