6. Комбинаторные задачи

6. Комбинаторные задачи

Я объединил здесь различные головоломки, решение которых для компьютера в принципе нетрудно. Есть конечное число возможных случаев. Мы испытываем их все и выбираем наилучший. К этой категории относится и чемпион мира по шахматам: конечное число шахматных фигур, конечное число правил, конечное число ходов…

Но, конечно, есть препятствие — это число опытов, которые нужно провести. Прежде всего нужно хорошо организоваться, чтобы некоторых попыток и не предпринимать. Нужно выбрать также путь, который предоставляет наиболее возможные шансы дойти до конца, и не вступать на такой путь, который не дает ничего, кроме неудач. В этом — все искусство программирования.

Головоломка 20. Восемь ферзей.

Возьмите на заметку: это самая простая головоломка подобного типа. Поставить на шахматной доске 8 ферзей так, чтобы они друг другу не угрожали. Ферзь может взять все, что находится в этой же строке, что и он, в том же столбце или на той же диагонали. Представим, как обычно, шахматную доску квадратной таблицей полей, среди которых свободные поля помечены точками, а ферзи помечены крестиками (?).

На рис. 28 представлены две попытки решения. На левой доске поставлены 4 ферзя. Все поля строки 6 ими уже блокированы. Продолжать дальше бесполезно. На правой доске мы сумели поставить 7 ферзей, но восьмая строка блокирована.

Я обратил ваше внимание на эту задачу, поскольку ее решения всюду приведены. Ее можно в высшей степени элегантным образом решить с помощью рекурсивной процедуры. Но нетрудно дать решение и в итеративной форме,

Деликатный вопрос связан с представлением шахматной доски. Но и возможности этого выбора также обсуждаются в известных книгах.. Что же тогда остается найти?

Если у вас нет этих книг, то остается найти решение. Нет — решения, поскольку их 92. Но не все они существенно различны, так как шахматная доска обладает симметриями.

Поэтому пытайтесь искать только основные решения, исходя ив которых и используя симметрии шахматной доски, можно найти все остальные решения…

В этом примере вам не следует бояться сложности. Даже самые плохие программы будут все еще достаточно быстры…

?** Головоломка 21. X ферзей.

Поставить на шахматной доске 8 ферзей так, чтобы они друг другу не угрожали, можно. Но трудности, с которыми мы встретились при попытке достичь решения без помощи компьютера, ясно показывают, что нет необходимости в 8 ферзях, чтобы блокировать всю шахматную доску.

Каково наименьшее число ферзей, необходимых для блокирования шахматной доски, так, чтобы не было возможности поставить ни одной фигуры ни на одно поле, чтобы один из уже стоящих ферзей не мог эту фигуру взять?

Так как я вам не задал x, то вам нужно пытаться заставить x либо расти, либо уменьшаться. Впрочем, в этой задаче наши дела идут хуже, чем с 8 ферзями. В предыдущей задаче мы знали, что в каждой строке и каждом столбце обязательно должен быть ферзь. Если ферзей меньше 8, то это уже неверно.

* Головоломка 22. Домино.

Маленькая прелестная головоломна, совсем не трудная. Она была предложена на испытании на проницательность на конкурсе организации АФСЕТ по программированию в 1981 году.

Берутся 7 костяшек из одного набора домино. Напомним, что эти шашки сделаны из двух частей, на каждой из которых либо ничего не написано (чистая сторона), либо очки в числе от 1 до 6,

Задача состоит в том, чтобы образовать из этих 7 костей все возможные цепи, состыковывая костяшки домино частями с равными количествами точек. Нет никакой уверенности, что такая цепь существует.

Не ведите себя так, как некоторые из соревнующихся на этом конкурсе. Я тогда входил в жюри. Мы должны были оценивать работы соревнующихся. Если бы я принимал решения единолично, я потребовал бы, чтобы мне были представлены тексты программ, и я бы судил по самим произведениям. Но другие члены жюри нашли более длинный и более сложный метод, Они приготовили специальные тесты. Они должны были быть испытаны на программах соревнующихся, и нужно было подсчитать число правильных ответов, чтобы расклассифицировать соревнующихся. Новое обсуждение: я выдвигаю оценку, что и один-единственный неверный ответ выражает ошибочность программы и, следовательно, выводит ее из конкурса. В конце концов было решено, что так и будем делать. Все программы, содержащие ошибку, будут рассматриваться как неверные, Если две команды получат одинаково верные ответы, то мы еще раз детально изучим полученные результаты, стараясь разгадать природу ошибки при переходе к данному тесту от уже удавшихся, чтобы отдать одному из них предпочтение. Вот нам и досталось: один ив соревнующихся, думая, что с удавшимися тестами это согласуется, пытался упростить программу для домино. Он сказал себе, что вне всякого сомнения, будут даны кости, из которых никаких цепей ставить нельзя. Его программа читала последовательность костей домино и сообщала НЕВОЗМОЖНО без каких-либо других вычислений. Если бы я не настаивал на своем так решительно, то он был бы не хуже других…

Не поступайте так. Эта задача при всем том нетрудная… Рис. 29 дает пример цепи.

* Головоломка 23. Последовательность 0—1—4—6.

Это головоломка, на которую я натолкнулся, работая над своей диссертацией на ученую степень по физике. Я занимался сетями антенн для радиоастрономии. Сеть антенн состоит из основания, на котором по одной линии размещены отдельные антенны, доставляющие информацию о наблюдаемых нами звездах. Каждая нара антенн дает информацию о некоторой величине, пропорциональной расстоянию между двумя антеннами этой пары. Нас интересуют значения этой величины, образующие арифметическую прогрессию. Таким образом, нужно было располагать антенны таким образом, чтобы расстояния между равными парами образовывали арифметическую прогрессию. Я предложил систему из 4 антенн, расположенных на прямой в точках с абсциссами 0 1 4 6.

Тогда получаемые из них 6 различных пар приводят к расстояниям между антеннами, пропорциональным следующим числам:

0—1 1

4—6 2

1—4 3

0—4 4

1—6 5

0—6 6

Можно сформулировать задачу по-другому. Нужно найти последовательность натуральных чисел a₁, a₂, …, a_n — последовательность, которую можно предполагать возрастающей — такую, чтобы попарные разности членов этой последовательности a_j ? a_i (j > i) были попарно различны и образовывали последовательность всех целых чисел от 1 до n(n ? 1)/2.

Это — еще и проблема трансформатора (см. рис. 30), Если включить во вторичную обмотку 4 выхода так, чтобы число витков между первым и другими выходами находилось в отношениях 1, 4 и 6, то можно получить 6 напряжений на выходе, образующих арифметическую прогрессию.

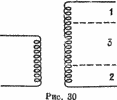
Опустим другие физические задачи, порождающие такие последовательности. Четырехчленная последовательность 0—1—4—6, по-видимому, является наибольшей последовательностью, обладающей свойством порождать последовательность первых целых чисел, не пропуская и не повторяя дважды ни одного из них, при попарном вычитании членов этой последовательности.

Так, для 5 целых можно образовать 10 разностей. Поэтому крайние члены должны быть a₁ = 0, a₅ = 10. Чтобы получить в виде разности 9 из двух членов последовательности, нужно, чтобы либо было a₂ = 1, и тогда a₅ ? a₂ = 9, либо a₄ = 9. Эти два решения легко получаются одно из другого операцией симметрии, Поэтому положим a₂ = 1.

К этому моменту мы получили уже a₁ = 0, a₂ = 1, a₅ = 10. Чтобы получить разность, равную 8, нужно взять

— либо a₃ = 2, но тогда разность, равная 1, получается дважды:

a₃ ? a₂ = a₂ ? a₁

— либо a₄ = 8,

— либо a₄ = 9, но тогда снова дублируется разность 1. Следовательно, a₁ = 0, a₂ = 1, a₄ = 8, a₅ = 10.

Достаточно теперь пересмотреть одно за другим возможные значения а₃ и удостовериться, что каждое ив них дублирует какую-то разность.

Для a₃, равного 2, дублируется разность 1:

3 2

4 4

5 5

6 2

7 1

Таким образом, нет последовательности из 5 целых, попарные разности которых порождают 10 первых натуральных чисел. Допустим теперь возможность повторений в последовательности разностей. Можно ли с помощью 5 членов породить — с помощью их разностей — 9 первых натуральных чисел?

Об этих последовательностях ничего не известно. Пусть дано число n членов последовательности; каково наибольшее число последовательных целых чисел, начиная с 1, которые можно получить с помощью попарных разностей членов последовательности?

Запрограммировать это не очень трудно. Но берегитесь чересчур долгих вычислений!

?** Головоломка 24. Прогулка королевы.

Нет, не в Булонском лесу, если говорить серьезно… Прогулки фигур на шахматной доске — классический сюжет для головоломок. Эйлеровский конь должен обойти всю шахматную доску и вернуться на поле, с которого отправился в путь, не попадая дважды ни на одну клетку. Это настолько общеизвестно, что это уже и не головоломка. Но если вы не знаете решения, я не мешаю вам попробовать.

Случай «королевы» (ферзя) — немного другой. Эта фигура может перемещаться по горизонтали, по вертикали или по диагонали. Назовем «движением» перемещение на некоторое число полей в определенном направлении, Разрешается много раз проходить по одному и тому же полю. Но требуете пройти все поля эа наименьшее возможное число движений, причем, конечно, нужно вернуться на исходное поле. Так как число движений не дано, то не попытаетесь ли вы сначала проделать все вручную, чтобы угнать верхнюю границу…

???* Головоломка 25. Девушки ив пансиона Киркмана.

Пансион Киркмана — это колледж для девушек из высшего общества. Надзирательницей там — мисс Фармер. Каждую среду после полудня она сопровождает класс на прогулку. В своей нарядной униформе, в соломенных шляпках они медленно вышагивают по трое в три ряда. Мисс Фармер несговорчива: «Я не хочу маленьких компаний; вы должны располагаться так, чтобы не оказаться с той же подругой в вашем ряду до тех пор, пока вы не проведете этих прогулок со всеми остальными». На это наши девушки заявили, что поступать так очень трудно. Поэтому мисс Фармер решила сама организовать ряды. Для начала она веяла класс с 9 ученицами. Ей удалось быстро организовать ряды. У каждой ученицы было 8 подружек, и она должна была находиться с двумя новыми подружками каждую неделю, так что мисс Фармер предусмотрела цикл в 4 недели.

Затем мисс Фармер был поручен класс с 15 ученицами. Поэтому было необходимо ввести цикл в 7 недель для того, чтобы каждая ученица была за это время в одном ряду с 14 остальными. Тогда мисс Фармер поняла, в какое ужасное предприятие она оказалась вовлеченной.

Хотите ей помочь? Но заметьте: это вы сами пускаетесь в это ужасное предприятие. Всячески желаю, чтобы вашему микрокомпьютеру было больше нечего делать. Попытайтесь, если все предыдущее не будет отнимать долгие часы…

Эта задача принадлежит Т. П. Киркману и была впервые опубликована в Lady?s and Gentleman?s Diary за 1850 год. Для ее решения нужно пролить немало чернил, и вы можете рассмотреть значения, отличные от 9 и 15. Но выглядит вполне правдоподобным, что 15 — патологическое число, и Роуз Болл [BAL] предложил геометрический подход к решению, если число девочек не равно 15. Может быть, подход с точки зрения информатики позволит вам получить в этой задаче новые результаты…

*** Головоломка 26. Пентамино.

Домино, пентамино: очевидная игра слов, заставляющая перейти от шашек с двумя квадратами, к шашкам с 5 квадрата. Вот двенадцать возможных шашек, получаемых объединением 5 квадратов равной площади.

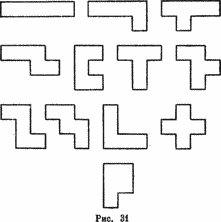
Все они приведены на рис. 31. Эти двенадцать шашек, каждая из которых имеет площадь 5, могут быть собраны в прямоугольник с площадью 60. Есть много решений для прямоугольника 6 ? 10, а также 5 ? 12. Меньше решений для прямоугольника 4 ? 15 и только два для прямоугольника 3 ? 20, если, конечно, не различать решения, отличающиеся только симметрией. Можете ли вы найти их за разумное время на вашем компьютере, проверив, что их действительно именно 2?

Есть много путей подхода к этой задаче, даже если все они действуют согласно одной и той же стратегии: перебрать все возможные попытки. Но есть ходы, которые ни к чему не могут привести. Вы не можете начать с того, чтобы поставить Т в левый нижний угол, как на рис. 32. Ни одна шашка не может замкнуть две заштрихованные области рядом с Т… Здесь есть необходимость и для хорошего представления позиций, но также и немного — для хитрости…

* Головоломка 27. Песенка почти спета.

Знаменитая игра Армана Жаммо уже была упомянута выше (игра 12). Но сейчас мы еще не описываем ее полностью; она довольно трудна для программирования. Вот другая форма, которую проще реализовать и которая еще не лишена интереса. Я верю также, что для любителей математических развлечений здесь есть что делать.

Возьмем случайным образом p двузначных чисел. Возьмем случайным образом также двузначное число s. Соединим эти p чисел между собой сложениями или вычитаниями. Все числа должны быть использованы. Можно ли таким образом получить число s?

При последовательных испытаниях компьютер будет работать быстро. Тогда вы можете попытаться увидеть, что происходит, когда мы заставляем меняться p. Если у вас мало чисел, то у вас и мало шансов получить Если вы берете много чисел (большое p), то, поскольку вы обязаны использовать их все, то у вас снова мало шансов прийти к цели. Мне кажется, что наиболее благоприятны значения p около 8 или 9. Но я не осмеливаюсь гарантировать этого полностью. Нужно быть уверенным в генераторе случайных чисел. Получаете ли вы тот же результат? Я не пытался получить его математическим рассуждением. Может быть, я и неправ. Если я действительно неправ, дайте мне знать об этом!

*** Головоломка 28. Песенка спета.

На этот раз дело идет именно об игре Армана Жаммо. Вам надлежит гадать вашему компьютеру шесть шашек, взятых среди 24; а именно, в набор входят:

по два раза — шашки от 1 до 10,

один раз — шашки 25, 50, 75, 100.

Затем вы задаете искомое число, скажем n, обязательно трехзначное. Требуется соединить значения шашек между собой с помощью четырех операций: сложения, вычитания, умножения и деления — чтобы получить число n. Не обязательно использовать все 6 шашек.

Если число n получить нельзя, то телевизионная игра допускает и числа, близкие к n, и тот, чье число ближе всего к n, и становится победителем.

Теоретически эта программа не должна быть трудной. Есть ограниченное число возможных комбинаций:

— есть 15 способов взять две шашки среди 6 и, самое большее, 4 способа соединить их между собой, следовательно, самое большое 60 комбинаций с двумя шашками. Но их уже гораздо больше для трех шашек. Испытать все комбинации за разумное время не представляется возможным.

Когда вы излагаете решение, вы берете две шашки из 6, соединяете их между собой одной из четырех операций (на самом деле можно считать, что только тремя, начинать с деления — это исключение). Есть 60 (или, скорее, 45) способов это сделать. После этого задача сводится к задаче с 5 шашками. При таком подходе решение кажется более достижимым.

Следовательно, попробуем. Самые большие упрощения возникают, если вы не ищете для данного числа приближенных значений. Компьютер выводит результат, если он его находит; в противном случае он сообщает, что он решения не нашел. Вы сами можете систематически проводить одну попытку за другой. Пусть p_i, p_j, p_k обозначают три из 6 шашек. Вы можете искать решение в виде

p_i * комбинация из 5 оставшихся шашек = n,

p_j + p_i * комбинация из 4 оставшихся шашек = n,

?p_j + p_i * комбинация из 4 оставшихся шашек = n,

±(p_j ? p_k) + p_i * комбинация из 3 оставшихся шашек = n,

где ? означает одну из четырех разрешенных операций. Удивительным образом все это очень быстро и очень часто приводит к точному ответу. Никто на запрещает вам попробовать что-то лучшее…

В соответствии с заглавием примера попытайтесь поэтому для 6 шашек 10, 10, 25, 50, 75, 100 найти 370, 369, 368…