7. Обо всем понемногу

7. Обо всем понемногу

В этом разделе я объединил различные задачи, среди которых далеко не все являются головоломками, по той причине, что опыт показывает: средний программист в них достигает цели не бее труда. Для некоторых из них в различных книгах можно найти многочисленные решения, не всегда правильные, или — во всяком случае — не всегда хорошие, или слишком плохо объясненные. Условия этих задач могут показаться мало привлекательными. Но если в программировании вы любите именно трудности, не поддавайтесь первому впечатлению.

* Головоломка 29. Дихотомический поиск.

Это — совершенно известная задача. Вам предлагается упорядоченная таблица попарно различных элементов; например, в порядке возрастания. Вам предлагается, кроме того, другой элемент: его нужно разместить в таблицу.

Следовало бы уточнить (хоть это и не в моих правилах: обычно я предоставляю вам заботу об уточнении. В этой книге вовсе не я тот человек, который должен аккуратно работать…). Пусть a — таблица с n элементами, упорядоченная так, что

a[i] < a[i + 1] для 1 < i ? n,

и x — элемент, который нужно разместить. Его место

0, если x ? a[1],

i, если a[i] < x ? a[i + 1],

n, если a[n] < x.

Один сотрудник факультета Нотр-Дам де ла Пэ в Намюре изучил 18 программ, опубликованных различными авторами по всему свету и в каждой нашел хоть что-то, за что можно упрекнуть. Всякий раз, когда я получаю новую книгу по программированию (к счастью, я получаю не все), я смотрю, нет ли там случайно исследования этой задачи. Почти во всех случаях это так. Настоящий «ослиный мост»[16] информатики…

* Головоломка 30. Равенство «с точностью до пробелов».

Пусть даны две буквенные цепочки: a и b. Составьте программу, которая может сказать, совпадают ли эти цепочки с точностью до пробелов. Внимание: вы не имеете права изменять цепочки a и b, вы не имеете права порождать новые цепочки. Это запрещает вам удалить пробелы из обеих цепочек или копировать их, удаляя пробелы. Под равенством с точностью до пробелов нужно понимать, что обе цепочки должны быть образованы одними и теми же буквами в одном и том же порядке, если не учитывать пробелы. Такая задача встречается в системах, связанных с практической работой, с программами, потому что пробелы чаще всего рассматриваются в операторах и командах как незначащие.

Если вы находите это совершенно элементарным, вы можете изучить, являются ли данные цепочки обращениями друг друга с точностью до пробелов. Вы можете также увидеть, является ли цепочка палиндромом (т. е. совпадает со своим обращением) с точностью до пробелов, Так, палиндромами являются

А РОЗА УПАЛА НА ЛАПУ АЗОРА

АРГЕНТИНА МАНИТ НЕГРА

Попытайтесь получить правильную (это уж как минимум) и элегантную программу.

Головоломка 31. Анаграмма.

Еще одна головоломка, вопреки ее внешнему виду, Дело в том, чтобы сказать, являются ли две цепочки букв анаграммами друг друга (т. е. получаются ли они друг из друга перестановками букв). Эта задача имеет совершенно различный вид в зависимости от того, разрешите ли вы себе изменять обе цепочки или порождать новые цепочки, или нет. Выбор я предоставляю вам… Может быть, вы заметите, что различные решения следует оценивать в зависимости от соотношения между размерами цепочек и используемого алфавита. Подумайте о крайних случаях: алфавит из 26 букв и цепочка из 1000 символов; алфавит из 1000 символов (это вроде китайского…) и цепочка из 10 символов.

Головоломка 32. Анаграмма с точностью до пробелов.

Та же головоломка, но, кроме того, пробелы не считаются. Вы можете ее еще немного обобщить: являются ли две страницы текста анаграммами одна другой, не считая знаков препинания?

??* Головоломка 33. Переставить две части вектора.

Вам дана таблица a с n элементами. Требуется переставить части с номерами от 1 до m и от m + 1 до n (рис. 33).

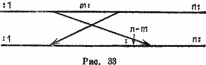
Порядок элементов в каждой ив частой должен быть сохранен[17]. Вы не должны использовать вспомогательную таблицу, Каждый элемент должен быть перемещен не более одного раза.

Это — довольно любопытная задача, которая была предложена мне Давидом Грисом, и которую он исследовал в своей книге [GRI] Это — один из редких случаев, когда я не смог вывести программу из гипотезы рекуррентности, как я это обычно делал [ARS]. В данном случае я сначала придумал программу (ничего особенного, вы ее, конечно, прекрасно составите). И только после того — именно после того — я смог показать, почему эта программа работает правильно.

* Головоломка 34. Задача о равнинах.

Вам дается упорядоченная таблица каких-то элементов, например, телефонный справочник (где фамилии расположены в алфавитном порядке. Здесь мы не учитываем имен). В таблице могут встретиться омонимы (иначе говоря, последовательности из совпадающих элементов), как в телефонном справочнике. Требуется найти наиболее длинные омонимы: больше ли МАРТЫНОВых, чем СЕМЕНОВых?

Я использовал для этой головоломки название, данное ей в книге Давида Гриса [GRI]. Если вместо того, чтобы веять для иллюстрации таблицу фамилий, вы берете

таблицу чисел, расположенных в неубывающем порядке, то такая таблица составлена иэ участков возрастания, подъемов и ровных участков, «равнин». Тогда нужно найти наиболее длинную равнину.

Эта задача оказывается не вполне одной и той же в зависимости от того, ищете ли вы только наибольшую длину равнины (что делает Д. Грис) или ищете одновременно и длину ряда омонимов и сам наиболее часто встречающийся омоним (что предлагаю вам я).

G этой задачей связана неприятная для меня история. Я намеревался продумать эту задачу в Нанси также, впрочем, как и Давид Грис. Я довольно легко обнаружил два решения, различные по духу, но не по виду, что поставило передо мной задачи преобразования программ (каким образом различные отправные точки могут привести, с точностью до нескольких манипуляций, к одной и той же программе). Как и рассказывает в своей книге Давид Грис, я очень гордился своими решениями, пока не обнаружил в той же книге Д. Гриса решение, принадлежащее Майклу Гриффиту: его решение намного проще…

Сумеете ли вы найти простое решение?

??** Головоломка 35. Самая длинная возрастающая подпоследовательность.

Пусть дана таблица a из n каких-либо чисел (но если это может доставить вам удовольствие — из натуральных чисел. Это неважно). Подпоследовательность этой таблицы есть последовательность чисел, выделенная в порядке возрастания номеров. Более точно, последовательность

a[i₁] a[i₂] a[i₃] … a[i_p]

есть подпоследовательность последовательности а, если i₁ < i₂ < … < i_p. (Числа идут в одном и том же порядке в таблице a и в ее подпоследовательности, но эта формулировка двусмысленна.)

Последовательность возрастает[18], если, кроме того,

a[i₁] ? a[i₂] ? a[i₃] ? … ? a[i_p].

Требуется выделить из a самую длинную возрастающую подпоследовательность. Вы имеете право использовать вспомогательные векторы.

Можно найти исследование этой задачи в нескольких книгах и на нее изведено немало чернил (да и мела тоже: я видел ее исследования в трудах международных семинаров). Кроме того, совершенно не одно и то же — довольствуемся ли мы определением максимальной длины и даже последнего члена самой длинной возрастающей подпоследовательности последовательности a (внимание: может случиться, что есть много таких подпоследовательностей одинаковой длины) или же мы хотим получить также список членов такой максимальной последовательности.

Иногда в условие вводят дополнительное ограничение: число требуемых операций должно быть порядка n * In(n). Я не уверен, что это действительное ограничение. Если вы найдете решение, то оно, скорее всего, будет обладать этим свойством.

??** Головоломка 36. Самое длинное слово.

Заглавие вводит в заблуждение… Однажды мы проводили экзамен у наших учеников в DEUG по составлению программы, которая сообщает, скрыто ли данное слово в данной фразе, иначе говоря, встречаются ли буквы данного слова в том же порядке в данной фразе. Так, в следующей фразе (взятой из «Ярмарки у скупцов» Жана Шарля):

«Je peux te donner l?adresse d?un excellent cireur de parquets: il se rend ? domicile»

слово TONDEUSE скрыто (соответствующие буквы подчеркнуты), но ни слово GAZON (нет буквы G), ни слово DOMINATEUR (все буквы есть, но в неправильном порядке) не содержатся.

Но это не головоломка, это совсем просто (уж это точно…). Я спрашиваю вас о другом — найти, какое слово наибольшей длины скрыто одновременно в двух фразах. На самом деле, конечно, речь идет не о слове, а скорее о последовательности букв: какая наиболее длинная последовательность букв может быть обнаружена в одном и том же порядке в двух фразах. Если это может вам помочь, то вот другой пример из «Ярмарки у скупцов»:

«А l?occasion du 14 juillet, les hommes remplaceront les cruches dans les chambres».

Моя Программа сообщает мне, что наиболее длинная последовательность букв, которая встречается одновременно в одном и том же порядке в обоих отрывках, это набор

JETEOERLARNLECREDASLSAME

Вы можете проверить, что эти буквы действительно встречаются в обеих фразах (во второй из них они подчеркнуты). Но вручную невозможно проверить, что этот набор — самый длинный из возможных. Если вы не можете доверять вашей программе, не пишите ее…

Если вы сожалеете, что я злоупотребил названием, которое напоминает совсем о другом, а именно, об игре Армана Жаммо: найти наиболее длинное слово, которое можно образовать из 9 данных букв, то я не запрещаю вам исследовать также и эту игру. Но тут я вижу два препятствия. Во-первых, с точки зрения процесса ее создания есть очень мало того, что требуется обнаружить или открыть (если не пришлось открывать какой-нибудь словарь Скраббля). Далее, нужно ввести в компьютер настоящий словарь, что предполагает большой объем хранения и чудовищный труд отстукивания по клавишам, совершенно лишенный интереса…

?*** Головоломка 37. Белый прямоугольник.

Ах, ах! Тут-то я вас и поймал. Вы немедленно вообразили себе какую-нибудь не поддающуюся пересказу историю… Такое в книгах по информатике бывает редко, но бывает [SIK]. В своем сочинении о языке ЛИСП Лоран Сиклосси должен был использовать многочисленные примеры буквенных цепочек, и все составленные им цепочки одна смешнее другой. Это и вдохновило меня на предыдущую головоломку. Я предложил своему издателю перевести сочинение Сиклосси, что не должно было быть таким уж трудным, поскольку автор использует французские фразы, чтобы блеснуть учтивостью (иначе он бы говорил это по-латыни). Но Сиклосси, который превосходно владеет французским языком — несмотря на то, что он профессор информатики в Соединенных Штатах, — захотел изменить примеры к французской версии книги, используя «акрофонические перестановки» — перестановки букв или слогов, создающие слова с новым значением… Издатель не согласился, и французская литература потеряла прекрасное сочинение о языке ЛИСП… Если вы читаете по-английски и если вы хотите выучить ЛИСП, почему вам нельзя развлекаться, учась?

Здесь речь идет совсем о другом. Эта задача была предложена как одна из четырех тем на конкурсе программирования в АФСЕТ несколько лет назад. Вам дана прямоугольная решетка для кроссворда. Найдите белый (т. е. не содержащий вычеркнутых черных клеток) прямоугольник наибольшей площади, вписанный в решетку (квадрат есть частный случай прямоугольника).

На рис. 34 есть прямоугольник площади 8 в левом нижнем углу и есть квадрат площади 9. Это — хороший ответ. Программа, которую вы должны составить, должна читать размеры сетки (число строк и столбцов), затем— координаты черных полей и, наконец, давать прямоугольник наибольшей площади, например, указанием координат двух противоположных вершин.

Для программистов на конкурсе АФСЕТ это не было легкой задачей. Она оказалась едва ли не наиболее трудной задачей, будучи единственной задачей, доставившей мне затруднения (см. головоломку 22, другое упражнение на том же конкурсе). Один из соревнующихся достиг цели, решительно пренебрегая эффективностью. Вы-то не очень ограничены временем (по крайней мере временем размышления или временем программирования). Попытайтесь составить программу, время вычисления которой не слишком быстро растет вместе с размером сетки.

Головоломка 38. Математическая композиция.

Ж.-К. Байиф [BAI], французский язык которого очень отточен, представил эту головоломку под названием «арифметическая композиция» в своей книге, из которой в ее и заимствую, Композиция состоит из четырех вопросов, связанных с вычислением площади. Один из вопросов относится к полной поверхности куба, сторона которого измеряется целым числом метров, Вот ответы учеников на различные вопросы:

(Это — величины площадей в квадратных метрах, предложенные учениками.) Преподаватель ставит 5 за верный ответ и 0 за неверный ответ. Один-единственный из учеников получил 0. Кто оказался первым? Вне всякого сомнения, вы можете сказать больше. Эта головоломка кажется мне особенно подходящей для ее решения на компьютере…

?? Головоломка 39. Другая головоломка Давида Гриса.

Пусть дан вектор, образованный n целыми числами. Подпоследовательностью этого вектора называется набор элементов, в котором индексы идут подряд. Найти подпоследовательность с максимальной суммой. Если вы предпочитаете другую формулировку, то найдите индексы i, j, для которых величина

a_i + a_i+1 + … + a_j?1 + a_j

максимальна. Внимание: время вычисления не должно расти намного быстрее, чем n, когда n увеличивается…

Эта головоломка до некоторой степени напоминает головоломку о возрастающих подпоследовательностях, но она гораздо менее сложна. Подумайте: линейная зависимость от n! Да ведь это, грубо говоря, означает, что каждый элемент вектора рассматривается только один раз. Вам следует составить цикл

ДЛЯ i := 1 ШАГ 1 ДО n ВЫПОЛНЯТЬ … ВЕРНУТЬСЯ

И никаких циклов в этом цикле! В ответе вы получаете искомые индексы. Озадачивающе, не так ли? Я потерял на это немало времени. И тем не менее, какое простое решение!

Как вы находите?