14.4.1. Введение в двоичные деревья

14.4.1. Введение в двоичные деревья

Массивы являются почти простейшим видом структурированных данных. Их просто понимать и использовать. Хотя у них есть недостаток, заключающийся в том, что их размер фиксируется во время компиляции. Таким образом, если у вас больше данных, чем помещается в массив, вам не повезло. Если у вас значительно меньше данных, чем размер массива, память расходуется зря. (Хотя на современных системах много памяти, подумайте об ограничениях программистов, пишущих программы для внедренных систем, таких, как микроволновые печи и мобильные телефоны. С другого конца спектра, подумайте о проблемах программистов, имеющих дело с огромными объемами ввода, таких, как прогнозирование погоды.

В области компьютерных наук были придуманы многочисленные динамические структуры данных, структуры, которые увеличивают и уменьшают свой размер по требованию и которые являются более гибкими, чем простые массивы, даже массивы, создаваемые и изменяемые динамически с помощью malloc() и realloc(). Массивы при добавлении или удалении новых элементов требуется также повторно сортировать.

Одной из таких структур является дерево двоичного поиска, которое мы для краткости будем называть просто «двоичным деревом» («binary tree»). Двоичное дерево хранит элементы в сортированном порядке, вводя их в дерево в нужном месте при их появлении. Поиск по двоичному дереву также осуществляется быстро, время поиска примерно такое же, как при двоичном поиске в массиве. В отличие от массивов, двоичные деревья не нужно каждый раз повторно сортировать с самого начала при добавлении к ним элементов.

У двоичных деревьев есть один недостаток. В случае, когда вводимые данные уже отсортированы, время поиска в двоичном дереве сводится ко времени линейного поиска. Техническая сторона этого вопроса должна иметь дело с тем, как двоичные деревья управляются внутренне, что вскоре будет описано.

Теперь не избежать некоторой формальной терминологии, относящейся к структурам данных. На рис. 14.1 показано двоичное дерево. В информатике деревья изображаются, начиная сверху и расширяясь вниз. Чем ниже спускаетесь вы по дереву, тем больше его глубина. Каждый объект внутри дерева обозначается как вершина (node). На вершине дерева находится корень дерева с глубиной 0. Внизу находятся концевые вершины различной глубины. Концевые вершины отличают по тому, что у них нет ответвляющихся поддеревьев (subtrees), тогда как у внутренних вершин есть по крайней мере одно поддерево. Вершины с поддеревьями иногда называют родительскими (parent), они содержат порожденные вершины (children).

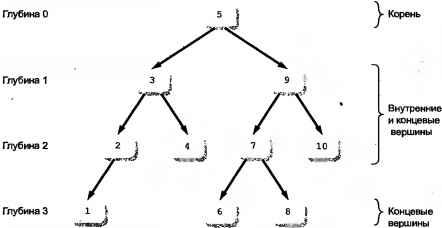
Рис. 14.1. Двоичное дерево

Чистые двоичные деревья отличаются тем, что каждая вершина содержит не более двух порожденных вершин. (Деревья с более чем двумя вершинами полезны, но не существенны для нашего обсуждения.) Порожденные вершины называются в этом случае левой и правой соответственно.

Деревья двоичного поиска отличаются еще и тем, что значения, хранящиеся в левой порожденной вершине, всегда меньше значения в родительской вершине, а значения, хранящиеся в правой порожденной вершине, всегда больше значения в родительской вершине. Это предполагает, что внутри дерева нет повторяющихся значений. Этот факт также объясняет, почему деревья не эффективны при работе с предварительно отсортированными данными: в зависимости от порядка сортировки, каждый новый элемент данных сохраняется либо только слева, либо только справа от находящегося впереди него элемента, образуя простой линейный список.

К двоичным деревьям применяют следующие операции:

Ввод

Добавление к дереву нового элемента.

Поиск

Нахождение элемента в дереве.

Удаление

Удаление элемента из дерева.

Прохождение (traversal)

Осуществление какой-либо операции с каждым хранящимся в дереве элементом. Прохождение дерева называют также обходом дерева (tree walk). Есть разнообразные способы «посещения» хранящихся в дереве элементов. Обсуждаемые здесь функции реализуют лишь один из таких способов. Мы дополнительно расскажем об этом позже.