В поисках прямоугольного треугольника

Давайте закончим главу задачей, в решении которой пригодятся и генераторы списков, и кортежи. Предположим, что требуется найти прямоугольный треугольник, удовлетворяющий всем следующим условиям:

• длины сторон являются целыми числами;

• длина каждой стороны меньше либо равна 10;

• периметр треугольника (то есть сумма длин сторон) равен 24.

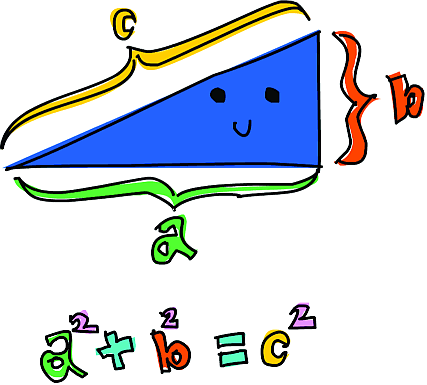
Треугольник называется прямоугольным, если один из его углов является прямым (равен 90 градусам). Прямоугольные треугольники обладают полезным свойством: если возвести в квадрат длины сторон, образующих прямой угол, то сумма этих квадратов окажется равной квадрату стороны, противоположной прямому углу. На рисунке стороны, образующие прямой угол, помечены буквами a и b; сторона, противоположная прямому углу, помечена буквой c. Эта сторона называется гипотенузой.

Первым делом построим все тройки, элементы которых меньше либо равны 10:

ghci> let triples = [(a,b,c) | c <– [1..10], b <– [1..10], a <– [1..10]]

Мы просто собираем вместе три списка, и наша производящая функция объединяет их в тройки. Если вы вызовете функцию triples в GHCi, то получите список из тысячи троек. Теперь добавим условие, позволяющее отфильтровать только те тройки, которые соответствуют длинам сторон прямоугольных треугольников. Мы также модифицируем эту функцию, приняв во внимание, что сторона b не больше гипотенузы, и сторона a не больше стороны b.

ghci> let rightTriangles = [ (a,b,c) | c <– [1..10], b <– [1..c], a <– [1..b], a 2 + b 2 == c 2]

ПРИМЕЧАНИЕ. В консоли интерпретатора GHCi невозможно определять программные сущности в нескольких строках. Но в данной книге нам иногда приходится разбивать определения на несколько строк, чтобы код помещался на странице. В противном случае книга оказалась бы такой широкоформатной, что для неё вам пришлось бы купить гигантский книжный шкаф!

Почти закончили. Теперь давайте модифицируем функцию, чтобы получить треугольники, периметр которых равен 24.

ghci> let rightTriangles' = [ (a,b,c) | c <– [1..10], b <– [1..c], a <– [1..b], a 2 + b 2 == c 2, a+b+c == 24]

ghci> rightTriangles'

[(6,8,10)]

Вот и ответ! Это общий шаблон в функциональном программировании. Вы берёте начальный набор решений и затем применяете преобразования и фильтруете их, пока не получите результат.