9.3. Эволюция

9.3. Эволюция

Проектирование интерфейса классов

После того, как выработаны основные принципы построения архитектуры системы, остающаяся работа проста, но зачастую довольно скучна и утомительна. Следующий этап будет состоять в реализации трех или четырех семейств классов (таких, как очередь, множество и дерево) в соответствии с выбранной архитектурой, и в последующем их тестировании в нескольких приложениях [Вирфс-Брок считает, что необходимо тестировать среду разработки по крайней мере на трех приложениях, чтобы проверить правильность стратегических и тактических решений [15]].

Наиболее тяжелой частью данного этапа является создание подходящего интерфейса для каждого базового класса. И здесь, в процессе изолированной разработки отдельных классов (см. главу 6), нельзя забывать о задаче обеспечения глобального соответствия всех частей системы друг другу. В частности, для класса Set можно определить следующий протокол:  

? setHashFunction   Устанавливает функцию хеширования для элементов множества. 

 ? clear   Очищает множество. 

 ? add   Добавляет элемент к множеству. 

 ? remove   Удаляет элемент из множества. 

 ? setUnion   Объединяет с другим множеством. 

 ? intersection   Находит пересечение с другим множеством. 

 ? difference   Удаляет элементы, которые содержатся в другом множестве. 

 ? extent   Возвращает количество элементов в множестве. 

 ? isEmpty   Возвращает 1, если множество пусто. 

 ? isMember   Возвращает 1, если данный элемент принадлежит множеству. 

 ? isSubset   Возвращает 1, если множество является подмножеством другого множества. 

 ? isProperSubset   Возвращает 1, если множество является собственным подмножеством другого множества. 

  Подобным же образом можно определить протокол класса BinaryTree:  

? clear   Уничтожает дерево и всех его потомков. 

 ? insert   Добавляет новый узел в корень дерева. 

 ? append   Добавляет к дереву потомка. 

 ? remove   Удаляет потомка из дерева. 

 ? share   Структурно делит данное дерево. 

 ? swapChild   Переставляет потомка с деревом. 

 ? child   Возвращает данного потомка. 

 ? leftChild   Возвращает левого потомка. 

 ? rightChild   Возвращает правого потомка. 

 ? parent   Возвращает родителя дерева. 

 ? setItem   Устанавливает элемент, ассоциированный с деревом. 

 ? hasChildren   Возвращает 1, если у дерева есть потомки. 

 ? isNull   Возвращает 1, если дерево нулевое. 

 ? isShared   Возвращает 1, если дерево структурно разделено. 

 ? isRoot   Возвращает 1, если дерево имеет корень. 

 ? itemAt   Возвращает элемент, ассоциированный с деревом. 

  Для схожих операций мы используем схожие имена. При разработке интерфейса мы также проверяем полученное решение на соответствие критериям достаточности, полноты и примитивности (см. главу 3).

Классы поддержки

При реализации класса, ответственного за манипуляции с текстовыми строками, мы столкнулись с тем, что возможностей, предоставляемых классами поддержки Bounded и Unbounded, явно недостаточно. Ограниченная форма, в частности, оказывается неэффективной для работы со строками с точки зрения памяти, так как мы должны инстанцировать эту форму в расчете на максимально возможную строку, и следовательно понапрасну расходовать память на более коротких строках. Неограниченная форма, в свою очередь, неэффективна с точки зрения быстродействия: поиск элемента в строке может потребовать последовательного перебора всех элементов связного списка. По этим причинам нам пришлось разработать третий, "динамический" вариант:  

? Динамический   Структура хранится в "куче" в виде массива, длина которого может уменьшаться или увеличиваться. 

  Структура хранится в "куче" в виде массива, длина которого может уменьшаться или увеличиваться.

Соответствующий класс поддержки Dynamic представляет собой промежуточный вариант по отношению к ограниченному и неограниченному классам, обеспечивающий быстродействие ограниченной формы (возможно прямое индексирование элементов) и эффективность хранения данных, присущую неограниченной форме (память выделяется только под реально существующие элементы).

Ввиду того, что протокол данного класса идентичен протоколу классов Bounded и Unbounded, добавление к библиотеке нового механизма не составит большого труда. Мы должны создать по три новых класса для каждого семейства (например, DynamicString, GuardedDynamicString и SynchronizedDynamicString). Таким образом, мы вводим следующий класс поддержки:

template<class Item, class StorageManager> class Dynamic { public:

Dynamic(unsigned int chunkSize);

protected:

Item* rep; unsigned int size; unsigned int totalChunks; unsigned int chunkSize; unsigned int start; unsigned int stop; void resize(unsigned int currentLength, unsigned int newLength, int preserve - 1); unsigned int expandLeft(unsigned int from); unsigned int expandRight(unsigned int from); void shrinkLeft(unsigned int from); void shrinkRight(unsigned int from);

};

Последовательности разбиваются на блоки в соответствии с аргументом конструктора chunkSize. Таким образом, клиент может регулировать размер будущего объекта.

Из интерфейса видно, что класс Dynamic имеет много общего с классами Bounded и Unbounded. Отличия в реализации трех типов классов каждого семейства будут минимальны.

Займемся теперь классом ассоциативных массивов. Его реализация потребует новой переработки ограниченной, динамической и неограниченной форм. В частности, поиск элемента в ассоциативном массиве требует слишком много времени, если его приходится вести перебором всех элементов. Но производительность можно значительно увеличить, используя открытые хеш-таблицы.

Абстракция открытой хеш-таблицы проста. Таблица представляет собой массив последовательностей, которые называются клетками. Помещая в таблицу новый элемент, мы сначала генерируем хеш-код по этому элементу, а затем используем код для выбора клетки, куда будет помещен элемент. Таким образом, открытая хеш-таблица делит длинную последовательность на несколько более коротких, что значительно ускоряет поиск.

Соответствующую абстракцию можно определить следующим образом:

template<class Item, class Value, unsigned int Buckets, class Container> class Table { public:

Table(unsigned int (*hash)(const Item&)); void setHashFunction(unsigned int (*hash)(const Item&)); void clear(); int bind(const Item&, const Value&); int rebind(const Item&, const Value&); int unbind(const Item&); Container* bucket(unsigned int bucket); unsigned int extent() const; int isBound(const Item&) const; const Value* valueOf(const Item&) const; const Container *const bucket(unsigned int bucket) const;

protected:

Container rep[Buckets];

};

Использование класса Container в качестве аргумента шаблона позволяет применить абстракцию хеш-таблицы вне зависимости от типа конкретной последовательности. Рассмотрим в качестве примера (сильно упрощенное) объявление неограниченного ассоциативного массива, построенного на базе классов Table и Unbounded:

template<class Item, class Value, unsigned int Buckets, class StorageManager> class UnboundedMap : public Map<Item, Value> { public:

UnboundedMap(); virtual int bind(const Item&, const Value&); virtual int rebind(const Item&, const Value&); virtual int unbind(const Item&);

protected:

Table<Item, Value, Buckets, Unbounded<Pair<Item, Value>, StorageManager>> rep;

};

В данном случае мы истанцируем класс Table контейнером unbounded. Рис. 9-12 иллюстрирует схему взаимодействия этих классов.

В качестве свидетельства общей применимости этой абстракции мы можем использовать класс Table при реализации классов множеств и наборов.  

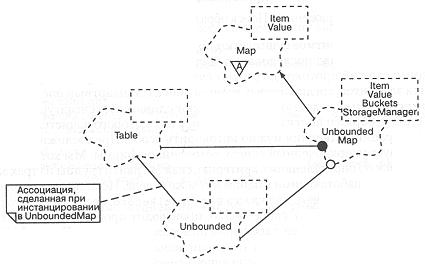
Рис. 9-12. Классы поддержки.

Инструменты

Для нашей библиотеки основная роль шаблонов заключается в параметризации структур типами элементов, которые будут в них содержаться; поэтому такие структуры называют классами-контейнерами. Но, как видно из определения класса Table, шаблоны можно использовать также для передачи классу некоторой информации о реализации.

Еще более сложная ситуация возникает при создании инструментов, которые оперируют с другими структурами. Как уже отмечалось, алгоритмы тоже можно представить в виде классов, объекты которых будут выступать в роли агентов, ответственных за выполнение алгоритма. Такой подход соответствует идее Джекобсона об объекте управления, который служит связующим звеном, осуществляющим взаимодействие обычных объектов [16]. Преимущество данного подхода состоит в возможности создания семейств алгоритмов, объединенных наследованием. Это не только упрощает их использование, но также позволяет объединить концептуально схожие алгоритмы.

Рассмотрим в качестве примера алгоритмы поиска образца внутри последовательности. Существует целый ряд подобных алгоритмов:  

? Простой   Поиск образца последовательной проверкой всей структуры. В худшем случае временной показатель сложности данного алгоритма будет O(pn), где p - длина образца и n - длина последовательности. 

 ? Кнут-Моррис-Пратт   Поиск образца с временным показателем O(p+n) (Knuth-Morris-Pratt). Алгоритм не требует создания копий, поэтому годится для поиска в потоках. 

 ? Бойер-Мур   Поиск с сублинейным временным показателем (Boyere-Moore) O(c(p+n)), где c меньше 1 и обратно пропорционально p. 

 ? Регулярное выражение   Поиск образца, заданного регулярным выражением. 

  У всех этих алгоритмов существуют по крайней мере три общие черты: все они проводят операции над последовательностями (и значит работают с объектами, имеющими схожий протокол), требуют существования операции сравнения для того типа элементов, среди которых ведется поиск (стандартный оператор сравнения может оказаться недостаточным), и имеют одинаковую сигнатуру вызова (целевую строку, образец поиска и индекс элемента, с которого начнется поиск).

Об операции сравнения нужно поговорить особо. Предположим, например, что существует упорядоченный список сотрудников фирмы. Мы хотим произвести в нем поиск по определенному критерию, скажем, найти группы из трех записей с сотрудниками, работающими в одном и том же отделе. Использование оператора operator==, определенного для класса PersonnelRecord, не даст нужного результата, так как этот оператор, скорее всего, производит проверку в соответствии с другим критерием, например, табельным номером сотрудника. Поэтому нам придется специально разработать для этой цели новый оператор сравнения, который запрашивал бы (вызовом соответствующего селектора) название отдела, в котором работает сотрудник. Поскольку каждый агент, выполняющий поиск по образцу, требует своей функции проверки на равенство, мы можем разработать общий протокол введения такой функции в качестве части некоторого абстрактного базового класса. Рассмотрим в качестве примера следующее объявление:

template<class Item, class Sequence> class PatternMatch { public:

PatternMatch(); PatternMatch(int (*isEqual)(const Item& x, const Item& y)); virtual ~PatternMatch(); virtual void setIsEqualFunction(int (*)(const Item& x, const Item& y)); virtual int match(const Sequence& target, const Sequences; pattern, unsigned int start = 0) = 0; virtual int match(const Sequence&; target, unsigned int start = 0) = 0;

protected:

Sequence rep; int (*isEqual)(const Item& x, const Item& y);

private:

void operator=(coust PattemMatcb&) {} void operator==(const PatternMatch&) {} void operator!=(const PatternMatch&) {}

};

Операции присваивания и сравнения на равенство для объектов данного класса и его подклассов невозможны, поскольку мы использовали соответствующие идиомы. Мы сделали это, потому что операции присваивания и сравнения не имеют смысла для абстракций агентов.

Теперь опишем конкретный подкласс, определяющий алгоритм Бойера-Мура:

template<class Item, class Sequence> class BMPatternMatch : public PatternMatch<Item, Sequence> { public:

BMPatternMatch(); BMPattemMatch(int (*isEqual) (const Item& x, const Item& y)); virtual ~BMPattemMatch(); virtual int match(const Sequence& target, const Seque unsigned int start = 0); virtual int match(const Sequence& target, unsigned in

protected:

unsigned int length; unsigned int* skipTable; void preprogress(const Sequence& pattern); unsigned int itemsSkip(const Sequence& pattern, const Item& item);

};  

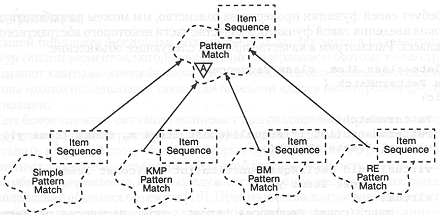
Рис. 9-13. Классы поиска.

Открытый протокол этого класса полностью копирует соответствующий протокол своего суперкласса. Кроме того, его описание дополнительно включает два элемента данных и две вспомогательные функции. Одна из особенностей данного класса состоит в создании временной таблицы, которая используется для пропуска длинных неподходящих последовательностей. Эти добавочные элементы нужны для реализации алгоритма.

На рис. 9-13 приведена иерархия классов поиска. Иерархия подобного типа применима для большинства инструментов библиотеки. При этом формируются сходные по структуре семейства классов, что позволяет пользователям легко в них ориентироваться и выбирать те, которые наилучшим образом подходят для их приложений.