Выбор вершин со множеством рёбер

Выбор вершин со множеством рёбер

В идеале меш должен содержать грани, которые состоят из только четырех вершин (эти грани обычно именуются  quads — четырёхугольники), и у них должны быть относительно одинаковые размеры. Такая конфигурация оптимальна при деформации меша, что часто бывает необходимо в анимации. Конечно, нет ничего действительно ужасного в трехсторонних гранях (tris), но в общих чертах  лучше избегать их, поскольку небольшие треугольные грани всё портят при применении модификатора subsurface, заставляя его показывать неприглядную рябь.

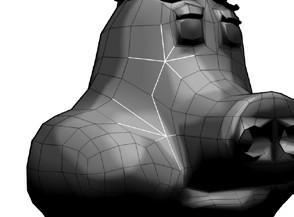
Но даже когда у вас есть меш, состоящий только из четырёхугольников, некоторые вершины являются центром более, чем четырех рёбер. Эти вершины иногда называют полюсами, отсюда и название скриптов в следующих разделах. Если количество рёбер чрезмерное, скажем шесть или больше (как показано в предыдущем скриншоте), такой участок может стать трудным для деформации, и трудным для манипуляций разработчиком модели. В большом и сложном меше эти вершины может быть сложно находить и, следовательно, нам нужно средство выбора таких вершин.

Выбор полюсов

Для того чтобы выбрать вершины с определённого числа шагов, мы можем выполнить следующие шаги:

1. Независимо проверить, что активный объект - это меш.

2. Независимо убедиться, что мы - в режиме объектов.

3. Показать всплывающее меню для ввода минимального количества рёбер.

4. Для каждой вершины:

• Итерация по всем рёбрам, подсчет вхождений вершины

• Если счет - больше или равен минимуму, выбрать вершину

Этот метод - прямой и простой. Функция, которая ответственна за фактическую работу, показана ниже (полный скрипт называется poleselect1.py). Она близко следует нашей схеме. Фактический выбор вершин осуществляется путем присвоения атрибуту вершины sel. Заметим также, что атрибуты v1 и v2 объекта ребра не являются индексами в атрибуте verts нашего меша, а ссылаются на объекты MVert. Вот почему нам нужно извлекать атрибуты index для сравнения.

def poleselect1(me,n=5):

   for v in me.verts:

      n_edges=0

      for e in me.edges:

         if e.v1.index == v.index or

                    e.v2.index == v.index:

            n_edges+=1

            if n_edges >= n:

               v.sel = 1

               break

Выбор полюсов, ещё раз

Вы вероятно обратили внимание, что мы повторяли обход списка рёбер по новой для каждой вершины (выделено в предыдущем коде). Это может быть дорого с точки зрения производительности и эта стоимость даже усложнена необходимостью сравнивать индексы, которые нужно извлекать снова и снова. Возможно ли написать более эффективный код, который, тем не менее, останется удобочитаемым? Да, если мы будем следовать этой стратегии:

1. Независимо проверить, что активный объект - это меш.

2. Независимо убедиться, что мы - в режиме объектов.

3. Показать всплывающее меню для ввода минимального количества рёбер.

4. Инициализировать словарь, проиндексированный индексом вершин, который будет содержать счетчики рёбер.

5. Повторять цикл по всем рёбрам (обновлять счет для обеих вершин, на которые ссылается ребро).

6. Повторять цикл по всем элементам словаря (если счет - больше или равен минимуму, выбираем вершину).

Используя эту стратегию, мы просто выполняем две, возможно длительных, итерации ценой памяти, требуемой на хранение словаря (ничто не бесплатно). Увеличение скорости незначительно для небольших мешей, но может быть серьёзным (Я отмечал 1,000-кратное повышение скорости у небольшого меша в 3,000 вершин) для больших мешей, и они - именно тот тип мешей, где кому-нибудь может понадобиться средство, подобное этому.

Наша переделанная функция выбора показана ниже (полный скрипт называется poleselect.py). Сначала отметьте оператор import. Словарь, который мы будем использовать, называется словарь со значением по-умолчанию (default dictionary) и предоставляется модулем Питона collections. словарь по-умолчанию является словарем, который инициализирует отсутствующие элементы при первой ссылке на них. Так как мы хотим увеличивать на 1 значение счетчика каждой вершины, на которую ссылается ребро, мы должны были бы или инициализировать наш словарь нулевыми величинами для каждой вершины в меше заблаговременно, или проверять каждый раз, проиндексирована ли уже вершина, для которой мы хотим увеличить счет, и если нет, инициализировать его. Словарь по умолчанию позволяет забыть о необходимости инициализировать все заранее, и является очень удобочитаемой идиомой.

Мы создаем наш словарь, вызывая функцию defaultdictionary() (функция, возвращающая новый объект, поведение которого настраивается некоторым аргументом, передаваемым в функцию, называется фабрикой в объектно-ориентированных кругах) с аргументом int. Аргумент должен быть функцией, не принимающей никаких аргументов. Встроенная функция int(), которую мы здесь используем, возвращает целую величину, равную нулю, когда вызывается без аргументов. Каждый раз, когда мы обращаемся к нашему словарю по несуществующему ключу, создаётся новый элемент, и его значением будет результат, возвращённый нашей функцией int(), то есть нуль. Существенные строки - те две, где мы увеличиваем счетчик рёбер (выделенная часть следующего кода). Мы могли бы написать это выражение немного другим способом, для иллюстрации, почему нам нужен словарь со значением по-умолчанию:

edgecount[edge.v1.index] = edgecount[edge.v1.index] + 1

Элемент словаря, на который мы ссылаемся с правой стороны выражения, не будет еще существовать всякий раз, когда мы ссылаемся на индекс вершины, с которой мы сталкиваемся впервые. Конечно, мы могли бы проверить это заранее, но это сделало бы код в целом гораздо менее читабельным.

from collections import defaultdict

def poleselect(me,n=5):

   n_edges = defaultdict(int)

   for e in me.edges:

      n_edges[e.v1.index]+=1

      n_edges[e.v2.index]+=1

   for v in (v for v,c in n_edges.items() if c>=n ):

      me.verts[v].sel=1