Преобразование топологии меша
Преобразование топологии меша
Создание существа из строительных блоков требует, чтобы мы применяли дублирование, масштабирование, и отражение к этим строительным блокам прежде, чем мы склеим их вместе. В Блендере 2.49, это означает, что мы должны определить некоторые вспомогательные функции (утилиты), чтобы выполнить эти действия, так как они не присутствуют в API. Мы определяем эти вспомогательные функции в модуле Tools (инструменты), но мы осветим некоторые из них здесь, так как они покажут несколько интересных методов.
Некоторые действия, как например, масштабирование вокруг средней точки или перемещение вершин просты, но присоединение группы вершин к другой сложнее, так как мы хотели бы предотвратить скрещивание рёбер друг с другом и сохранить грани плоскими и недеформированными. Мы не можем просто соединить два набора вершин (или краевых цикла) вместе. Но пробуя различные отправные точки в рёберном цикле, и проверяя, если такой выбор минимизирует расстояние между всеми парами вершин, мы обеспечиваем, чтобы не было никаких рёберных пересечений, и искажения были минимальными (хотя мы не можем полностью предотвратить искажения граней, если рёберные циклы очень разнородные по форме).
Схема кода сшивания рёберных циклов
В функции, которая создает новые грани, мы должны выполнить следующие шаги:
1. Удостовериться, что оба рёберных цикла цикла имеют одинаковую и ненулевую длину.
2. Для каждого ребра в цикле 1:
1. Найти ребро в цикле 2, которое ближе всего.
2. Создать грань, соединяющую эти два ребра.
Функция, которая осуществляет эту довольно сложную на вид схему:
def bridge_edgeloops(e1,e2,verts):
e1 = e1[:]
e2 = e2[:]
faces=[]
if len(e1) == len(e2) and len(e1) > 0 :
Функция принимает аргументы: два списка рёбер и список вершин. Рёбра представлены в виде кортежей двух целых (индексы в списке вершин verts), а вершины - в виде кортежей координат x, y, и z.
Первая вещь, которую мы сделаем - создадим копии двух рёберных списков, поскольку мы не хотим испортить списки в их оригинальном контексте. Список граней, который мы будем строить, инициализируется в пустой список, и мы проверяем разумность и равенство длин обоих рёберных списков. Если это подтверждается, мы приступаем к следующему куску:
for a in e1:
distance = None # расстояние
best = None # лучший
enot = [] # отвергнутые рёбра
Мы повторяем по каждому ребру в первом списке, ссылаясь на это ребро через a. параметр distance содержит расстояние до ближайшего ребра во втором рёберном списке, а best будет ссылкой на это ребро. enot - список, который копит все рёбра из второго списка, которые находятся на большем расстоянии, чем наилучшее.
В конце каждой итерации, enot будет содержать все рёбра из второго списка минус одно - которое мы считаем ближайшим. Затем мы переназначаем enot на второй список, таким образом второй список уменьшается на одно ребро с каждой итерацией. Мы заканчиваем, как только второй список рёбер будет исчерпан:
while len(e2):
b = e2.pop(0)
Текущее ребро из второго списка, которое мы рассматриваем, называется b. Для наших целей, мы определяем расстояние между a и b как сумму расстояний между соответствующими вершинами в a и b. Также мы проверяем, не окажется ли короче сумма расстояний до перевёрнутых вершин b. Если получилась такая ситуация, мы меняем вершины в ребре b. Это может казаться сложным способом действий, но суммированием двух расстояний мы гарантируем, что рёбра, которые сравнительно коллинеарны (параллельны) - привилегированы, тем самым уменьшая число неплоских граней, которые будут созданы. Проверяя, не приведёт ли перевёрнутый второй край к более короткому расстоянию, мы предотвращаем образование искорёженного в виде галстука-бабочки четырёхугольника, как проиллюстрировано на следующем рисунке:
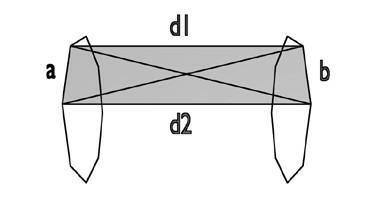
Реализация будет выглядеть похоже на предшествующий рисунок, где выделенные вектора - псевдонимы на объект Mathutil.Vector, преобразующий наши кортежи с координатами x, y, и z в соответствующие векторы, которые мы можем вычитать, складывать, и получать их длину.
Сначала мы вычисляем расстояние:
d1 = (vec(verts[a[0]]) - vec(verts[b[0]])).length +
(vec(verts[a[1]]) – vec(verts[b[1]])).length
Затем мы проверяем с перевёрнутым ребром b, будет ли в результате расстояние короче:
d2 = (vec(verts[a[0]]) - vec(verts[b[1]])).length +
(vec(verts[a[1]]) - vec(verts[b[0]])).length
if d2<d1 :
b =(b[1],b[0])
d1 = d2
Если рассчитанное расстояние не самое короткое, мы откладываем ребро для следующей итерации, если оно не первое, с которым мы столкнулись:
if distance == None or d1<distance :
if best != None:
enot.append(best)
best = b
distance = d1
else:
enot.append(b)
Список отклонённых рёбер становится новым e2, затем мы заполняем список граней новой парой рёбер, и переходим к новой итерации по первому списку рёбер (a) – доп. пер.
e2 = enot
faces.append((a,best))
Наконец, мы преобразуем наш список граней, состоящий из кортежей двух рёбер, в список кортежей из четырех индексов:
return [(a[0],b[0],b[1],a[1]) for a,b in faces]
Есть много больше в этом скрипте, и мы вновь будем рассматривать creepycrawlies.py в следующей главе, где мы добавим модификаторы, группы вершин и арматуру к нашей модели. Иллюстрация показывает образцы бестиария, которые могут быть созданы скриптом.
