Выбор искривлённых (не-планарных) четырёхугольников

Выбор искривлённых (не-планарных) четырёхугольников

Искривлённые четырёхугольники (Warped quads), также известные как "а-ля галстук-бабочка" (bow-tie quads), иногда формируюся случайно при спутанном порядке вершин во время создания грани. В менее экстремальных случаях они могут быть созданы при перемещении одной вершины плоского четырёхугольника. Эта небольшая иллюстрация показывает, как они могут выглядеть в 3D-виде:

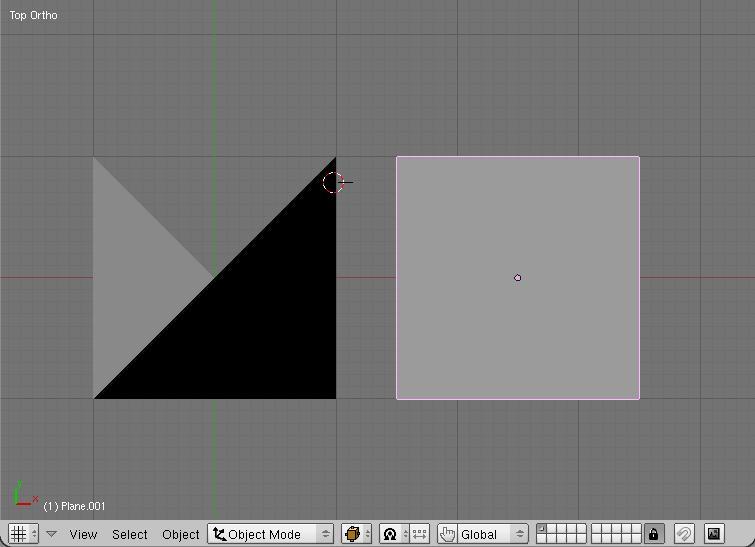
В 3D-виде, искривлённая грань справа не кажется необычной, но на рендере она не покажет однородного затенения:

Оба объекта являются плоскостями (plane) и состоят из единственной грани с четырьмя вершинами. Тот, что слева - четырёхугольник галстук-бабочка. Его правый край перевёрнут на полные 180 градусов, в результате появляется безобразный черный треугольник, где мы видим обратную сторону искривленной грани. Плоскость справа не показывает никакого заметного искажения в 3D-виде, хотя его правая верхняя вершина перемещена на значительное расстояние вдоль оси z (по линии нашего взгляда). При рендере, тем не менее, искажение правой плоскости ясно видимо. Видимое искажение немного искривленного четырёхугольника можно преодолеть, включив атрибут smooth у грани, который интерполирует вершинные нормали вдоль грани, тогда вид результата будет плавнее. Немного искривленные четырёхугольники почти неизбежны при моделировании или деформации меша арматурой, а могут ли они привести к видимым проблемам, зависит от ситуации. Часто бывает полезно, если вы можете найти и выбрать их, чтобы вынести ваше собственное решение.

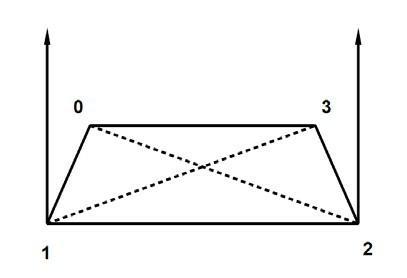
Искривлённый четырёхугольник можно идентифицировать, проверяя, что независимые нормали треугольников, которые формируют четырёхугольник, указывают в одинаковом направлении. Плоский четырёхугольник будет иметь нормали треугольников, направленные в одном и том же направлении, как показано на следующей картинке:

В то время как в искривлённом четырёхугольнике эти нормали не параллельны:

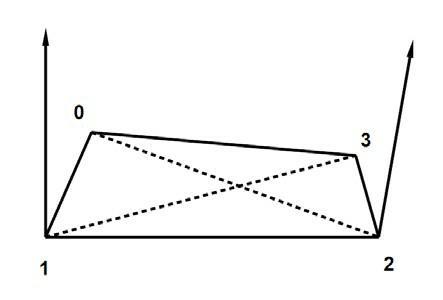
Эти нормали треугольников - не то же самое, что вершинные нормали: те определены как среднее всех нормалей граней, использующих вершину, так что мы должны вычислить самостоятельно эти нормали треугольников. Это можно сделать посредством вычисления векторного произведения рёберных векторов, то есть, векторов, определенных двумя вершинами в конце каждого ребра. В показанных у нас примерах есть левый треугольник, его нормаль формируется взятием векторного произведения рёберных векторов 1?0 и 1? 2, и треугольник справа, для него вычисляем векторное произведение рёберных векторов 2?1 и 2?3.

Не имеет значения, просматриваем мы наши рёбра по часовой стрелке или против часовой стрелки, но мы должны быть осторожными, чтобы последовательно упорядочивать рёбра при расчете векторных произведений, поскольку знак может поменяться. Как только у нас будут наши нормали треугольников, мы можем проверить, указывают ли они в одном и том же направлении, удостоверившись, что все компоненты (х, у, и z) одного вектора масштабированы одинаково по сравнению с соответствующими компонентами второго вектора. Тем не менее, чтобы дать нам отчасти большую гибкость, мы хотели бы вычислять угол между нормалями треугольников и выбирать грань, только если этот угол превышает некоторый минимум. Нам не нужно самим разрабатывать такую функцию, поскольку модуль Blender.Mathutils предоставляет функцию AngleBetweenVecs().

Возможно построить четыре различных треугольника в четырёхугольнике, но не нужно сравнивать их все - нормалей любых двух треугольников будет достаточно, поскольку перемещение одной вершины в четырёхугольнике изменит нормали трёх из четырех возможных треугольников.

Схема и код выбора искривлённых граней

Вооружившись всей этой информацией, набросаем схему для нашего инструмента, она будет выглядеть так:

1. Показать всплывающий диалог для ввода минимального угла.

2. Проверить, что активный объект - это меш, и он в режиме

редактирования.

3. Включить режим выбора граней

4. Для всех граней проверить, является ли она четырёхугольником, и если так:

• Вычислить нормаль треугольника, определенного вершинами 0, 1, и 2

• Вычислить нормаль треугольника, определенного вершинами 1, 2, и 3

• Вычислить угол между нормалями

• Если угол > минимального угла, выбрать грань Это транслируется в следующий код для фактического обнаружения и выбора (полный скрипт предоставлен как

warpselect.py):

def warpselect(me,maxangle=5.0):

    for face in me.faces:

        if len(face.verts) == 4:

            n1 = (face.verts[0].co -

                  face.verts[1].co ).cross( 

                  face.verts[2].co - face.verts[1].co )

            n2 = ( face.verts[1].co -

                  face.verts[2].co ).cross( 

                  face.verts[3].co - face.verts[2].co )

            a = AngleBetweenVecs(n1,n2)

            if a > maxangle :

                face.sel = 1

Как Вы можете видеть, наша схема почти взаимно-однозначно соответствует коду. Заметьте, что AngleBetweenVecs() возвращает угол в градусах, так что мы можем непосредственно сравнить его с maxangle, который тоже выражен в градусах. Также, нет необходимости самостоятельно выполнять само векторное произведение двух векторов, так как класс Vector в Блендере хорошо снабжен всеми видами операторов. Прежде, чем мы сможем вызвать эту функцию, мы должны позаботиться о важной детали: для того, чтобы выбирать грани, должен быть включен режим выбора граней. Это можно сделать следующим образом:

selectmode = Blender.Mesh.Mode()

Blender.Mesh.Mode(selectmode |

Blender.Mesh.SelectModes.FACE)

Чтобы проиллюстрировать малоизвестный факт о том, что режимы выбора не являются взаимоисключающими, мы установили режим выбора граней дополнительно к любому уже выбранному режиму двоичным объединением величин или оператором (|). В конце скрипта мы восстанавливаем режим, который был активен.