11.2. СВОЙСТВА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

11.2. СВОЙСТВА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

Следует выделить следующие свойства программного обеспечения.

Корректность программного обеспечения — свойство безошибочной реализации требуемого алгоритма при отсутствии таких мешающих факторов, как ошибки входных данных, ошибки операторов ЭВМ (людей), сбои и отказы ЭВМ.

В интуитивном смысле под корректностью понимают свойства программы, свидетельствующие об отсутствии в ней ошибок, допущенных разработчиком на различных этапах проектирования (спецификации, проектирования алгоритма и структур данных, кодировании). Корректность самой программы понимают по отношению к целям, поставленным перед ее разработкой (т. е. это относительное свойство).

Устойчивость — свойство осуществлять требуемое преобразование информации при сохранении выходных решений программы в пределах допусков, установленных спецификацией. Устойчивость характеризует поведение программы при воздействии на нее таких факторов неустойчивости, как ошибки операторов ЭВМ, а также не выявленные ошибки программы.

Восстанавливаемость — свойство программного обеспечения, характеризующее возможность приспосабливаться к обнаружению ошибок и их устранению.

Надежность можно представить совокупностью следующих характеристик:

— целостностью программного средства (способностью его к защите от отказов);

— живучестью (способностью к входному контролю данных и их проверки в ходе работы);

— завершенностью (бездефектностью готового программного средства, характеристикой качества его тестирования);

— работоспособностью (способностью программного средства к восстановлению своих возможностей после сбоев).

Отличие понятия корректности и надежности программ состоит в следующем:

— надежность характеризует как программу, так и ее "окружение" (качество аппаратуры, квалификацию пользователя и т. п.);

— говоря о надежности программы, обычно допускают определенную, хотя и малую долю ошибок в ней и оценивают вероятность их появления.

Вернемся к понятию корректности. Очевидно, что не всякая синтаксически правильная программа является корректной в указанном выше смысле, т. е. корректность характеризует семантические свойства программ.

С учетом специфики появления ошибок в программах можно выделить две стороны понятия корректности:

— корректность как точное соответствие целям разработки программы (которые отражены в спецификации) при условии ее завершения или частичная корректность;

— завершение программы, т. е. достижение программой в процессе ее выполнения своей конечной точки.

В зависимости от выполнения или невыполнения каждого из двух названных свойств программы различают шесть задач анализа корректности:

1) доказательство частичной корректности;

2) доказательство частичной некорректности;

3) доказательство завершения программы;

4) доказательство не завершения программы;

5) доказательство тотальной (полной) корректности (т. е. одновременное решение 1-й и 3-й задач);

6) доказательство некорректности (решение 2-й или 4-й задачи). Методы доказательства частичной корректности программ, как

правило, опираются на аксиоматический подход к формализации семантики языков программирования. Аксиоматическая семантика языка программирования представляет собой совокупность аксиом и правил вывода. С помощью аксиом задается семантика простых операторов языка (присваивания, ввода-вывода, вызова процедур). С помощью правил вывода описывается семантика составных операторов или управляющих структур (последовательности, условного выбора, циклов). Среди этих правил вывода надо отметить правило вывода для операторов цикла, так как оно требует знания инварианта цикла (формулы, истинность которой не изменяется при любом прохождении цикла).

Наиболее известным из методов доказательства частичной корректности программ является метод индуктивных утверждений, предложенный Флойдом и усовершенствованный Хоаром. Один из важных этапов этого метода — получение аннотированной программы. На этом этапе для синтаксически правильной программы должны быть заданы утверждения на языке логики предикатов первого порядка: входной предикат; выходной предикат.

Эти утверждения задаются для входной точки цикла и должны характеризовать семантику вычислений в цикле.

Доказательство неистинности условий корректности свидетельствует о неправильности программы или ее спецификации, или программы и спецификации.

По влиянию на результаты обработки информации к надежности и устойчивости программного обеспечения близка и точность программного обеспечения, определяемая ошибками метода и ошибками представления данных.

Наиболее простыми методами оценки надежности программного обеспечения являются эмпирические модели, основанные на опыте разработки программ: если до начала тестирования на 1000 операторов приходится 10 ошибок, а приемлемым качеством является 1 ошибка, то в ходе тестирования надо найти:

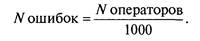
Более точна модель Холстеда: N ошибок = N операторов * log₂(N операторов — N операндов),

где N операторов — число операторов в программе; N операндов — число операндов в программе.

Эмпирическая модель фирмы IBM:

N ошибок = 23 M(10) + 2 M(1),

где M(10) — число модулей с 10 и более исправлениями; M(1) — число модулей с менее 10 исправлениями.

Если в модуле обнаружено более 10 ошибок, то его программируют заново.

По методу Милса в разрабатываемую программу вносят заранее известное число ошибок. Далее считают, что темпы выявления ошибок (известных и неизвестных) одинаковы.