Замена цепей при применении теоремы Тевенина

Замена цепей при применении теоремы Тевенина

Схема на рис. 1.11 показывает другие возможности применения теоремы Тевенина. В этой схеме величине RL присваивается ряд различных значений и предлагается вычислить ток и напряжение нагрузки для каждого из них. Мы убедились, что нагрузочное сопротивление может быть удалено из схемы вместо замены его резистором с очень большим сопротивлением.

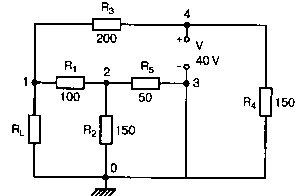
Рис. 1.11. Схема для замещения по теореме Тевенина 

Это можно еще раз проверить с помощью следующего входного файла:

Bridge-Circuit for Thevenin

V 4 3 40V

R1 1 2 100

R2 2 0 150

R3 1 4 200

R4 4 0 200

R5 2 3 50

.OP

.OPT nopage

.TF V(1) V

.END

Запустите анализ и нарисуйте по его результатам неидеальный источник напряжения Тевенина. Убедитесь, что вы обозначили все необходимые узлы. Результат должен соответствовать рис. 1.12. Выходные узлы обозначены как 1 и 0. Отметим, что напряжение холостого хода на узле 1 отрицательно относительно узла 0. PSpice дает для него значение V(1)=-2,9091 В. Команда .TF позволяет вычислить выходное сопротивление относительно V(1), равное 152,7 Ом, что соответствует значению сопротивления на рис. 1.13. Теперь мы можем изменять значение RL в широких пределах и проводить расчеты для каждого значения вручную.

**** 06/14/99 10:05:31 *********** Evaluation PSpice (Nov 1998) **********

Bridge Circuit for Thevenin

**** CIRCUIT DESCRIPTION

V 4 3 40V

R1 1 2 100

R2 2 0 150

R3 1 4 200

R4 4 0 200

R5 2 3 50 .OP

.ОРТ nopage

.TF V(1) V

.END

NODE VOLTAGE NODE VOLTAGE  NODE VOLTAGE  NODE VOLTAGE

( 1) -2.9091 ( 2) -13.0910 ( 3) -22.5450 ( 4) 17.4550

VOLTAGE SOURCE CURRENTS

NAME CURRENT

V   -1.891E-01

TOTAL POWER DISSIPATION 7.56E+00 WATTS

**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG С

**** SMALL-SIGNAL CHARACTERISTICS

V(1)/V = -7.273E-2

INPUT RESISTANCE AT V = 2.115E+02

OUTPUT RESISTANCE AT V(1) = 1.527E+02

Рис. 1.12. Выходной файл при моделировании схемы на рис. 1.11

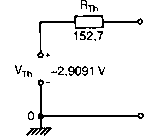
Рис. 1.13. Схема со значениями VTh и RTh для эквивалентного генератора Тевенина

Применение теоремы Тевенина позволило нам заменить сложную схему простым неидеальным генератором напряжения. И поскольку в этой схеме нет сопротивления нагрузки RL, не имеет значения, подключим ли мы его к реальной схеме или к эквивалентному генератору. Однако эти две схемы не вполне эквивалентны.

Вернемся, например, к схеме (рис. 1.8), с которой мы начали рассмотрение, при удаленном сопротивлении нагрузки VTh=50 В и RTh=216,7 Ом.

При RL=200 Ом ток составляет 0,12 А. Поскольку этот ток проходит через последовательную цепочку сопротивлений, мощность, потребляемая от источника VTh, составляет 6 Вт. Поскольку мощность нагрузки равна 2,88 Вт, оставшиеся 3,12 Вт выделяются на внутреннем сопротивлении RTh. Но в исходной схеме, напряжение источника равно 75 В и ток его составляет 0,33 А. Следовательно, от него потребляется мощность 24,8 Вт. Поскольку мощность, выделяемая в нагрузочном резисторе сопротивлением 200 Ом равна 2,88 Вт, оставшаяся часть мощности рассеивается на трех резисторах Т-образной схемы.

Этот пример показывает, что с энергетической точки зрения исходная схема и генератор Тевенина не эквивалентны.

Более 800 000 книг и аудиокниг! 📚

Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением

ПОЛУЧИТЬ ПОДАРОК

Данный текст является ознакомительным фрагментом.