Теорема Тевенина и ее применения

Теорема Тевенина и ее применения

Что представляет собой теорема Тевенина, и почему она так важна и так широко применяется? Если вы рассчитываете нетривиальные цепи и при этом хотите получить результат при различных нагрузочных сопротивлениях, то идеальным методом расчета и является применение теоремы Тевенина.

Схема на рис. 1.8(a) содержит источник напряжения и несколько резисторов, включая нагрузочный резистор R_L. Найдем напряжение на резисторе R_L и ток через него. Для этого можно найти эквивалентное сопротивление цепи, затем ток источника, падение напряжения на R₁ и так далее вплоть до падения напряжения на R_L. Однако если изменить сопротивление R_L, всю последовательность вычислений придется повторить. С помощью теоремы Тевенина эта проблема решается проще.

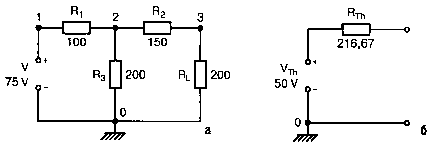
Рис. 1.8. К применению теоремы Тевенина: а — схема; б — источник эквивалентного напряжения и эквивалентное внутреннее сопротивление

Для начала удалим из схемы нагрузочное сопротивление. Этот метод не зависит от нагрузочного сопротивления, и это очень важно. Теперь найдем напряжение V₃₀, проще говоря, напряжение между узлами, к которым было подключено исключенное из схемы сопротивление нагрузки. Можно обозначить его как V_Th (Th — первые буквы имени Тевенина). Затем вычислим сопротивление схемы относительно этих же узлов, закоротив источник питания. Его можно обозначить как R_Th.

Заменим теперь схему неидеальным источником напряжения, содержащим идеальный источник V_Th с внутренним сопротивлением R_Th и вернем в полученную схему нагрузочное сопротивление R_L. Падение напряжения на этом резисторе и ток через него будут такими же, как в исходной схеме.

Найдем V_Th и R_Th для схемы рис. 1.8. Удалим R_L, затем используем выражение для делителя напряжения, чтобы вычислить V₂₀=50 В. Для определения R_Th закоротим источник V. Вычисляя теперь сопротивление относительно узлов 3 и 0, получим R_Th=216,67 Ом. Неидеальный источник напряжения состоит из включенных последовательно V_Th и R_Th, рис. 1.8(б). Для новой схемы гораздо проще получить значения тока и напряжения на нагрузке при любом значении R_L. Например, при R_L=200 Ом найдем, применяя выражение для делителя напряжения, V₃₀=24 В, а при R_L=300 Ом получим V₃₀=29 В.