Определение полного входного сопротивления в цепях переменного тока

Определение полного входного сопротивления в цепях переменного тока

Рассмотрим «черный ящик», содержащий цепь с неизвестным полным сопротивлением, показанный на рис. 2.16. С помощью команды .PRINT вы можете вывести и V(I), и I(R). Однако эта команда не позволяет вывести значение V(I)/I(R). Различные математические операторы в ней не допускаются. Чтобы получить график желаемой переменной, следует использовать функцию Probe, которая может, кроме того, строить функции, использующие следующие операторы:

abs(x) |x| sgn(x) +1 (если x > 0), 0 (если x = 0), -1 (если x<0) sqrt(x) ?x exp(x) ex log(x) ln(|x|) log10(x) log(| x|) m(x) модуль x p(x) фазовый угол x r(x) действительная часть x img(x) мнимая часть x g(x) групповая задержка от x pwr(x, y) |х|y sin(x) sin(x) cos(x) cos(x) tan(x) tg(x) atan(x) arctg(x) arctan(x) arctg(x) d(x) дифференциал от x s(x) интеграл от x avg(x) среднее значение от x rms(x) действующее значение от х min(x) минимум действительной части х max(х) максимум действительной части х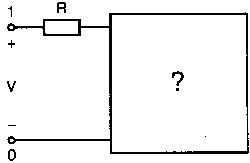

Рис. 2.16. Чёрный ящик, содержащий цепь с неизвестным полным сопротивлением

Таким образом, чтобы найти входное полное сопротивление схемы (рис. 2.16), можно включить очень маленький резистор R в качестве датчика тока. Полное входное сопротивление V(1)/I(R) можно найти в Probe, используя выражения r(V(I)/I(R)) для вещественной части Z и img(V(I)/I(R)) для мнимой части. Это дает тот же результат, что и использование r(VM(I)/IM(R)) и img(VM(I)/IM(R)). Получить фазовый угол для Z можно, используя p(V(I)/I(R)). Поясним эту методику примером.

На рис. 2.17 показана схема с резистивным датчиком тока и «неизвестным» полным сопротивлением в «черном ящике». Чтобы найти полное сопротивление, необходимо провести моделирование и использовать Probe.

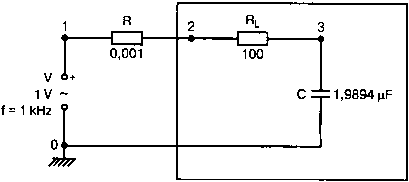
Рис. 2.17. Схема с резистивным датчиком тока

Во входном файле предусмотрена вариация частоты входного напряжения:

Input Impedance Using a Small Current-Sensing Resistor

V 1 0 AC 1V

R 1 2 0.001; Это резистивный датчик тока (шунт)

RL 2 3 100

RA 1 1А 1

С 3 0 1.9894uF

.AC LIN 501 500Hz 1500Hz

.PROBE 

.END

Проведите моделирование, и получите в Probe графики частотных зависимостей для действительной и мнимой частей Zin. Результаты показаны на рис. 2.18. Используя режим курсора, убедитесь, что при f=1 кГц получаются следующие значения сопротивления: Rin=100 Ом (действительная часть Zin) и Xin=-80 Ом (мнимая часть Zin).

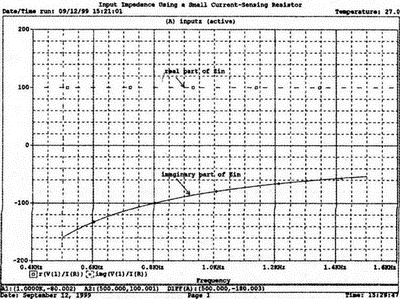
Рис. 2.18. Частотные зависимости для активной и реактивной составляющих Zin 

Более 800 000 книг и аудиокниг! 📚

Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением

ПОЛУЧИТЬ ПОДАРОК

Данный текст является ознакомительным фрагментом.