12.1. Гранные поверхности и многогранники

12.1. Гранные поверхности и многогранники

Гранные поверхности — поверхности, образованные перемещением прямолинейной образующей по направляющей, представляющей собой ломаную линию. На рис. 12.1 показан пример пирамидальной и призматической поверхностей.

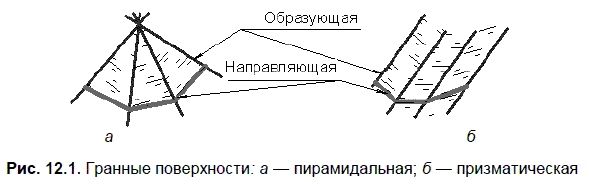
Пирамидальная поверхность образована движением прямолинейной образующей по ломаной направляющей, при этом одна точка, S — вершина образующей, неподвижна.

Призматическая поверхность образована движением прямолинейной образующей по ломаной направляющей, при этом образующая перемещается параллельно некоторому наперед заданному направлению.

Многогранники — замкнутые поверхности, образованные некоторым количеством граней.

Выпуклый многогранник расположен по одну сторону плоскости каждой грани многогранника. Сами грани также являются выпуклыми многогранниками.

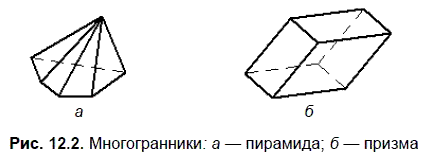
Пирамида (рис. 12.2, а) — многогранник, у которого одна грань, принимаемая за основание, является многоугольником, а остальные грани (боковые) — треугольники с общей точкой S, называемой вершиной.

В зависимости от числа вершин у многоугольника основания, пирамиду называют: треугольной, если в основании треугольник; четырехугольной, если в основании четырехугольник, и т. д.

Правильная пирамида имеет в основании правильный многоугольник, с центром которого совпадает высота правильной пирамиды. Если пирамида является правильной, то в нее или около можно вписать или описать сферу, центр которой лежит на высоте пирамиды.

Призма (рис. 12.2, б) — многогранник, у которого две грани — основания являются одинаковыми и взаимно параллельными многоугольниками, а остальные грани (боковые) — четырехугольниками.

Прямая призма имеет боковые ребра, которые перпендикулярны основанию.

Правильная призма — это прямая призма, у которой основания — правильные многоугольники.

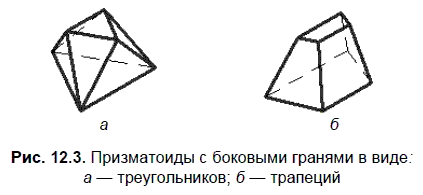
Призматоид — многогранник, у которого параллельные основания являются многоугольниками с произвольным числом углов, боковые грани — треугольники (рис. 12.3, а) или трапеции (рис. 12.3, б).

Правильные многогранники имеют все грани в виде правильных и конгруэнтных многоугольников, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней.

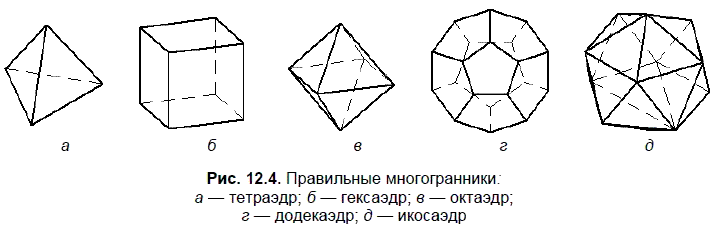
Гранями правильных многогранников могут быть только правильные треугольники, четырехугольники и пятиугольники. Одной из особенностей правильных многогранников является то, что каждый из них вписывается в сферу. Примерами правильных многогранников являются:

? тетраэдр — правильный четырехгранник (рис. 12.4, а);

? гексаэдр — правильный шестигранник (рис. 12.4, б);

? октаэдр — правильный восьмигранник (рис. 12.4, в);

? додекаэдр — правильный двенадцатигранник (рис. 12.4, г);

? икосаэдр — правильный двадцатигранник (рис. 12.4, д).

Данный текст является ознакомительным фрагментом.