2.3. Представление чисел в компьютере
2.3. Представление чисел в компьютере
Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.
Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 110011012 будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2n – 1, где п – число разрядов числа. Максимальное число при этом будет равно 28 – 1 = 25510 = 111111112и минимальное 010 = 000000002. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 25510.
В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 53610 = 00000010000110002 будет представлено в регистрах памяти в следующем виде:

а отрицательное число -53610 = 10000010000110002 в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2n-1 – 1 = 216-1 – 1 = 215 – 1 = 3276710 = 1111111111111112 и диапазон чисел будет находиться в пределах от -3276710 до 32767.
Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.
Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:
1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;
2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);
3) к полученному обратному коду прибавить единицу к младшему разряду.
Например, для числа -53610 в таком формате модуль будет равен 00000010000110002, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -53610, т. е. число 53610, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -53610 и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.
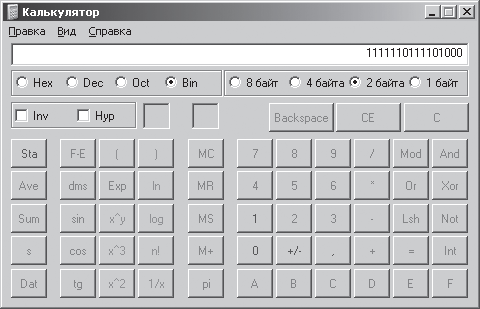
Рис. 2.6. Результат получения дополнительного кода
Необходимо помнить, что дополнительный код положительного числа – само число.
Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(231 – 1) … + 231 – 1 и -(263-1) … + 263 – 1.
Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).
Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.
Выражение (2.7) для десятичной системы счисления примет вид:

для двоичной —

для восьмеричной —
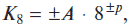
для шестнадцатеричной —

и т. д.
Такая форма представления числа также называется нормальной. С изменением порядка запятая в числе смещается, т. е. как бы плавает влево или вправо. Поэтому нормальную форму представления чисел называют формой с плавающей запятой. Десятичное число 15,5, например, в формате с плавающей запятой может быть представлено в виде: 0,155 · 102; 1,55 · 101; 15,5 · 100; 155,0 · 10-1; 1550,0 · 10-2 и т. д. Эта форма записи десятичного числа 15,5 с плавающей запятой не используется при написании компьютерных программ и вводе их в компьютер (устройства ввода компьютеров воспринимают только линейную запись данных). Исходя из этого выражение (2.7) для представления десятичных чисел и ввода их в компьютер преобразовывают к виду

где Р – порядок числа,
т. е. вместо основания системы счисления 10 пишут букву Е, вместо запятой – точку, и знак умножения не ставится. Таким образом, число 15,5 в формате с плавающей запятой и линейной записи (компьютерное представление) будет записано в виде: 0.155Е2; 1.55Е1; 15.5Е0; 155.0Е-1; 1550.0Е-2 и т.д.
Независимо от системы счисления любое число в форме с плавающей запятой может быть представлено бесконечным множеством чисел. Такая форма записи называется ненормализованной. Для однозначного представления чисел с плавающей запятой используют нормализованную форму записи числа, при которой мантисса числа должна отвечать условию

где |А| — абсолютное значение мантиссы числа.
Условие (2.9) означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля, или, другими словами, если после запятой в мантиссе стоит не нуль, то число называется нормализованным. Так, число 15,5 в нормализованном виде (нормализованная мантисса) в форме с плавающей запятой будет выглядеть следующим образом: 0,155 · 102, т. е. нормализованная мантисса будет A = 0,155 и порядок Р = 2, или в компьютерном представлении числа 0.155Е2.
Числа в форме с плавающей запятой имеют фиксированный формат и занимают в памяти компьютера четыре (32 бит) или восемь байт (64 бит). Если число занимает в памяти компьютера 32 разряда, то это число обычной точности, если 64 разряда, то это число двойной точности. При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, мантиссы и порядка. Количество разрядов, которое отводится под порядок числа, определяет диапазон изменения чисел, а количество разрядов, отведенных для хранения мантиссы, – точность, с которой задается число.
При выполнении арифметических операций (сложение и вычитание) над числами, представленными в формате с плавающей запятой, реализуется следующий порядок действий (алгоритм) :
1) производится выравнивание порядков чисел, над которыми совершаются арифметические операции (порядок меньшего по модулю числа увеличивается до величины порядка большего по модулю числа, мантисса при этом уменьшается в такое же количество раз);
2) выполняются арифметические операции над мантиссами чисел;
3) производится нормализация полученного результата.
Поясним сказанное выше на примерах.
Пример 1
Произведем сложение двух чисел 0,5 · 102 и 0,8 · 103 в формате с плавающей запятой.
Решение.
Проведем выравнивание порядков и сложение мантисс 0,05 · 103 + 0,8 · 103 = 0,85 · 103. Полученная мантисса 0,85 является нормализованной, так как удовлетворяет условию (2.9).
Пример 2
Произведем сложение двух чисел 0,1 · 22 и 0,1 · 23 в формате с плавающей запятой.
Решение.
Проведем выравнивание порядков и сложение мантисс: 0,01 · 23 + 0,1 · 23 = 0,11 · 23. Полученная мантисса 0,11 является нормализованной, так как удовлетворяет условию (2.9).
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
5.1. Поиск на локальном компьютере
5.1. Поиск на локальном компьютере Самой простой задачей поиска является поиск на локальном компьютере. В этом случае множество проблем решается автоматически, и вам остается разобраться с несколькими оставшимися: где и как искать.Если вы точно или хотя бы приблизительно
Получение сведений о компьютере
Получение сведений о компьютере С помощью базы данных CIMOM можно также определить конфигурацию операционной системы. Метод определения конфигурации подобен методу определения установленных на компьютере компонентов, поэтому будет рассмотрена лишь часть кода, с помощью
3. Представление чисел в ЭВМ
3. Представление чисел в ЭВМ 32-разрядные процессоры могут работать с оперативной памятью емкостью до 232-1, а адреса могут записываться в диапазоне 00000000 – FFFFFFFF. Однако в реальном режиме процессор работает с памятью до 220-1, а адреса попадают в диапазон 00000 – FFFFF. Байты памяти
3.1.1. Аппаратное представление целых чисел
3.1.1. Аппаратное представление целых чисел Delphi относится к языкам, в которых целые типы данных максимально приближены к аппаратной реализации целых чисел процессором. Это позволяет выполнять операции с целочисленными данными максимально быстро, но заставляет
5.1. Представление чисел в языке Ruby
5.1. Представление чисел в языке Ruby Если вы знакомы с любым другим языком программирования, то представление чисел в Ruby не вызовет у вас никакого удивления. Объект класса Fixnum может представлять число со знаком или без знака:237 # Число без знака (положительное).+237 # То же, что
11.20. Представление больших чисел фиксированного размера
11.20. Представление больших чисел фиксированного размера ПроблемаТребуется выполнить операции с числами, размер которых превышает размер типа long int.РешениеШаблон BigInt в примере 11.38 использует bitset из заголовочного файла <bitset> для того, чтобы можно было представить целые
Преобразования чисел
Преобразования чисел В случае встроенных числовых типов (sbyte, int, float и т.д.) явное преобразование требуется тогда, когда вы пытаетесь сохранить большее значение в меньшем контейнере, поскольку при этом может происходить потеря данных. По сути, это способ сказать
СОРТИРОВКА ЧИСЕЛ
СОРТИРОВКА ЧИСЕЛ Одним из наиболее распространенных тестов для машин является сортировка. Мы хотим разработать программу для сортировки целых чисел. Снова применим принцип черного ящика и подумаем в терминах ввода и вывода. Наш общий замысел, показанный на рис. 10.4,
Воспроизведение звука на компьютере
Воспроизведение звука на компьютере Воспроизведение цифрового звука – процесс, обратный оцифровке. Устройство, входящее в состав звуковой карты компьютера, – цифроаналоговый преобразователь (ЦАП) получает от программы-проигрывателя последовательность записей
Форматирование чисел
Форматирование чисел Мы уже познакомились с функцией языка XPath string, которая конвертирует свой аргумент в строку. Эта функция может преобразовать в строку и численное значение, но возможности ее при этом сильно ограничены.К счастью, XSLT предоставляет мощные возможности
1.1. Немного о компьютере
1.1. Немного о компьютере Во все времена человек пытался облегчить себе выполнение тех или иных работ, в результате чего появлялись различные приспособления. Однако процессы становились все сложнее, и существующие механизмы уже не справлялись со своими задачами и не
Настройка соединения на компьютере
Настройка соединения на компьютере Настройка компьютера заключается в установке и настройке модема и настройке удаленного соединения. В нашем случае установка модема означает только установку его драйвера. Драйвер может быть найден и установлен на ваш компьютер
Телевизор в компьютере
Телевизор в компьютере Тем пользователям, которые привыкли к постоянно работающему телевизору, полезной покажется возможность современного компьютера показывать телепрограммы на экране монитора.Действительно, можно настроить систему так, чтобы телепрограмма шла,
2. Представление чисел в ЭВМ. Формализованное понятие алгоритма
2. Представление чисел в ЭВМ. Формализованное понятие алгоритма 32-разрядные процессоры могут работать с оперативной памятью емкостью до 232-1, а адреса могут записываться в диапазоне 00000000 – FFFFFFFF. Однако в реальном режиме процессор работает с памятью до 220-1, а адреса
Исправляем ошибки на компьютере
Исправляем ошибки на компьютере Кадрирование Внимательно посмотрите на фотографию, представьте, что это не ваша работа, а снимок другого человека. Определите, без чего фото будет как минимум не хуже при сохранении сюжета, и смело кадрируйте — обрезайте и удаляйте все
Тренировать внимание на компьютере?
Тренировать внимание на компьютере? «Допустим, это верно в отношении телевидения. Но ведь есть исследования, которые показывают, что внимание можно даже тренировать на компьютере!» — возразят мне в этом месте те, кто охотно сидит перед компьютером и расстреливает