ПРИЛОЖЕНИЕ

ПРИЛОЖЕНИЕ

Вычислительная машина «Сетунь» Московского Государственного университета

Н. П. Брусенцов

Общая характеристика машины

Вычислительная машина «Сетунь» представляет собой автоматическую цифровую машину, предназначенную для решения научно-технических задач. Это одноадресная машина последовательного действия с фиксированным положением запятой.

Особенностью машины в математическом отношении является использование троичной системы счисления с коэффициентами 1, 0, –1.

В инженерном отношении машина примечательна тем, что в качестве основного элемента схем в ней применен магнитный усилитель с питанием импульсами тока. Такой усилитель состоит из нелинейного трансформатора с миниатюрным ферритовым сердечником и германиевого диода. Необходимые для реализации троичного счета три устойчивых состояния получаются с помощью пары усилителей. Общее число усилителей в машине — около четырех тысяч. Электронные лампы использованы в машине для генерирования импульсов тока, питающих магнитные усилители, и импульсов записи на магнитный барабан. Полупроводниковые триоды применены в схемах, обслуживающих матрицу запоминающего устройства на ферритовых сердечниках и в усилителях сигналов, считываемых с магнитного барабана.

Внутренние устройства машины работают на частоте 200 кГц, выполняя основные команды со следующими затратами времени: сложение — 180 мкс, умножение — 325 мкс, передача управления — 100 мкс.

Длина слова в арифметическом устройстве машины — 18 троичных разрядов. Команда кодируется полусловом, то есть девятью разрядами. В запоминающем устройстве каждая пара полуслов, составляющая полное слово, и каждое полуслово в отдельности наделены независимыми адресами. Число, представленное полусловом, воспринимается арифметическим устройством как 18-разрядное с нулями в младших разрядах.

Оперативное запоминающее устройство машины, выполненное на ферритовых сердечниках, обладает емкостью в 162 полуслова.

Запоминающее устройство на магнитном барабане вмещает 2268 полуслов. Обмен между барабаном и оперативным запоминающим устройством производится группами по 54 полуслова. Предполагается ввести дополнительное запоминающее устройство на магнитной ленте и увеличить емкость барабана до 4374 полуслов.

Ввод данных в машину производится с пятипозиционной бумажной перфоленты посредством фотоэлектрического считывающего устройства, а вывод на перфоленту и печать результатов — на стандартном рулонном телетайпе. Ввод и вывод информации осуществляется также группами по 54 полуслова.

В арифметическом устройстве машины «Сетунь» 18-разрядное троичное слово рассматривается как число, в котором запятая расположена между вторым и третьи разрядами. Это число можно выразить формулой

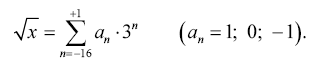
Диапазон чисел в арифметическом устройстве составляет –4,5 < х < +4,5 при абсолютной погрешности |?х| < 0,5 ? 3^–16. Число считается нормализованным, если оно заключено в интервале 0,5–1,5 или равно нулю. Порядок нормализованного числа изображается пятью старшими разрядами полуслова, хранящегося в запоминающем устройстве по отдельному адресу.

Девять разрядов полуслова, представляющего команду, распределены следующим образом: пять первых разрядов составляют адрес, три разряда — код операции, девятый разряд — признак модификации адреса. Если в этом разряде стоит 0, то команда выполняется без изменения адреса, если 1, то к адресу прибавляется число, находящееся в регистре модификации, если –1, то это число вычитается из адреса. Особое значение имеет младший (пятый) разряд адреса: у адреса полного слова в этом разряде –1, у адреса старшего полуслова 0, у адреса младшего полуслова 1.

В командах, относящихся к магнитному барабану или к устройствам ввода и вывода, первый разряд указывает, какая треть матрицы должна использоваться для записи (считывания) передаваемой информации. Остальные четыре разряда адресной части команды либо обозначают номер зоны на барабане, либо используются для конкретизации команды: ввод или вывод.

В функциональном отношении машина разделяется на шесть устройств:

1) арифметическое устройство;

2) устройство управления;

3) оперативное запоминающее устройство;

4) устройство ввода;

5) устройство вывода;

6) запоминающее устройство на магнитном барабане.

Преимущества троичной системы счисления

Главное преимущество троичного представления чисел перед принятым в современных компьютерах двоичной состоит не в иллюзорной экономности троичного кода, а в том, что с тремя цифрами возможен натуральный код чисел со знаком, а с двумя невозможен. Несовершенство двоичной арифметики и реализующих ее цифровых машин обусловлено именно тем, что двоичным кодом естественно представимы либо только неотрицательные числа, либо только неположительные, а для представления всей необходимой для арифметики совокупности — положительных, отрицательных и нуля — приходится пользоваться искусственными приемами типа прямого, обратного или дополнительного кода, системой с отрицательным основанием или с цифрами +1, –1 и другими ухищрениями.

В троичном коде с цифрами +1, 0, –1 имеет место естественное представление чисел со знаком (так называемая симметричная, уравновешенная или сбалансированная система), и «двоичных» проблем, не имеющих удовлетворительного решения, просто нет. Это преимущество присуще всякой системе с нечетным числом цифр, но троичная система — самая простая из них и доступна для технической реализации.

Арифметические операции в троичной симметричной системе практически не сложнее двоичных, а если учесть, что в случае чисел со знаком двоичная арифметика использует искусственные коды, то окажется, что троичная даже проще. Операция сложения всякой цифры с нулем дает в результате эту же цифру. Сложение +1 с –1 дает нуль. И только сумма двух +1 или двух –1 формируется путем переноса в следующий разряд цифры того же знака, что и слагаемые и установки в текущем разряде цифры противоположного знака. Пример:

111011101010

+

111011110100

_____________

101110011110

В трехвходном троичном сумматоре перенос в следующий разряд возникает в 8 ситуациях из 27, а в двоичном — в 4 из 8. В троичном сумматоре с четырьмя входами перенос также происходит только в соседний разряд.

Операция умножения еще проще: умножение на нуль дает нуль, умножение на 1 повторяет множимое, умножение на –1 инвертирует множимое (заменяет 1 на –1, а –1 на 1). Инвертирование есть операция изменения знака числа.

Следует учесть, что комбинационный троичный сумматор осуществляет сложение чисел со знаком, а вычитание выполняется им при инвертировании одного из слагаемых. Соответственно троичный счетчик автоматически является реверсивным.

Важным достоинством троичного симметричного представления чисел является то, что усечение длины числа в нем равносильно правильному округлению. Способы округления, используемые в двоичных машинах, как известно, не обеспечивают этого.