Наука: Проблемы 2000 года: P=?NP

We use cookies. Read the Privacy and Cookie Policy

Наука: Проблемы 2000 года: P=?NP

Автор: Сергей Николенко

Наверное, мало кто из людей, связанных с компьютерной индустрией, не слышал об этой задаче, занимающей центральное место в современной теоретической (и практической) информатике. За применениями ее возможного решения далеко ходить не нужно — они так разнообразны, что вряд ли мне удастся изложить их все. P и NP, за выяснение факта равенства или неравенства которых платят миллион — это так называемые сложностные классы алгоритмов. Понятие сложности алгоритма совсем не такое сложное, как некоторые алгоритмы. Попробую изложить его здесь более или менее строго, потратив на это константное время (сейчас поймете, что это такое) — как свое, так и читателей.

Предельно коротко и нестрого (зато интуитивно) классы P и NP можно описать так: P — это вычислительные задачи, которые легко решить; NP — задачи, для которых легко проверить, верно ли предполагаемое решение. Перейдем к более точным формулировкам.

Начнем с моделей вычислений. Математические модели компьютеров появились раньше, чем сами электронно-вычислительные машины, но задержка оказалась небольшой. В 1936 году Эмиль Пост (Emil Leon Post), а в 1937 году — Алан Тьюринг (Alan Turing) независимо друг от друга разработали теоретическую модель, которая легла в основу теории алгоритмов. Первый программируемый компьютер — механический агрегат под названием Z3 — был создан уже в 1941 году[ЭНИАК — отнюдь не первый компьютер. Сам ЭНИАК был завершен в 1946 году, но в то время программа, по которой он действовал, была «зашита» в железо, и для перепрограммирования ЭНИАКа нужно было менять его схемы]. Идеальный компьютер очень прост (таково общее свойство большинства полезных математических моделей). Он представляет собой бесконечную в одну сторону (пусть справа) ленту, по которой бегает одна-единственная головка. В каждой ячейке ленты может стоять ноль, единица или не стоять ничего. На каждом шаге выполнения алгоритма головка может сдвинуться влево, сдвинуться вправо либо записать в ячейку, над которой она находится, ноль или единицу. Программа для такой машины — это сколь угодно большой, но конечный набор состояний, каждому из которых соответствует некоторое действие, а также следующее состояние. Есть два выделенных состояния — исходное, в котором начинается работа программы, и специальное состояние СТОП, которое соответствует выходу из программы. Например, вот простая программа:

состояние 0:

прочесть то, что находится под головкой: если 0, перейти в состояние 1; если 1, перейти в состояние 2; если пусто, перейти в состояние СТОП;

состояние 1:

записать в текущую ячейку 1 и перейти в состояние 3;

состояние 2:

записать в текущую ячейку 0 и перейти в состояние 3;

состояние 3:

сдвинуть головку вправо и перейти в состояние 0.

Она бит за битом инвертирует двоичную строку, записанную на ленте (считаем, что изначально головка находится в крайней левой ячейке, с которой начинается запись числа), а когда строка заканчивается, заканчивает работу и программа.

Эта модель вычислений, получившая название машины Тьюринга, стала общепринятой (хотя Пост придумал свою модель на год раньше). На первый взгляд такой простой объект кажется недостаточным для того, чтобы описать все многообразие компьютерных архитектур, — но пока не известно ни одного алгоритма, который нельзя было бы реализовать на машине Тьюринга. В логике и информатике широко известно нестрогое утверждение (так называемый тезис Черча), которое гласит, что любой объект, отвечающий нашему интуитивному понятию алгоритма, можно реализовать в виде программы на машине Тьюринга. Контрпримеров к этому утверждению пока не обнаружено, и оно считается верным — хотя доказать его, разумеется, невозможно.

Теперь нам нужно научиться оценивать скорость работы различных алгоритмов, сравнивать их друг с другом. Один и тот же алгоритм будет на «Пентиуме» работать несравненно быстрее, чем на машине Тьюринга. Более того, процессор современного компьютера может получить данные из любой ячейки памяти, просто «заказав» соответствующей шине адрес ячейки. А единственной головке машины Тьюринга, чтобы добраться до далеких данных, нужно шаг за шагом пройти всю ленту… Неужели эти изменения не влияют на теоретические оценки времени работы алгоритма?

Разумеется, влияют. Однако во многих принципиальных вопросах теории вычислений, к которым относится и обсуждаемая нами проблема P=?NP, принято считать эквивалентными по сложности такие алгоритмы, время выполнения которых отличается друг от друга полиномиально — то есть на величину, не превосходящую Cn

, где n — объем входной информации («длина входа»), C и d — константы[Отметим, что в теории вычислений невозможно оценивать работу алгоритма иначе, как на бесконечных сериях задач. Для этого используется язык «больших и малых О», пришедший сюда из матанализа. Например, если говорят, что алгоритм выполняется за время O(n•log n) на данном множестве задач, это означает, что существует некоторая константа C, единая для этого множества задач и такая, что алгоритм решает каждую из них не больше, чем за C•n•log n операций, где n — объем начальных данных задачи]. Неформально говоря, в рамках этой теории любые алгоритмы, работающие с «полиномиальной скоростью», считаются быстрыми (хотя на практике время их работы может быть неприемлемо большим). Класс задач, для которых существуют алгоритмы, решающие их за время, полиномиальное от размера входа, и есть тот самый класс P, о котором идет речь в формулировке нашей проблемы.

К классу P принадлежат очень многие известные задачи, — каждый, кто открывал учебники по программированию, помнит, сколько там алгоритмов, работающих за полиномиальное время. В статье «Теория и практика сложности» («КТ» #603) я уже писал о том, что Леонид Хачиян доказал, что в классе P лежит даже кажущаяся неприступно сложной задача линейного программирования.

Однако понять, что такое P, — это еще цветочки. Труднее дать определение класса NP. Формально оно звучит так: это класс задач, которые решаются за полиномиальное время на так называемых недетерминированных машинах Тьюринга. Можно довольно наглядно охарактеризовать эти задачи, используя понятие машины с подсказкой, хоть это и потребует некоторых усилий.

Рассмотрим для примера задачу выяснения истинности высказывания «заданное число — составное» (то есть у него есть нетривиальные простые делители). Это вычислительно сложная задача (по крайней мере, считается таковой). Однако если нам дали подсказку — предложили кандидата на роль делителя данного числа, — то проверка правильности подсказки очень проста: достаточно по-школьному, в столбик, разделить число на предполагаемый делитель. Эта быстрая операция позволяет сразу заключить: если разделилось без остатка, значит, делитель найден и число действительно составное. В этом случае машина выдает ответ «да». Если же не разделилось — машина, по правилам игры, должна сказать «нет». Ее задача — не найти ответ, а проверить, верно ли, что данная ей подсказка — это правильный ответ. Машина имеет право ошибаться только в одну сторону: она может сказать «нет», если подсказка не подходит (но мы-то понимаем, что может подойти какой-нибудь другой делитель, просто именно этот оказался неправильным), но не имеет права принять неверную подсказку (сказать «да», если делитель-подсказка не делит данное число). Более того, если на самом деле ответ положительный, требуется, чтобы существовала подсказка, которую приняла бы машина (в нашем примере это условие выполнено). Итак, задача входит в класс NP, если существует машина Тьюринга, которая по данной ей подсказке сможет за полиномиальное время либо дать положительный ответ и не ошибиться, либо дать отрицательный ответ с возможной ошибкой; однако для каждого набора данных, ответ на который положителен, должна существовать подсказка, которую примет такая машина Тьюринга.

Некоторые из задач класса NP — так называемые NP-полные задачи — обладают удивительным свойством универсальности: любую задачу из класса NP можно «полиномиально свести» к любой из NP-полных задач[Свести задачу A к задаче B — это значит построить алгоритм, который будет работать за полиномиальное время и решать задачу A, но при этом будет иметь право строить задачи вида B и считать, что они решаются моментально (за один такт). Такого рода вычисления называются вычислениями с оракулом; в данном случае роль оракула выполняет машина, решающая задачу B. Кстати, вычисления с оракулом — отдельная очень интересная тема: если, например, обобщить вопрос P=NP на машины Тьюринга с оракулом, то можно найти такой оракул, для которого P с этим оракулом будет равно NP. Но можно найти и такой оракул, что это равенство будет неверно!]. Вот популярный пример NP-полной задачи: предположим, что в большой компании некоторые люди знакомы друг с другом. Требуется найти размер максимальной группы людей, в которой все будут друг с другом знакомы. Это так называемая задача поиска клики — максимального полного графа. Другой пример — задача коммивояжера: дан набор городов и расстояний между ними, требуется найти кратчайший маршрут, следуя которому можно посетить все города. Третий пример я уже приводил в упомянутой выше статье: это SAT (задача пропозициональной выполнимости), в которой по заданной булевской формуле требуется определить, истинна ли она хоть при каких-нибудь значениях переменных. Эта задача исторически была первой из известных NP-полных задач (ее полноту доказал Стивен Кук (Stephen Cook), и проблему P=?NP иногда в его честь называют проблемой Кука). Несмотря на эквивалентность всех NP-полных задач, на деле сводить одну из них к другой бывает весьма неэффективно. Поэтому лучшие алгоритмы-рекордсмены, да и вообще алгоритмы, предназначенные для практического применения, разрабатываются для каждой задачи отдельно.

Машины, работающие за полиномиальное время с подсказкой, кажутся гораздо мощнее, чем обычные машины без подсказки. Действительно, им нужно всего лишь проверить данный ответ, а обычной машине нужно его сначала найти. Однако вопрос о том, нельзя ли каждую недетерминированную машину Тьюринга превратить в детерминированную, до сих пор открыт. Собственно, это и есть знаменитая проблема равенства классов P и NP.

Учитывая сказанное выше об NP-полных задачах, проблема будет решена положительно, если найдется полиномиальный алгоритм хотя бы для одной NP-полной задачи. Но пока таковых нет даже в перспективе; более того, нет даже субэкспоненциальных алгоритмов (то есть тех, которые бы работали за время, меньшее 2 cn , но большее полиномиального — например, за 2 ? n~). Такие алгоритмы существуют только для задач, которые подозревают в том, что они занимают промежуточное положение — и не полиномиальные, и не NP-полные. Такова, например, проблема изоморфизма графов: по двум данным графам понять, можно ли перевести вершины одного графа в вершины другого так, чтобы ребра переходили в ребра. Впрочем, подозрения могут и не оправдаться: например, одним из самых громких результатов последних лет был полиномиальный алгоритм для задачи проверки числа на простоту. Примечательно, кстати, что проверка на простоту оказывается принципиально проще, чем разложение на множители[Возможно, это покажется менее странным, если напомнить, что сложность измеряется от длины входа. А длина входа в данном случае — это длина числа в двоичной записи, то есть примерно его логарифм. И алгоритм, чтобы быть полиномиальным от длины входа, должен быть логарифмическим от величины числа, которое нужно проверить на простоту].

Теперь, когда мы поняли формулировку задачи, перейдем к ее обсуждению.

Первое: почему она так сложна? Конечно, можно сказать «потому что вот уже полвека пытаются и никак не могут», но есть и более интересные и глубокие причины. Я уже упоминал в сноске, что если рассмотреть «классы с оракулами», то для разных оракулов ответ получится разным. Переход от обычных классов к классам с произвольными оракулами называется релятивизацией. Большинство существующих идей и методов доказательства теорем в теории сложности вычислений выдерживают релятивизацию, то есть могут быть обобщены на случай произвольного оракула. Стало быть, все эти идеи и методы для доказательства (не)равенства P и NP неприменимы! Более того, в 1996 году Александр Разборов (наш соотечественник, лауреат премии Неванлинны) и Стивен Рудих (Steven Rudich) ввели класс так называемых естественных доказательств и показали, что нет естественных доказательств, которые бы позволили доказать, что SAT не решается за полиномиальное время. Под впечатлением таких результатов некоторые математики начинают склоняться к тому, что несовпадение P и NP может оказаться недоказуемым в рамках существующей аксиоматики. В 2002 году проводился даже опрос на эту тему. Из ста исследователей на вопрос «как вы считаете, равны ли P и NP?» 61 ответил «нет», 9 — «да», 22 — «сомневаюсь» и 8 — «наверное, вопрос не зависит от существующей аксиоматики».

Второе: что будет следовать из различных решений этой задачи. Если P не равно NP, все в порядке. Небо не упадет на землю, Запад не сойдется с Востоком, а пришествие Зверя будет отложено до лучших времен. А вот если P=NP, то начнется такое… Практика показывает: на деле «полиномиальное» означает «относительно легко решаемое». И если появятся способы относительно быстро решать NP-полные проблемы — могут возникнуть очень серьезные проблемы уже вне математики. Например, современная практическая криптография, основанная на RSA или DES/AES, окажется бесполезной. К чему это приведет, любой человек, знакомый с тем, как нынче хранится защищенная информация (номер вашей банковской карточки, пароль к вашему почтовому ящику и т. п.), легко может себе представить. Кроме того, это повлечет за собой серьезные изменения в наших представлениях об иерархии сложностных классов: целый бесконечный набор классов, которые сейчас считаются разными — так называемая полиномиальная иерархия, — «схлопнется» до одного-единственного класса P, и многие другие весьма правдоподобные предположения окажутся неверными. И все же, в отличие от гипотезы Римана, здесь нельзя сбрасывать со счетов вероятность того, что классы окажутся равными: уже много открытий чудных приготовила нам теория сложности, и как знать — может быть, наша уверенность в том, что P не равно NP, — тоже не более чем иллюзия…

Подведем итоги. Проблема равенства или неравенства классов P и NP — одна из центральных проблем современной информатики. Как мы только что видели, на предположении о неравенстве этих классов держится очень большая часть повседневной практической безопасности каждого из нас. Так что миллион за такую проблему — совсем не много, пусть даже платят за любое из двух решений — что за «равно», что за «не равно»[Правда, я не знаю, заплатят ли миллион за доказательство того, что это (не)равенство нельзя доказать. Думаю, да]. А еще эта проблема, наверное, одна из самых доступных для понимания непрофессионального математика — что порождает поток дилетантских, очевидно неверных решений. Надеюсь, читатели «КТ» будут умнее и если уж и придумают решение, то такое, чтобы о нем стоило написать отдельную подробную статью, а лучше — книгу.

NP-полнота как генератор драйва

Cреди NP-полных задач есть и более веселые экземпляры, нежели упоминаемые в статье Сергея Николенко классические проблемы математики. Оказывается, точно такой же полнотой обладают и стратегии некоторых популярных игр. Самые яркие примеры: «Тетрис» и «Сапер» (он же «Минер», «Minesweeper»), пожирающие с одинаковым аппетитом что рабочее, что свободное время. Связаны ли гипнотизирующие свойства игр с (предполагаемым) отсутствием для них простого алгоритма победы — вопрос из области психологии, а психологи, как известно, не склонны к однозначным ответам. Но не так давно было строго математически доказано: нахождение полиномиальных алгоритмов для этих игр повлечет снятие вопросительного знака в гипотезе P=?NP, а стало быть, и падение современной криптографии (по крайней мере, концептуально). В этом смысле «Тетрис» и «Сапер» ничем не хуже зловещего коммивояжера, согласного двигаться лишь по наиболее дешевому маршруту.

NP-полны многие задачи, связанные с даже не с обычным, а с сильно упрощенным офлайновым «Тетрисом», когда поток фигурок, валящихся с потолка, заранее известен, а каждую фигурку можно переворачивать и двигать сколько угодно раз. Среди этих задач — максимизация числа заполненных строк, а также минимизация высоты, на которой в процессе игры находится самый верхний квадратик уже уложенных фигурок (подробнее см. работу исследователей из MIT, arXiv:cs:CC/0210020).

Очень красиво доказывается NP-полнота стратегического планирования для «Сапера». Стратегия в нем основана на решении такой задачи — выяснить, допустима ли заданная конфигурация игры, то есть расстановка цифр, флажков, открытых и закрытых квадратиков (игра идет на поле произвольного размера). Допустимость означает, что эта конфигурация действительно возникает при некотором начальном расположении мин. Именно проблема установления допустимости NP-полна, а доказательство получено путем сведения этой задачи к классической NP-полной проблеме SAT. Но самое интересное, разумеется, не «что», а «как».

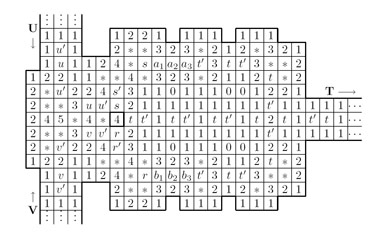
Ричард Кей из Университета Бирмингема (Richard Kaye) свел «Сапера» к SaT следующим образом. В SaT речь идет о поведении булевой формулы, то есть схемы, реализуемой гейтами вида "И", «ИЛИ», «НЕ». Кей придумал несколько экзотических конфигураций «Сапера», которые напрямую в самом буквальном смысле реализуют гейты и соединяющие их проводники. Из таких конфигураций можно собрать любую логическую схему. По сути, игровое поле превращается в компьютер! Квадраты поля принимают значения T (есть мина) или F (нет мины). Проверка допустимости конфигураций, реализующих логические и другие конструктивные элементы, интерпретируется как выполнение соответствующих им функций. На рис. 1 показано, как устроен провод, на рис. 2 — вентиль "И" (оригиналы рисунков см. на сайте Кея).

NP-полны также задачи составления самых обыкновенных расписаний для школьников и студентов (невзирая на это одна из российских компаний, легко находимая «Гуглом», предлагает программу составления расписаний, получившую призы на целом ряде конкурсов; суха теория, мой друг, но древо жизни пышно зеленеет, как говаривал один коварный литературный персонаж).

Таковы же и задачи оптимальной стратегии на рынке труда, частный случай которых — чисто математически, конечно, — подбор оптимальных супружеских пар по объявлениям. Короче говоря, что в игре, что в жизни примитивный (ну хорошо, полиномиальный) просчет ситуаций, что называется, не катит, и это отчасти обнадеживает.

Но только если P не равно NP!

Литература

[1] www.claymath.org/millennium/P_vs_NP

[2] en.wikipedia.org/wiki/Complexi-ty_classes_P_and_NP