Математические функции
Математические функции
Создайте чистую таблицу. Эту таблицу мы будем использовать для примеров использования функций.
Наиболее часто используемая функция в математических расчетах – это КОРЕНЬ.
1. Выделите ячейку R2C2. В эту ячейку мы будем вставлять функцию.
2. Нажмите кнопку Вставить функцию, расположенную в левой части строки формул. Появится диалоговое окно Мастер функций ? шаг 1 из 2 (рис. 6.6).
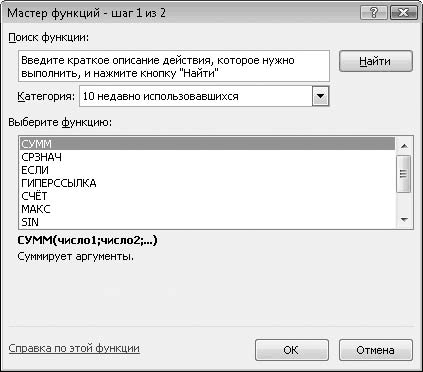
Рис. 6.6. Диалоговое окно Мастер функций – шаг 1 из 2
3. В раскрывающемся списке Категория выберите пункт Математические.
4. В списке Выберите функцию выберите пункт КОРЕНЬ. Обратите внимание, что в нижней части диалогового окна появляется краткое сообщение о назначении выбранной функции.
5. Нажмите кнопку ОК. Появится диалоговое окно Аргументы функции. В поле Число следует указать число или адрес ячейки, из значения которой следует извлечь корень (рис. 6.7).
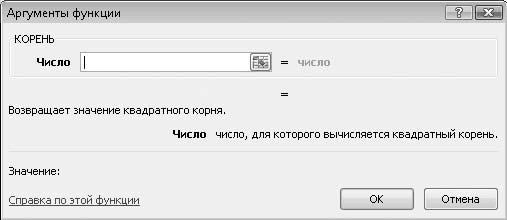
Рис. 6.7. Диалоговое окно Аргументы функции
ПРИМЕЧАНИЕ
Вы также можете воспользоваться кнопкой, расположенной в правой части поля Число, чтобы указать ячейку R1C1 мышью.
ПРИМЕЧАНИЕ
Вы можете не пользоваться диалоговым окном Мастер функций – шаг 1 из 2, а просто ввести в ячейку R2C2 следующий текст: =КОРЕНЬ(R1C1). Со временем, скорее всего, вы запомните часто используемые функции и в некоторых случаях будете вводить их вручную.
6. Введите в поле Число адрес ячейки R1C1. В эту ячейку мы будем подставлять числовые значения, из которых следует извлечь корень.
7. Нажмите кнопку ОК. Диалоговое окно закроется, а в ячейке R2C2 появится значение 0. Функция вернула значение 0, потому что ячейка R1C1 пуста.
8. Введите число 81 в ячейку R1C1 и нажмите клавишу Enter. В ячейке R2C2 появится число 9, которое является корнем числа 81.
Какое бы число вы ни подставляли в ячейку R1C1, ячейка R2C2 вернет вам корень этого числа. Если вы введете отрицательное число в ячейку R1C1, получите результат #ЧИСЛО!. Корень не может быть извлечен из отрицательного числа. Кроме того, сообщение об ошибке (#ЗНАЧ!) вы получите при попытке извлечь корень из текста.
В следующем примере мы переведем величину угла из градусов в радианы.
1. Очистите ячейку R2C2.
2. Нажмите кнопку Вставить функцию. В появившемся диалоговом окне в списке Выберите функцию щелкните кнопкой мыши на пункте РАДИАНЫ и нажмите кнопку ОК (убедитесь, что в диалоговом окне выбрана категория Математические).
3. В поле Число появившегося диалогового окна укажите адрес ячейки R1C1.
4. Нажмите кнопку ОК. Диалоговое окно будет закрыто, а в ячейке R2C2 появится значение ячейки R1C1, переведенное в радианы.
5. Введите в ячейку R1C1 число 180 и нажмите Enter. В ячейке R2C2 появится число 3,141593. Это – число ?. 180 градусов равняются числу ?.
Теперь рассмотрим функцию, предназначенную для округления числа. Допустим, у вас возникла необходимость округлить десятичную дробь с некоторым количеством символов после запятой до целого или до определенного количества знаков после запятой.
1. Очистите ячейку R2C2.
2. Нажмите кнопку Вставить функцию и выберите функцию ОКРУГЛ.
3. Нажмите кнопку ОК. Обратите внимание, что диалоговое окно Аргументы функции на этот раз содержит два поля (рис. 6.8). В первом поле следует указать число, которое требуется округлить (или адрес ячейки), а во втором (Число_разрядов) – количество знаков после запятой, до которого нужно округлить число.
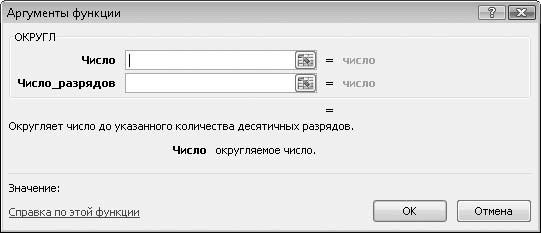
Рис. 6.8. Два аргумента в диалоговом окне Аргументы функции
ПРИМЕЧАНИЕ
Функция ГРАДУСЫ действует наоборот: переводит значение угла, указанное в радианах, в градусы.
4. В поле Число укажите адрес ячейки R1C1.
5. В поле Число_разрядов введите цифру 2. Мы округлим число до двух знаков после запятой.
6. Нажмите кнопку ОК. Диалоговое окно закроется.
7. В ячейку R1C1 введите число 3,151593 и нажмите клавишу Enter. В ячейке R2C2 появится число 3,15, то есть значение ячейки R1C1, округленное до двух знаков после запятой (рис. 6.9).
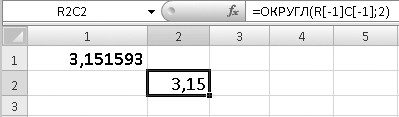
Рис. 6.9. Функция возвращает число ячейки R1C1, округленное до сотой доли
Вы можете править аргументы функции, не прибегая к диалоговому окну Мастер функций ? шаг 1 из 2. Изменим аргументы функции, чтобы она округляла значение ячейки R1C1 до четырех знаков после запятой.
1. Выделите ячейку R2C2 и посмотрите на строку формул. После адреса ячейки R1C1 (или ее относительного адреса) через точку с запятой указана цифра 2. Это и есть аргумент функции, указывающий количество знаков после запятой в результате округления.
2. Исправьте аргумент 2 в строке формул на 4 и нажмите клавишу Enter. В ячейке R2C2 появится значение 3,1516.
Таким образом, вы можете править аргументы функции прямо в строке формул.
Иногда возникает необходимость преобразовать арабские цифры и числа в римские. В программе Excel предусмотрена и такая функция.
1. Очистите ячейку R2C2.
2. Откройте диалоговое окно Мастер функций ? шаг 1 из 2 и выберите функцию РИМСКОЕ.
3. Нажмите клавишу Enter, в появившемся диалоговом окне укажите адрес ячейки R1C1 и нажмите кнопку ОК. В ячейке R2C2 появилась римская цифра III. Римские цифры не имеют дробной части, а поскольку в ячейке R1C1 было указано число 3,151593, функция вернула нам целую часть этого числа в римском формате.
4. В ячейку R1C1 введите число 15 и нажмите клавишу Enter. В ячейке R2C2 появится число XV.
5. Усложним задачу. Введите в ячейку R1C1 число 1145 и нажмите клавишу Enter. Как видите, функция справилась и с этой задачей и вернула число MCXLV.
Вы можете использовать функцию для получения случайного числа. Для этого следует указать два числа, и функция вернет вам случайное число в диапазоне этих чисел.
1. Очистите ячейку R2C2, откройте диалоговое окно Мастер функций ? шаг 1 из 2 и выберите функцию СЛУЧМЕЖДУ.
2. В диалоговом окне Аргументы функции следует указать нижнюю и верхнюю границу числа в соответствующих полях. В поле Нижн_граница укажите адрес ячейки R1C1, а в поле Верхн_граница – R1C2.
3. Закройте диалоговое окно и в ячейках R1C1 и R1C2 укажите два разных числа, например 1 и 6. В ячейке R2C2 появится случайное число от 1 до 6.
Вышеуказанная функция может заменить, например, игральные кубики.
Вы можете поэкспериментировать с остальными математическими функциями самостоятельно. Подсказка в диалоговом окне Мастер функций ? шаг 1 из 2 достаточно четко описывает назначение выбранной функции, а также вы можете воспользоваться ресурсами справочной системы программы, щелкнув кнопкой мыши на ссылке Справка по этой функции, расположенной в нижней части диалогового окна.
Данный текст является ознакомительным фрагментом.