Ввод трехмерных координат

Ввод трехмерных координат

При построении трехмерных объектов можно использовать те же способы задания координат, которые применяются при двухмерном моделировании. Отличительной особенностью указания пространственных координат является лишь то, что к осям X и Y, используемым ранее, добавляется еще и ось Z, проходящая перпендикулярно плоскости XY. Поэтому положение точек теперь будет определяться тремя координатами: x, y и z

Что касается полярных координат, применяемых в двухмерных чертежах, то в трехмерном пространстве их аналогами являются цилиндрические и сферические координаты. Кроме того, задавать координаты можно и в интерактивном режиме, то есть указывая их непосредственно на чертеже с помощью мыши.

Декартовы координаты

В трехмерном пространстве декартовы координаты имеют формат @X,Y,Z. Как видно, прямоугольные координаты почти так же указывались и в двухмерном пространстве – только добавилась третья координата. Напомним, что символа @ может и не быть, тогда положение точки будет задано относительно начала текущей системы координат – абсолютные координаты. Если же этот символ присутствует, то задается положение точки относительно предыдущей, то есть используются относительные прямоугольные координаты. В трехмерных чертежах чаще применяют именно относительные координаты.

Цилиндрические координаты

Абсолютные цилиндрические координаты представляются в формате расстояние<угол,расстояние. В данной записи первое расстояние – это длина проекции на плоскость XY вектора, начинающегося в начале текущей системы и заканчивающегося в точке, координаты которой задаются. Угол указывает значение между осью X и упомянутой проекцией вектора на плоскость XY. Второе расстояние, которое вводится после запятой, – это смещение точки вдоль оси Z. Как видно, цилиндрические координаты отличаются от полярных лишь добавлением координаты z Как задается точка с координатами 10<30,5 показано на рис. 9.13.

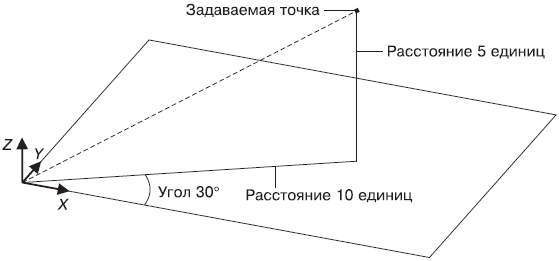
Рис. 9.13. Указание точки методом абсолютных цилиндрических координат

Если применяются относительные цилиндрические координаты, то перед предыдущей записью будет еще добавлен символ @. Тогда координата точки будет указываться путем смещения ее относительно предыдущей. Следует заметить, что при использовании цилиндрических координат, как абсолютных, так и относительных, указываемые расстояния фактически представляют собой катеты прямоугольного треугольника.

Сферические координаты

Абсолютные сферические координаты представляются в формате расстояние <угол <угол. В данной записи расстояние – это длина вектора, который проходит от начала координат до указываемой точки. Первый угол отсчитывается от оси X до проекции вектора на плоскость XY. Еще одно значение, которое следует указать, – это угол между плоскостью XY и упомянутым вектором. Точка с координатами 5<30<45 показана на рис. 9.14.

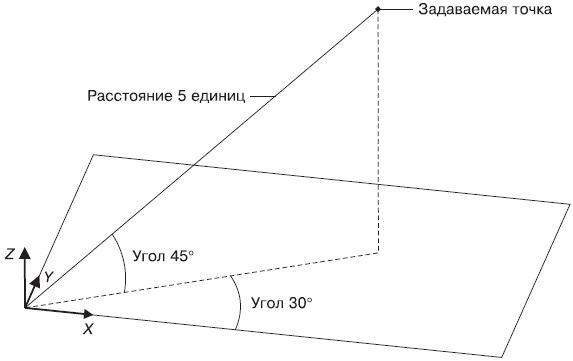
Рис. 9.14. Указание точки методом абсолютных сферических координат

Сферические координаты также могут быть и относительными. В этом случае как всегда добавляется знак @, а координата точки указывается путем смещения ее от предыдущей точки. Следует отметить, что, в отличие от цилиндрических координат, где расстояние до точки указывалось косвенным образом, в сферических координатах расстояние до точки указывается прямо.

Данный текст является ознакомительным фрагментом.