Сложение гармоник и разложение на гармонические составляющие

Сложение гармоник и разложение на гармонические составляющие

Создадим новый входной файл, соответствующий рис. 7.4, на котором к схеме рис. 7.1 добавлены еще два независимых источника тока. 

Мы использовали два источника только для того, чтобы вы могли получить основную и вторую гармоники на одном графике с выходным напряжением. Дополнительные источники питают подключенный параллельно 1-омный резистор. Такое изменение первоначальной схемы совсем не обязательно, просто оно оказалось удобным при данном наборе параметров. Новый входной файл представляет собой расширение предыдущего файла и выглядит следующим образом:

Fourier Analysis; Decomposition of Polynomial

Vin 1 0 sin(0 1 1000);аргументы - смещение, амплитуда и частота

Rin 1 0 1MEG

Е 2 0 poly(1) 1,0 1 1 1; последние 3 записи for k0, k1, k2

Rout 2 0 1MEG

i1 0 3 sin(1 1 1000)

i2 0 3 sin(0.5 0.5 2000 0 0 -90)

r 3 0 1

.TRAN 1us 1ms

.FOUR 1000 V(1) V(2) V(3)

.PROBE

.END

Рис. 7.4. Схема для анализа сложения гармоник и разложения в ряд Фурье 

Перед выполнением анализа подробно рассмотрим описания для i₁ и i₂. Для гармонического синтеза используются результаты разложения в ряд Фурье из предыдущей задачи. Убедитесь, что вы понимаете смысл всех параметров; затем выполните анализ в Probe, получив графики I(i1), I(i2) и I(r). Хотя они и представляют собой токи, но численно они равны напряжениям, так как проходят через сопротивление в 1 Ом. На рис. 7.5 представлены результаты. Теперь можно установить, что первый график представляет собой основную гармонику, второй — вторую гармонику, а третий — результат сложения их в резисторе r. Конечно, можно получить график V(3) вместо I(r). При этом ось Y будет размечена в единицах напряжения, а не тока. Убедитесь, что сумма двух первых кривых дает третью кривую в различные моменты времени. Чтобы сделать график более компактным, мы использовали смещение в 1 В для основной гармоники и в 0,5 В — для второй гармоники. Фактически основная гармоника имеет нулевое смещение.

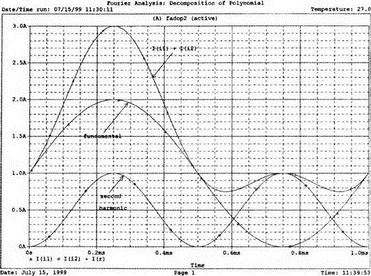
Рис. 7.5. Основная и вторая гармоники и результат их сложения