Глава 13 А как насчет вычитания?
Убедившись в том, что реле действительно можно соединить для сложения двоичных чисел, зададимся вопросом: «А как насчет вычитания?» Не бойтесь показаться смешным, задавая его. На самом деле вы довольно проницательны. Сложение и вычитание в некотором смысле дополняют друг друга, однако механика у этих операций разная. Сложение предполагает последовательное продвижение от крайнего правого столбца цифр до крайнего левого. Каждое значение, перенесенное из одного столбца, прибавляется к следующему. При вычитании мы ничего не переносим; мы заимствуем, а это действие предполагает использование довольно запутанного механизма.
Давайте рассмотрим типичную задачу на вычитание с заимствованием.

Начнем решение с крайнего правого столбца. Сначала мы замечаем, что 6 больше 3, поэтому нам нужно занять 1 у 5, а затем вычесть 6 из 13, в результате чего получается 7. Мы помним, что заняли 1 у 5, поэтому вместо 5 имеем 4, что меньше 7, поэтому занимаем 1 у 2, вычитаем 7 из 14 и получаем 7. Мы заняли 1 у 2, поэтому у нас есть только единица, из которой вычитаем 1 и получаем 0. Наш ответ — 77.
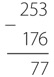
Как же заставить группу логических вентилей следовать такой странной логике?
Не будем даже пытаться. Вместо этого используем небольшой трюк, позволяющий вычитать без заимствования. Это порадовало бы Полония («Не занимай и не ссужай») и всех остальных. Кроме того, подробное рассмотрение процесса вычитания полезно, поскольку напрямую связано с использованием двоичных кодов для хранения в компьютерах отрицательных чисел.
Числа, участвующие в операции вычитания, называются уменьшаемым и вычитаемым. Вычитаемое вычитается из уменьшаемого, результатом является разность.

Чтобы произвести вычитание без заимствования, сначала нужно вычесть вычитаемое из 999, а не из уменьшаемого.
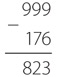
В данном случае используем число 999, поскольку числа, участвующие в операции, состоят из трех цифр. Если бы они были четырехзначными, мы бы использовали число 9999. При вычитании числа из строки девяток получаем число, называемое дополнением до девяти. Дополнение числа 176 до девяти — 823. Это работает и в обратную сторону: дополнение числа 823 до девяти — 176. Вся прелесть в том, что вне зависимости от значения вычитаемого вычисление его дополнения до девяти никогда не требует заимствования.
После вычисления дополнения вычитаемого до девяти нужно прибавить к нему исходное уменьшаемое.
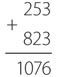
Наконец, прибавить 1 и вычесть 1000.

Вот и всё. Мы получили такой же результат, как и раньше, ни разу не прибегнув к заимствованию.
Почему это работает? Исходная задача на вычитание такова:
253 – 176.
Если к этому выражению прибавить и вычесть любое число, результат останется прежним. Так что давайте прибавим и вычтем 1000:
253 – 176 + 1000 – 1000.
Выражение эквивалентно следующему:
253 – 176 + 999 + 1 – 1000.
Теперь числа можно перегруппировать:
253 + (999 – 176) + 1 – 1000.
Это соответствует вычислению, которое я продемонстрировал с использованием дополнения до девяти. Мы заменили одно вычитание двумя вычитаниями и двумя сложениями, избавившись при этом от всех нежелательных заимствований.
А если вычитаемое больше уменьшаемого? Рассмотрим такой пример.

Обычно вы смотрите на подобную задачу и думаете: «Хм, вычитаемое больше уменьшаемого, поэтому придется поменять числа местами, выполнить вычитание и не забыть о том, что результат будет отрицательным». Вы можете произвести перестановку чисел в голове и записать ответ следующим образом.
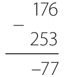
Процесс выполнения данного расчета без заимствований несколько отличается от предыдущего примера. Как и раньше, мы начинаем с вычитания вычитаемого (253) из 999 для получения дополнения до девяти.
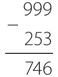
Теперь прибавим дополнение до девяти к исходному уменьшаемому.

На этом этапе в более раннем примере для получения окончательного результата мы могли прибавить 1 и вычесть 1000. Однако в данном случае эта стратегия не сработала бы, поскольку нам пришлось бы вычесть 1000 из 923, что в действительности потребовало бы вычесть 923 из 1000, и без заимствований мы бы не обошлись.
Вместо этого, по аналогии с прибавлением 999, вычтем 999.

Сразу становится очевидным, что наш ответ будет отрицательным, поэтому следует поменять числа местами и вычесть 922 из 999. Это опять же не требует заимствований, а ответ совпадает с ожидаемым.

Этот метод применим и к двоичным числам, работать с которыми оказывается проще, чем с десятичными. Давайте посмотрим, как это работает.
Вот исходная задача на вычитание.
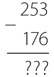
После преобразования чисел в двоичные получаем следующую задачу.
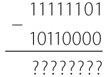
Шаг 1. Вычесть вычитаемое из 11111111 (что соответствует 255).
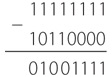
При работе с десятичными числами вычитаемое вычиталось из строки девяток, а результат назывался дополнением до девяти. При работе с двоичными числами вычитаемое вычитается из строки единиц, результат — дополнение до единицы. Заметьте, что нам на самом деле не нужно выполнять вычитание, чтобы вычислить дополнение до единицы, поскольку каждый 0 в исходном числе превращается в 1 в дополнении до единицы, а каждая 1 превращается в 0. По этой причине дополнение до единицы иногда также называется отрицанием или инверсией. (Сейчас вы, вероятно, вспомнили о том, что в главе 11 мы конструировали устройство, называемое инвертором, которое меняло 0 на 1, а 1 на 0.)
Шаг 2. Прибавить дополнение вычитаемого до единицы к уменьшаемому.

Шаг 3. Прибавить к результату 1.
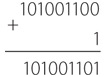
Шаг 4. Вычесть 100000000 (что соответствует 256).

Результат эквивалентен десятичному числу 77.
Давайте попробуем еще раз, поменяв числа местами. В десятичной системе счисления задача на вычитание выглядит так.
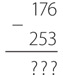
В двоичной системе — так.

Шаг 1. Вычесть вычитаемое из 11111111, чтобы получить дополнение до единицы.

Шаг 2. Прибавить дополнение вычитаемого до единицы к уменьшаемому.

Теперь нужно как-то вычесть из результата число 11111111. Когда исходное вычитаемое меньше уменьшаемого, для этого достаточно прибавить 1 и вычесть 100000000. Однако эту операцию нельзя выполнить без заимствования. Вместо этого мы вычитаем результат из числа 11111111.
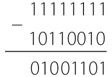
Опять же, такая стратегия на самом деле означает, что для получения результата мы выполняем простое инвертирование. Ответ снова равен 77, а на самом деле ?77.
Теперь у нас есть необходимые знания для оснащения собранного в предыдущей главе сумматора функцией вычитания. Чтобы не слишком усложнять эту счетную машину, сделаем так, чтобы она выполняла вычитание только тогда, когда вычитаемое меньше уменьшаемого, когда в результате получается положительное число.
Основой этой счетной машины являлся 8-разрядный сумматор, собранный из логических вентилей.
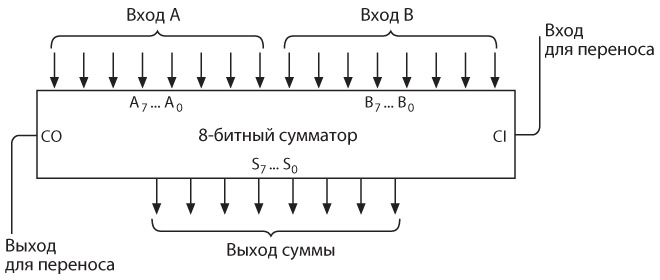
Вероятно, вы помните, что входы с A0 по A7 и с B0 по B7 были подключены к переключателям, с помощью которых вводились два 8-битных числа, подлежащие сложению. Вход для переноса соединялся с землей, выходы с S0 по S7 — с восемью лампочками, отображающими результат сложения. Поскольку в итоге могло получиться 9-битное значение, выход для переноса был подключен к девятой лампочке.
Пульт управления выглядел так.

Положения переключателей на этом изображении соответствуют сложению чисел 183 (10110111) и 22 (00010110), в результате которого получается 205, или 11001101, что и отражено рядом лампочек.
Новый пульт управления для сложения и вычитания двух 8-битных чисел имеет несколько иной вид. Он предусматривает дополнительный переключатель, позволяющий выбрать между сложением и вычитанием.
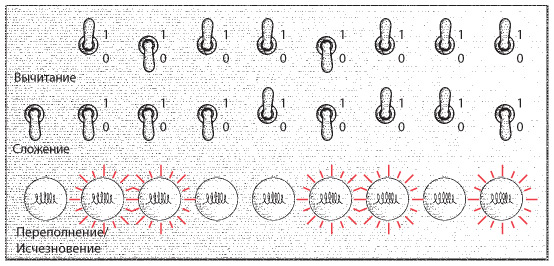
Подписи подсказывают, что размыкание этого переключателя соответствует сложению, а замыкание — вычитанию. Кроме того, для отображения результатов используются только восемь крайних лампочек справа. Девятая лампочка обозначена словами «Переполнение/Исчезновение». Она загорается, когда полученное число не может быть представлено восемью лампочками. Так происходит, если в результате сложения получается число, превышающее 255 (это называется переполнением), или если результат вычитания — отрицательное число — исчезновение порядка, то есть если вычитаемое больше уменьшаемого.
Главное нововведение в счетной машине — схема, которая вычисляет дополнение до единицы для 8-битного числа. Напомним, что вычисление дополнения до единицы эквивалентно инвертированию битов, поэтому устройство для произведения этой операции могло бы состоять просто из восьми инверторов.
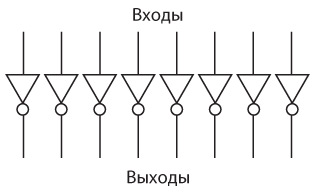
Проблема этой схемы заключается в том, что она всегда инвертирует поступающие в нее биты. Наша цель — создать машину, которая выполняет как сложение, так и вычитание, поэтому эта схема должна инвертировать биты только при выполнении вычитания. Вот более подходящая схема.
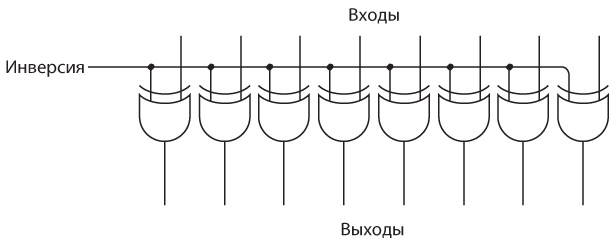
Сигнал «Инверсия» поступает на каждый из восьми вентилей Искл-ИЛИ (исключающее ИЛИ). Напомним, вентиль Искл-ИЛИ работает так.
Если сигнал «Инверсия» равен 0, то сигналы на восьми выходах вентилей Искл-ИЛИ совпадают с сигналами на их входах. Например, если на вход подается значение 01100001, то выходным значением также является 01100001. Если сигнал «Инверсия» равен 1, то восемь входных сигналов будут инвертированы. Если на вход подается значение 01100001, то выходное — 10011110.
Давайте поместим эти восемь вентилей Искл-ИЛИ в прямоугольник под названием «Дополнение до единицы».
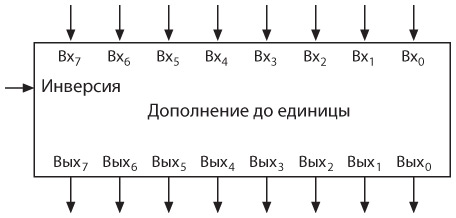
Теперь устройство для дополнения числа до единицы, 8-битный сумматор и последний вентиль Искл-ИЛИ можно объединить в схему.
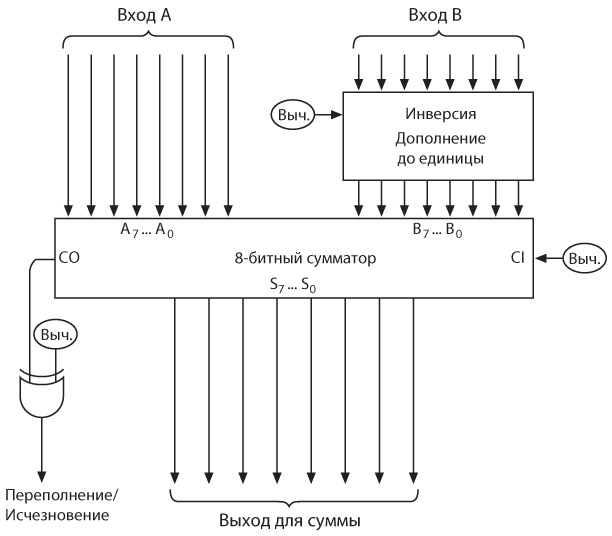
Обратите внимание на три сигнала, обозначенные как «Выч.». Они поступают от переключателя «Сложение/вычитание». Этот сигнал равен 0, если необходимо выполнить сложение, и 1, если вычитание. При вычитании сигналы на входах B (второй ряд переключателей) инвертируются схемой «Дополнение до единицы» перед попаданием в сумматор. Кроме того, при вычитании к результату сложения прибавляется 1 за счет подачи на вход сумматора CI (вход для переноса) значения 1. При сложении схема «Дополнение до единицы» не оказывает никакого эффекта, а вход CI равен 0.
Сигнал «Выч.» и выходной сигнал сумматора CO (выход для переноса) также подаются на вход вентиля Искл-ИЛИ, который используется для включения лампочки «Переполнение/Исчезновение». Если сигнал «Выч.» равен 0 (выполняется сложение), лампочка будет гореть при выходном сигнале сумматора CO, равном 1. Это означает, что результат сложения превышает 255.
При выполнении вычитания, когда вычитаемое (переключатели B) меньше уменьшаемого (переключатели A), выходной сигнал сумматора CO бывает равен 1. Это нормально и означает, что на последнем этапе необходимо вычесть 100000000. Таким образом, лампа «Переполнение/Исчезновение» горит только тогда, когда выход сумматора CO равен 0, то есть вычитаемое больше уменьшаемого и результат отрицательный. Описанная выше машина не предназначена для отображения отрицательных чисел.
Сейчас вы, вероятно, рады, что спросили: «А как насчет вычитания?»
В этой главе я говорил об отрицательных числах, но все еще не показал, как выглядят отрицательные двоичные числа. Вы можете предположить, что традиционный знак «–» используется с двоичными числами так же, как и с десятичными. Например, число –77 в двоичном формате записывается –1001101. Конечно, вы можете так его записать, однако одна из целей использования двоичных чисел заключается в том, чтобы представлять всё с помощью нулей и единиц, включая такие символы, как «–» перед отрицательным числом.
Можно просто использовать еще один бит для знака «–». Его значение 1 может соответствовать отрицательному числу, а 0 — положительному, и это будет работать, хотя мало что даст. Существует еще одно решение для представления отрицательных чисел, которое также предусматривает простой способ сложения отрицательных и положительных чисел. Недостаток этого метода — необходимость заранее решить, сколько цифр требуется для представления чисел, с которыми мы будем работать.
Давайте подумаем. Преимущество обычного способа представления положительных и отрицательных чисел заключается в том, что они могут иметь бесконечную длину. Мы представляем 0 как точку, от которой в одну сторону в бесконечность уходят положительные числа, а в другую — отрицательные.
… –1 000 000 –999 999 … –3 –2 –1 0 1 2 3 … 999 999 1 000 000 …
Однако представьте, что нам не нужно бесконечное количество чисел: с самого начала известно, что каждое число, которое встретится, будет находиться в определенном диапазоне.
Рассмотрим чековый банковский счет, в котором мы иногда сталкиваемся с отрицательными числами. Предположим, что баланс нашего счета никогда не превышал 500 долларов, и банк установил лимит перерасхода на те же 500 долларов. Это значит, что баланс нашего счета всегда находится в диапазоне от 499 до –500 долларов. При этом мы никогда не кладем на счет более 499 долларов, никогда не выписываем чек на сумму более 500 долларов и имеем дело только с долларами, центы же не учитываем.
Этот набор условий указывает, что при использовании нашего счета мы имеем дело с числами в диапазоне от –500 до 499. Это всего 1000 чисел. Такое ограничение подразумевает, что для представления всех нужных чисел мы должны использовать только три десятичные цифры и обходиться без знака «–». Хитрость в том, что нам не нужны положительные числа от 500 до 999, поскольку мы уже решили, что максимальным положительным числом для нас является 499. Таким образом, трехзначные числа от 500 до 999 фактически можно использовать для представления отрицательных чисел. Вот как это работает.
Вместо –500 используем 500.
Вместо –499 используем 501.
Вместо –498 используем 502.
…
Вместо –2 используем 998.
Вместо –1 используем 999.
Вместо 0 используем 000.
Вместо 1 используем 001.
Вместо 2 используем 002.
…
Вместо 497 используем 497.
Вместо 498 используем 498.
Вместо 499 используем 499.
Другими словами, каждое трехзначное число, которое начинается с цифры 5, 6, 7, 8 или 9, фактически является отрицательным. Вместо того чтобы записывать эти числа как:
–500 –499 –498 … –4 –3 –2 –1 0 1 2 3 4 … 497 498 499,
запишем их:
500 501 502 … 996 997 998 999 000 001 002 003 004 … 497 498 499.
Обратите внимание: числа идут по кругу. Наименьшее отрицательное число (500) как бы следует за наибольшим положительным числом (499). А число 999 (которое фактически равно –1) на единицу меньше нуля. Если мы прибавим 1 к 999, то в обычных условиях получим 1000. Но поскольку мы имеем дело только с тремя цифрами, в результате будет 000.
Такой способ записи отрицательных чисел называется дополнением до десяти. Чтобы преобразовать трехзначное отрицательное число в дополнение до десяти, вычитаем его из 999 и прибавляем 1. Другими словами, дополнение до десяти — это дополнение до девяти плюс один. Например, чтобы найти дополнение числа –255 до десяти, нужно вычесть его из 999, получив 744, а затем прибавить 1, что в результате даст 745.
Вероятно, вы слышали утверждение, что вычитание — это просто прибавление отрицательных чисел. На что вы, вероятно, отвечали: «Да, но числа все равно приходится вычитать». Используя дополнение до десяти, вы вообще ничего не вычитаете. Все сводится к сложению.
Предположим, у вас на счету 143 доллара. Вы выписываете чек на 78 долларов. Это означает, что вы должны прибавить –78 к 143. Дополнение числа –78 до десяти равно 999 – 078 + 1, то есть 922. Таким образом, ваш баланс теперь составляет 143 + 922, или 65 долларов (без учета переполнения). Если после этого вы выпишете чек на 150 долларов, придется прибавить число –150, дополнение которого до десяти равно 850. Итак, прибавим 850 к предыдущему балансу 065 и получим 915 — новый баланс. Это число фактически эквивалентно –85.
В двоичном формате подобная система называется дополнением до двух. Предположим, что мы работаем с 8-битными числами в диапазоне от 00000000 до 11111111, которые соответствуют десятичным числам от 0 до 255. Если вам требуется использовать отрицательные числа, то каждое 8-битное число, начинающееся с 1, фактически будет отрицательным:
Двоичное число
Десятичное число
10000000
–128
10000001
–127
10000010
–126
10000011
–125
…
…
11111101
–3
11111110
–2
11111111
–1
00000000
0
00000001
1
00000010
2
…
…
01111100
124
01111101
125
01111110
126
01111111
127
Теперь вы можете представить числа в диапазоне от –128 до +127. Старший значащий бит (крайний слева) называется знаковым разрядом. Знаковый разряд равен 1 для отрицательных чисел и 0 — для положительных.
Чтобы вычислить дополнение числа до двух, сначала вычислите его дополнение до единицы, а затем прибавьте 1. Это эквивалентно инвертированию всех цифр и прибавлению 1. Например, десятичное число 125 в двоичном формате выражается как 01111101. Чтобы выразить число –125 в виде дополнения до двух, сначала инвертируем цифры 01111101 для получения 10000010, а затем прибавим 1, в результате чего получим 10000011. Вы можете проверить результат по приведенной выше таблице. Для выполнения обратной операции повторите те же действия — инвертируйте все биты и прибавьте 1.
Эта система позволяет выражать положительные и отрицательные числа, не используя знак «–». Кроме того, с ее помощью можно складывать положительные и отрицательные числа, руководствуясь только правилами сложения. Например, сложим двоичные эквиваленты чисел –127 и 124. Это просто, если использовать в качестве шпаргалки предыдущую таблицу.
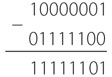
Результат эквивалентен числу –3 в десятичной системе счисления.
В данном случае нужно следить за условиями переполнения и исчезновения разряда. Такое может произойти, когда в результате сложения получается число больше 127 или меньше –128. Например, вы прибавляете 125 к 125.

Поскольку старший бит равен 1, результат следует интерпретировать в качестве отрицательного числа, которое соответствует –6 в десятичной системе счисления. Что-то подобное происходит и при сложении чисел –125 и –125.
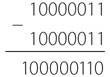
С самого начала мы решили ограничиться 8-битными числами, поэтому необходимо проигнорировать крайнюю левую цифру. Правые восемь бит эквивалентны числу +6.
Вообще, результат сложения положительных и отрицательных чисел не является верным, если знаковые разряды двух операндов одинаковы, а знаковый разряд результата отличается.
Теперь у нас есть два разных способа использования двоичных чисел. Двоичное число может быть со знаком (знаковым) или без знака (беззнаковым). Восьмибитные числа без знака находятся в диапазоне от 0 до 255, 8-битные числа со знаком — в диапазоне от ?128 до 127. По самим числам невозможно понять, сопровождаются они знаком или нет. Например, кто-то говорит: «У меня есть 8-битное двоичное число, значение которого равно 10110110. Каков его десятичный эквивалент?» Сначала вы должны спросить: «Это число со знаком или без знака? В зависимости от этого ответом может быть либо число –74, либо 182».
В этом и состоит проблема с битами: они всего лишь нули и единицы, которые ничего не говорят о себе.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК