Пальчиковые игры и математика
Пальчиковые игры и математика
Дети используют пальцы для счета еще до того, как начинают размышлять о цифрах. Счет на пальцах был обычным делом уже в Древнем Египте. Практически во всех культурах дети учатся считать при помощи пальцев: они всегда перед глазами и доступны, и их всегда можно сравнить с количеством предметов, которые надо посчитать. Все умеют это делать. До пяти можно сосчитать на одной руке. Начиная с числа «шесть» понадобятся обе руки; используя их, для осязания и моторики вводят в действие оба полушария головного мозга. Поэтому должен существовать обмен информацией между обоими полушариями головного мозга, а для этого обмена требуется время. И поскольку использование головного мозга изменяет его и именно благодаря этому в конечном итоге в нашем головном мозге формируются отвлеченные числа, можно исходить из того, что числа от шести до десяти откладываются в обоих полушариях головного мозга, тогда как для чисел от одного до пяти достаточно одного полушария.
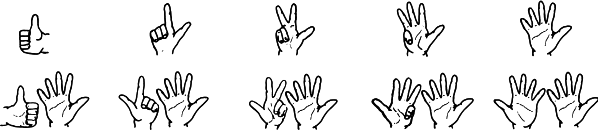
7.6. Счет на пальцах
Китайцы действуют иначе (см. рис. ниже). Они используют комбинации и определенные положения пальцев — так они могут считать до десяти на пальцах одной руки. Лишь начиная с одиннадцати им нужна вторая рука. Тем самым они подключают оба полушария головного мозга только с числа «одиннадцать». Можно, конечно, предположить, что для абстрактного применения цифр в арифметике это не имеет никакого значения, особенно если учесть, что взрослые не используют пальцы для решения простых арифметических задач в пределах от одного до двадцати. Для этого пальцы никому не нужны.
То, что числа в нашем головном мозге представлены не только в образе наших пальцев, показывает один очень простой эксперимент. Закройте глаза и представьте себе числа от одного до девяти на одной линии. Как выглядит ваша мысленная картина? Большинство людей говорит, что они представляют себе горизонтальную линию, с единицей слева, за которой идет двойка и так далее до девятки на правой стороне. Следовательно, мы представляем себе числовой луч в пространстве. Поскольку мы обычно представляем себе меньшие числа на левой стороне, а большие — на правой и поскольку правое полушарие головного мозга отвечает за левую сторону, а левое полушарие головного мозга — за правую, то с помощью соответствующих экспериментов можно найти доказательства существования такого числового луча в нашей голове.
7.7. Китайцы умеют считать до десяти на пальцах только одной руки.
Самое простое задание заключалось в следующем: испытуемых попросили представить себе сначала одно число (эталонное), а затем второе число, которое может быть больше или меньше эталонного. Затем испытуемые должны были указательным пальцем правой или левой руки указать на отличную от эталонной цифру. Оказалось, что испытуемые, как правило, быстрее указывали левой рукой, если число было меньше эталонного, а правой — если оно было больше эталонного. Притом весь процесс не зависел от какого-либо конкретного числа: не все числа меньше какого-то определенного числа помещены в правом полушарии головного мозга, и не все числа, превышающие его, — в левом полушарии. Одно и то же число может быть представлено слева или справа — это зависит от того, какое эталонное число было предъявлено сначала (то есть где именно на числовом луче мы мысленно находимся в данный момент). Мы можем мысленно двигаться вдоль числового луча, а эталонное число может находиться посередине, при этом бо?льшие числа будут помещаться на правой стороне нашего мысленного пространства, а меньшие — на левой. Эффект обнаруживается даже тогда, когда испытуемым показывают числа не в виде цифр, а в виде слов — числительных.
Можно было бы полагать, что результат эксперимента — простое воздействие факта, что за левую сторону нашего организма отвечает правое полушарие головного мозга, и наоборот. Однако это не так: эффект наступает и тогда, когда задействуется только одна рука: «меньше» перерабатывается слева, а «больше» — справа. Итак, числовой луч скорее связан с пространством вокруг нас, нежели с нашими пальцами или нашим телом. Он — другое, более абстрактное представление о числе, нежели «считающие» пальцы. И развивается это абстрактное представление позже, потому что теменная доля (место числового луча в нашем головном мозге) развивается намного позднее, чем простые сенсорные и моторные участки, которые играют роль при счете на пальцах.
Итак, числа перерабатываются головным мозгом по-разному: (1) как сенсорное и моторное событие, тесно связанное с пальцами, (2) как место на числовом луче в нашем теменном мозге и (3) как слово в речевых центрах. Теперь мы сочли бы, что при обращении с числами (в зависимости от того, о каком именно числе идет речь), используется один из этих модулей головного мозга. В принципе это так, однако эти модули с начала изучения чисел находятся в тесном контакте, так что активизированы будут все.
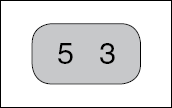
7.8. Какое число больше? Под экраном находятся две кнопки, и участники эксперимента должны нажать клавишу на стороне бо?льшего числа, которое может находиться слева или справа. Использовались только пары чисел, различающихся на два, от «1 3» или «3 1» до «18 20» до «20 18». Каждый испытуемый выполнял 432 таких заданий, и время, необходимое для выполнения каждого отдельного задания, измерялось в миллисекундах.
На основе этого главного вывода был проведен еще один эксперимент, очень необычный. Немецкие и китайские испытуемые обоих полов в возрасте примерно 25 лет должны были выполнить на компьютере простое задание — сравнить числа. Время, которое понадобилось им, чтобы указать, какое из двух чисел больше, измерялось в миллисекундах. Сравнительное исследование проводилось на немцах и китайцах, потому что в этих культурах счету на пальцах учатся по-разному; немцы используют пальцы второй руки для чисел, начиная с шести, китайцы же — только начиная с одиннадцати. Передача данных от одного полушария головного мозга в другое требует времени, — идея эксперимента заключалась в том, чтобы измерить это время у взрослых.
Три вещи, касающиеся результатов, были известны заранее:
(1) Задания на сравнение чисел тем труднее (и требует больше времени), чем больше числа. Мы действительно сравниваем «2 4» быстрее, чем «12 14».
(2) Задание на сравнение чисел является особенно легким (а время реакции — меньшим) тогда, когда на одной стороне сравнения стоит одноразрядное, а на другой — двухразрядное число: «Что больше: X или XX?» Ответить на этот вопрос можно, вовсе не раздумывая об этих числах, то есть не распознавая и не классифицируя их (светло-серые участки на графике ниже).
(3) Китайцы почти все время в начальной школе проводят за изучением нескольких тысяч иероглифов, составляющих их письменность. Они с детства натренированы распознавать символы — в отличие от немецких школьников, которые за год запоминают примерно тридцать букв алфавита и дальше занимается совсем другими вещами. Поэтому не удивительно, что и числа китайцы различают быстрее, чем немцы.
Эти три эффекта четко заметны, если рассмотреть фактические результаты исследования. Для бо?льших чисел время реакции было больше; сравнения пар типа «8 10» и «9 11» проходили явно быстрее; китайцы в целом были быстрее, чем немцы. Немецкие испытуемые были к тому же медленнее при сравнении чисел, начиная с шести, то есть как только следовало переработать число больше пяти. Китайские испытуемые проявили соответствующее замедление только при сравнении «10 12» (когда в действие вступала «вторая рука»).
Результаты показали, таким образом, некую «тень» детского счета на пальцах, сопутствующую счету во взрослом возрасте. Разумеется, испытуемые решали задания на сравнение не на пальцах, однако значения времени реакции показывают, что формирование головного мозга в детском саду ни в коем случае не прошло бесследно для его функционирования в дальнейшей жизни. Уже почти сто лет нам известно, что пальцы и математика в нашей голове очень тесно связаны друг с другом: при любой математической операции наши пальцы, если можно так выразиться, снова в игре. Абстрактные числа, величины и т. п. когда-то надо было потрогать пальцами, ведь лишь так они попадают в головной мозг. Именно поэтому даже такой сложный умственный труд — математика — в большой степени имеет дело с нашим «пространственным» телом и особенно с нашими пальцами.
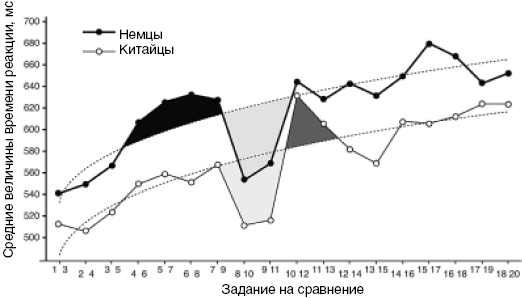
7.9. Средние величины времени реакции при выполнении задания на сравнение чисел у китайских и немецких испытуемых. Пунктирные кривые даны для того, чтобы сделать более наглядными отклонения величин.
Другими словами: то, насколько хорошо мы умеем обращаться с нашими пальцами, насколько активно мы в детстве пользовались ими, имеет значение для способности обращаться с числами. Если вы действительно хотите, чтобы как можно больше детей, находящихся сейчас в детсадовском возрасте, позднее стали превосходными специалистами в области математики и информатики, то чему следовало бы отдать предпочтение в детском саду: ноутбукам или пальчиковым играм? Ответ науки ясен: пальчиковым играм!
Данный текст является ознакомительным фрагментом.