Последовательные подсостояния
Последовательные подсостояния
Последовательные подсостояния (sequential substates) используются для моделирования такого поведения объекта, во время которого в каждый момент времени объект может находиться в одном и только одном подсостояний. Поведение объекта в этом случае представляет собой последовательную смену подсостояний, начиная от начального и заканчивая конечным подсостояниями. Хотя объект продолжает находиться в составном состоянии, введение в рассмотрение последовательных подсостояний позволяет учесть более тонкие логические аспекты его внутреннего поведения.
Для примера рассмотрим в качестве моделируемого объекта обычный телефонный аппарат. Он может находиться в различных состояниях, одним из которых является состояние дозвона до абонента. Очевидно, для того чтобы позвонить, необходимо снять телефонную трубку, услышать тоновый сигнал, после чего набрать нужный телефонный номер. Таким образом, состояние дозвона до абонента является составным и состоит из двух последовательных подсостояний: «поднять телефонную трубку» и «набрать телефонный номер». Фрагмент диаграммы состояний для этого примера содержит одно составное состояние и два последовательных подсостояний (рис. 6.7).
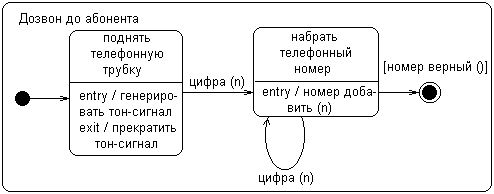
Рис. 6.7. Пример составного состояния с двумя вложенными последовательными подсостояниями
Некоторых пояснений могут потребовать переходы. Два из них специфицируют событие-триггер набор цифры, которое имеет имя «цифра» с параметром "п". В качестве параметра, как нетрудно предположить, выступает отдельная цифра на диске телефонного аппарата. Переход из начального под-состояния нетриггерный, поскольку он не содержит никакой строки текста. Последний переход в конечное подсостояние не имеет события-триггера, но имеет сторожевое условие, проверяющее правильность набранного номера абонента. Только в случае истинности этого условия телефонный аппарат может перейти в конечное подсостояние, которое характеризует суперсостояние «дозвон до абонента» в целом.
Составное состояние может содержать в качестве вложенных подсостояний начальное и конечное состояния. При этом начальное подсостояние является исходным, когда происходит переход объекта в данное составное состояние. Если составное состояние содержит внутри себя конечное подсостояние, то переход в это вложенное конечное состояние означает завершение нахождения объекта в данном вложенном состоянии. Важно помнить, что для последовательных подсостояний начальное и конечное состояния должны быть единственными в каждом составном состоянии.
Это можно объяснить следующим образом. Каждая совокупность вложенных последовательных подсостояний представляет собой подавтомат того автомата, которому принадлежит рассматриваемое составное состояние. Поскольку каждый автомат может иметь по определению единственное начальное и единственное конечное состояния, то для подавтомата это условие также должно выполняться (рис. 6.7).
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Параллельные подсостояния
Параллельные подсостояния Параллельные подсостояния (concurrent substates) позволяют специфицировать два и более подавтомата, которые могут выполняться параллельно внутри составного события. Каждый из подавтоматов занимает некоторую область (регион) внутри составного
Последовательные цепи на постоянном токе
Последовательные цепи на постоянном токе Простая схема постоянного тока, состоящая из источника напряжения и трёх резисторов, могла бы быть описана в уже знакомом нам листинге:Series Circuit with Source and Three ResistorsV1 1 0 2 4VR1 1 2 50R2 2 3 100R3 3 0 80В PSpice это был бы листинг входного или схемного
4.9. Последовательные и параллельные серверы
4.9. Последовательные и параллельные серверы Сервер в нашем простом примере из предыдущего раздела являлся последовательным сервером (iterative server). Он последовательно обрабатывал запросы клиентов, переходя к следующему только после полного завершения работы с предыдущим.
Последовательные итераторы (Forward iterators)
Последовательные итераторы (Forward iterators) Класс или встроенный тип X удовлетворяет требованиям последовательного итератора, если справедливы следующие выражения:Таблица 4. Требования последовательного итератора выражение возвращаемый тип семантика исполнения
7.3.4. Последовательные порты
7.3.4. Последовательные порты Файл /proc/tty/driver/serial содержит конфигурационную и статистическую информацию о последовательных портах. Эти порты нумеруются начиная с нуля.[24] Работать с настройками порта позволяет также команда setserial, но файл /proc/tty/driver/serial, помимо всего прочего,