6.1. Автоматы

6.1. Автоматы

Автомат (state machine) в языке UML представляет собой некоторый формализм для моделирования поведения элементов модели и системы в целом. В метамодели UML автомат является пакетом, в котором определено множество понятий, необходимых для представления поведения моделируемой сущности в виде дискретного пространства с конечным числом состояний и переходов. С другой стороны, автомат описывает поведение отдельного объекта в форме последовательности состояний, которые охватывают все этапы его жизненного цикла, начиная от создания объекта и заканчивая его уничтожением. Каждая диаграмма состояний представляет некоторый автомат.

Простейшим примером визуального представления состояний и переходов на основе формализма автоматов может служить рассмотренная выше ситуация с исправностью технического устройства, такого как компьютер. В этом случае вводятся в рассмотрение два самых общих состояния: «исправен» и «неисправен» и два перехода: «выход из строя» и «ремонт». Графически эта информация может быть представлена в виде изображенной ниже диаграммы состояний компьютера (рис. 6.1).

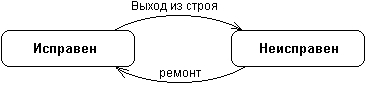
Рис. 6.1. Простейший пример диаграммы состояний для технического устройства типа компьютер

Основными понятиями, входящими в формализм автомата, являются состояние и переход. Главное различие между ними заключается в том, что длительность нахождения системы в отдельном состоянии существенно превышает время, которое затрачивается на переход из одного состояния в другое. Предполагается, что в пределе время перехода из одного состояния в другое равно нулю (если дополнительно ничего не сказано). Другими словами, переход объекта из состояния в состояние происходит мгновенно.

В общем случае автомат представляет динамические аспекты моделируемой системы в виде ориентированного графа, вершины которого соответствуют состояниям, а дуги – переходам. При этом поведение моделируется как последовательное перемещение по графу состояний от вершины к вершине по связывающим их дугам с учетом их ориентации. Для графа состояний системы можно ввести в рассмотрение специальные свойства.

Одним из таких свойств является выделение из всей совокупности состояний двух специальных: начального и конечного. Хотя ни в графе состояний, ни на диаграмме состояний время нахождения системы в том или ином состоянии явно не учитывается, предполагается, что последовательность изменения состояний упорядочена во времени. Другими словами, каждое последующее состояние всегда наступает позже предшествующего ему состояния.

Еще одним свойством графа состояний может служить достижимость состояний. Речь идет о том, что навигация или ориентированный путь в графе состояний определяет специальное бинарное отношение на множестве всех состояний системы. Это отношение характеризует потенциальную возможность перехода системы из рассматриваемого состояния в некоторое другое состояние. Очевидно, для достижимости состояний необходимо наличие связывающего их ориентированного пути в графе состояний.

Формализм автоматов допускает вложение одних автоматов в другие для уточнения внутренней структуры отдельных более общих состояний (макросостояний). В этом случае вложенные автоматы получили название подавтоматов. Подавтоматы могут использоваться для внутренней спецификации процедур и функций, образующих поведение исходного объекта. Например, состояние неисправности технического устройства (рис. 6.1) может быть детализировано на отдельные подсостояния, каждое из которых может характеризовать неисправность отдельных подсистем, входящих в состав данного устройства.

В языке UML понятие автомата дополнено специальной семантикой входящих в соответствующий пакет элементов. Далее в этой главе будут рассмотрены основные элементы поведения, которые образуют концептуальный базис, необходимый для правильного построения диаграмм состояний.

Формализм обычного автомата основан на выполнении следующих обязательных условий:

1. Автомат не запоминает историю перемещения из состояния в состояние. С точки зрения моделируемого поведения определяющим является сам факт нахождения объекта в том или ином состоянии, но никак не последовательность состояний, в результате которой объект перешел в текущее состояние. Другими словами, автомат «забывает» все состояния, которые предшествовали текущему в данный момент времени. Образно говоря, существует непрозрачная стена, отделяющая текущее состояние от прошлого поведения объекта.

Примечание 50

2. В каждый момент времени автомат может находиться в одном и только в одном из своих состояний. Это означает, что формализм автомата предназначен для моделирования последовательного поведения, когда объект в течение своего жизненного цикла последовательно проходит через все свои состояния. При этом автомат может находиться в отдельном состоянии как угодно долго, если не происходит никаких событий.

Примечание 51

3. Хотя процесс изменения состояний автомата происходит во времени, явно концепция времени не входит в формализм автомата. Это означает, что длительность нахождения автомата в том или ином состоянии, а также время достижения того или иного состояния никак не специфицируются. Другими словами, время на диаграмме состояний присутствует в неявном виде, хотя для отдельных событий может быть указан интервал времени и в явном виде.

Примечание 52

4. Количество состояний автомата должно быть обязательно конечным (в языке UML рассматриваются только конечные автоматы), и все они должны быть специфицированы явным образом. При этом отдельные псевдосостояния могут не иметь спецификаций (начальное и конечное состояния). В этом случае их назначение и семантика полностью определяются из контекста модели и рассматриваемой диаграммы состояний.

Граф автомата не должен содержать изолированных состояний и переходов. Это условие означает, что для каждого из состояний, кроме начального, должно быть определено предшествующее состояние. Каждый переход должен обязательно соединять два состояния автомата. Допускается переход из состояния в себя, такой переход еще называют «петлей».

Автомат не должен содержать конфликтующих переходов, т. е. таких переходов из одного и того же состояния, когда объект одновременно может перейти в два и более последующих состояния (кроме случая параллельных подавтоматов). В языке UML исключение конфликтов возможно на основе введения так называемых сторожевых условий, которые будут рассмотрены ниже.

Таким образом, правила поведения объекта, моделируемого некоторым автоматом, определяются, с одной стороны, общим формализмом автомата, а с другой – его графическим изображением в языке UML в форме конкретной диаграммы состояний.

Данный текст является ознакомительным фрагментом.