12.4. Моделирование правильных треугольных пирамид

12.4. Моделирование правильных треугольных пирамид

Если 3D-модель тетраэдра можно построить по одному параметру, например по длине ребра, то для создания модели правильной треугольной пирамиды требуются два параметра. В наиболее очевидном способе создания 3D-модели первый параметр определяет геометрию основания (равностороннего треугольника), второй параметр задает высоту пирамиды. При использовании пользовательской ориентации Изометрия XYZ и операции По сечениям для создания правильной треугольной пирамиды эскиз 1 в плоскости zx может иметь вид, показанный на рис. 12.39, а, а эскиз 2 (одна точка) в плоскости zy — вид, показанный на рис. 12.39, б.

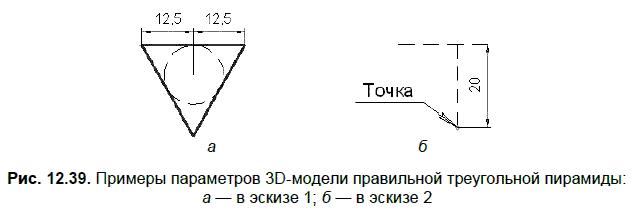
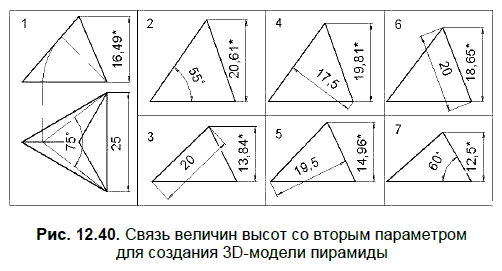
На рис. 12.40 представлены еще 7 способов создания 3D-модели правильной треугольной пирамиды, когда первый параметр — длина ребра основания, равная 25 мм, а вторым параметром является следующая величина:

1. Угол между боковыми гранями (75).

2. Угол между основанием и боковым ребром (55°).

3. Длина бокового ребра (20 мм).

4. Расстояние между скрещивающимися ребрами (17,5 мм).

5. Расстояние между боковой гранью и противолежащей вершиной (19,5 мм).

6. Высота боковой грани (20 мм).

7. Угол между основанием и боковой гранью (60°).

На рис. 12.40 со знаком «*» указан также зависимый параметр — высота пирамиды, построенной по двум заданным параметрам.

Величины высот, показанные на рис. 12.39, могут быть найдены в результате решения элементарных планиметрических задач, или в результате несложных построений с последующим измерением искомой величины.

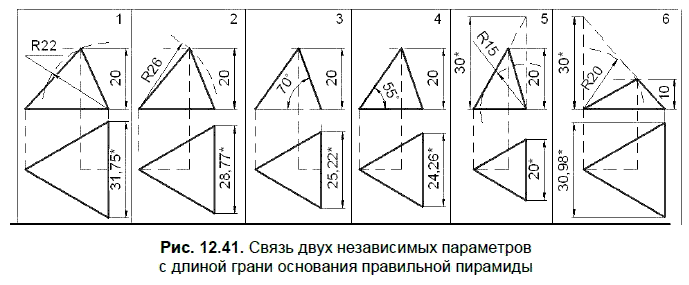
На рис. 12.41 представлены 6 способов создания 3D-модели правильной треугольной пирамиды, когда первый параметр задает высоту пирамиды (например, равную 20 мм), а вторым параметром является следующая величина:

1. Высота боковой грани (22 мм).

2. Длина бокового ребра (26 мм).

3. Угол между основанием и боковой гранью (70°).

4. Угол между основанием и боковым ребром (55°).

5. Расстояние между скрещивающимися ребрами (15 мм).

6. Расстояние между боковой гранью и противолежащей вершиной (20 мм).

На рис. 12.41 со знаком «*» указан также зависимый параметр — длина грани основания пирамиды, построенной по двум заданным параметрам.

Длины ребер основания, показанные на рис. 12.41, могут быть найдены в результате решения планиметрических задач или в результате несложных построений с последующим измерением искомой величины.

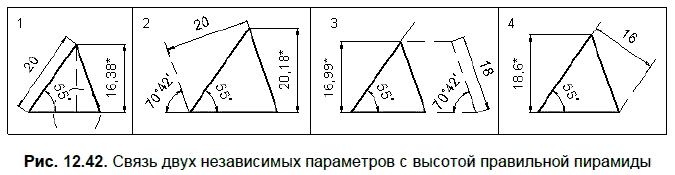
На рис. 12.42 представлены 4 способа создания 3D-модели правильной треугольной пирамиды, когда первый параметр задает угол наклона бокового ребра пирамиды (например, равный 55°), а вторым параметром является следующая величина:

1. Длина бокового ребра (20 мм).

2. Расстояние между боковой гранью и противолежащей вершиной (20 мм).

3. Высота боковой грани (18 мм).

4. Расстояние между скрещивающимися ребрами (16 мм).

На рис. 12.42 со знаком «*» указан также зависимый параметр — высота пирамиды, построенной по двум заданным параметрам.

Пример 12.8

Условие. Создать 3D-модель правильной треугольной пирамиды с параметрами из варианта 1 на рис. 12.42.

Решение. Для создания модели:

1. Выполните команды Файл | Создать | Деталь. В Дереве модели укажите Плоскость ZX.

2. Нажмите кнопку Эскиз на панели Текущее состояние:

3. В появившейся Компактной панели нажмите кнопку переключения Геометрия для вызова соответствующей Инструментальной панели:

-

Выберите команду Непрерывный ввод объектов:

Постройте в эскизе 1 прямоугольный треугольник (для начальных построений в эскизе стиль Основная не использовать). На панели Параметризация выберите команду Вертикальность (рис. 12.43, а) и укажите отрезок, который не должен изменять свое положение при изменении геометрии эскиза 1. Нанесите в эскизе два размера (рис. 12.43, б).

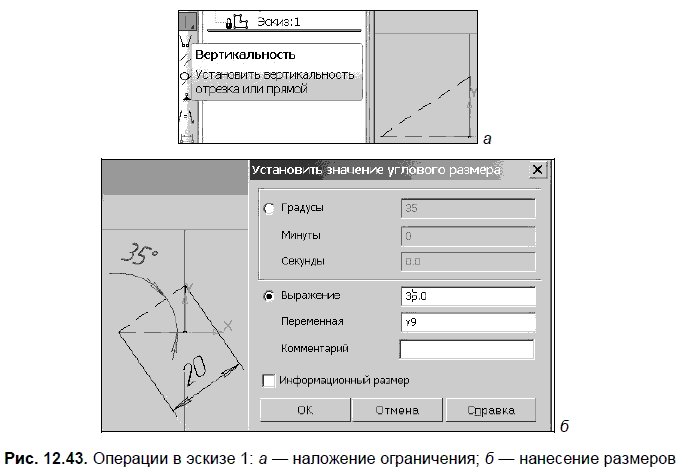
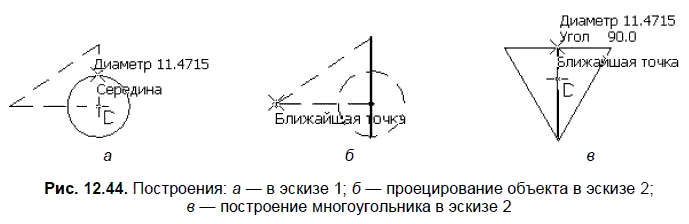
4. На панели Глобальные привязки включите привязку Середина. Используя эту привязку и выбрав команду Окружность, постройте окружность с центром в начале координат и с диаметром, определенным положением середины вертикального катета (рис. 12.44, а). Вертикальный отрезок продолжите до пересечения с нижней частью построенной окружности (рис. 12, 44, б). На панели Геометрия:

выберите команду Точка:

Укажите точку пересечения гипотенузы и горизонтального катета (рис. 12.44, б).

Установите стиль вертикального отрезка: Основная. Завершите эскиз повторным нажатием кнопки Эскиз:

5. В Дереве модели укажите Плоскость XY. Нажмите кнопку Эскиз:

6. В эскизе 2 выполните команды Операции | Спроецировать объект и укажите отрезок из эскиза 1. Измените стиль линии спроецированного отрезка. Выберите команду Многоугольник:

Постройте треугольник с известным центром и привязкой к концам спроецированного в эскиз отрезка (рис. 12.44, в).

7. Закройте эскиз 2 и повторно откройте эскиз 1. Измените стиль Основная вертикального отрезка на любой другой. Закройте эскиз.

8. Нажмите кнопку Операция по сечениям:

на панели Редактирование детали:

9. В Дереве модели укажите Эскиз: 1 и Эскиз: 2 (рис. 12.45).

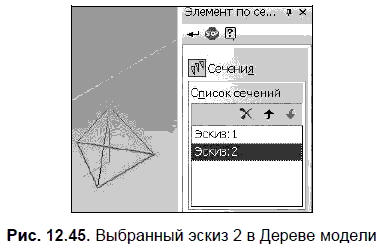
Эти названия появятся в списке сечений Панели свойств. Нажмите кнопку Создать объект:

10. После задания Ориентация | Изометрия YZX и включения команды Невидимые линии тонкие на панели Вид получится изображение тетраэдра, показанное на рис. 12.4, а.

Данный текст является ознакомительным фрагментом.