Оценка

Оценка

Оценка, прежде всего, является предположением. Она не подразумевает никаких обязательств. Вы ничего не обещаете. Нарушение оценки ни в коей мере не повредит вашей репутации. Мы выдаем оценки, прежде всего, потому, что мы не знаем, сколько времени займет работа.

К сожалению, многие разработчики очень слабы в оценках. Дело не в том, что оценка требует какого-то тайного мастерства – вовсе нет. Дело в том, что мы часто не понимаем истинной природы оценки.

Оценка – это не число, а распределение. Возьмем следующий диалог:

Майк: «Сколько, по твоим оценкам, понадобится для завершения работы?»

Питер: «Три дня».

Питер действительно управится с работой за три дня? Возможно, но насколько вероятно? Правильный ответ: понятия не имеем. Что имел в виду Питер и что узнал Майк? Если Майк вернется через три дня и работа не будет выполнена, должен ли он удивляться? А почему, собственно? Питер не давал никаких обязательств. Питер не сказал ему, насколько три дня вероятнее четырех или пяти.

А если бы Майк поинтересовался у Питера, насколько высока вероятность его оценки?

Майк: «Какова вероятность того, что ты справишься за три дня»?

Питер: «Пожалуй, справлюсь».

Майк: «Можешь назвать число?»

Питер: «Пятьдесят или шестьдесят процентов».

Майк: «Значит, есть довольно высокая вероятность, что тебе понадобится четыре дня».

Питер: «Да. Может понадобиться даже пять или шесть, хотя я в этом сомневаюсь».

Майк: «До какой степени сомневаешься?»

Питер: «О, я не знаю… Я на девяносто пять процентов уверен, что работа будет сделана менее чем за шесть дней».

Майк: «То есть может быть и семь?»

Питер: «Ну, если все пойдет наперекосяк… Черт, если все пойдет наперекосяк, может быть десять и даже одиннадцать дней. Но ведь вероятность такого совпадения очень мала, верно?»

Мы постепенно начинаем видеть истину. Оценка Питера представляет собой вероятностное распределение. Своим мысленным взором он видит вероятность завершения задачи так, как показано на рис. 10.1.

Мы видим, почему Питер выдал исходную оценку в 3 дня – это самый высокий столбец гистограммы. Соответственно, Питеру она представляется наиболее вероятной продолжительностью выполнения задачи.

Но Майк смотрит на происходящее иначе. Он обращает внимание на правый край распределения и беспокоится о том, что Питеру может понадобиться более 11 дней.

Должен ли Майк беспокоиться об этом? Конечно! Закона Мерфи[42] еще никто не отменял, поэтому могут возникнуть непредвиденные осложнения.

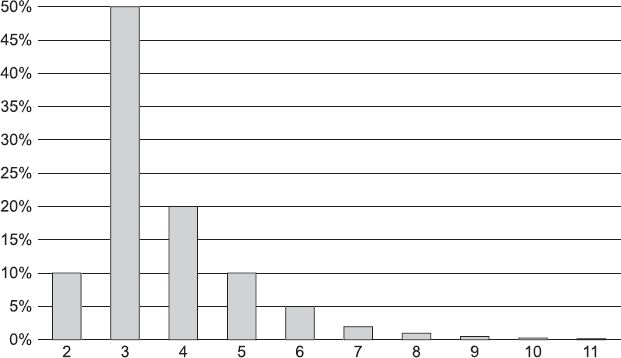
Рис. 10.1. Вероятностное распределение

Данный текст является ознакомительным фрагментом.