2. Операции декартового произведения и естественного соединения

2. Операции декартового произведения и естественного соединения

Операция декартового произведения и операция естественного соединения являются бинарными операциями типа произведения и основываются на операции объединения двух отношений, которую мы рассматривали ранее.

Хотя действие операции декартова произведения многим может показаться знакомым, начнем мы все-таки с операции естественного произведения, так как она является более общим случаем, нежели первая операция.

Итак, рассмотрим операцию естественного соединения. Следует сразу заметить, что операндами этого действия могут являться отношения с разными схемами в отличие от трех бинарных операций объединения, пересечения и переименования.

Если рассмотреть два отношения с различными схемами отношений r1(S1) и r2(S2), то их естественным соединением будет новое отношение r3(S3), которое будет состоять только из тех кортежей операндов, которые совпадают на пересечении схем отношений. Соответственно, схема нового отношения будет больше любой из схем отношений исходных, так как является их соединением, «склеиванием». Кстати, кортежи, одинаковые в двух отношениях-операндах, по которым и происходит это «склеивание», называются соединимыми.

Запишем определение операции естественного соединения на языке формул систем управления базами данных:

r3(S3) = r1(S1) ? r2(S2) = {t(S1 ?S2) | t[S1] ? r1 & t(S2) ? r2};

Рассмотрим пример, хорошо иллюстрирующий работу естественного соединения, его «склеивание». Пусть дано два отношения r1(S1) и r2(S2), в табличной форме представления соответственно равные:

r1(S1):

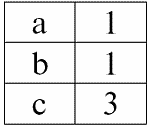
r2(S2):

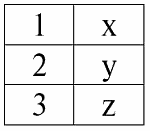
Мы видим, что у этих отношений присутствуют кортежи, совпадающие при пересечении схем S1 и S2 отношений. Перечислим их:

1) кортеж {a, 1} отношения r1(S1) совпадает с кортежем {1, x} отношения r2(S2);

2) кортеж {b, 1} из r1(S1) также совпадает с кортежем {1, x} из r2(S2);

3) кортеж {c, 3} совпадает с кортежем {3, z}.

Значит, при естественном соединении новое отношение r3(S3) получается «склеиванием» именно на этих кортежах. Таким образом, r3(S3) в табличном представлении будет выглядеть следующим образом:

r3(S3) = r1(S1) ? r2(S2):

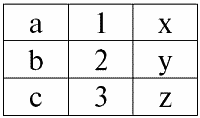
Получается по определению: схема S3 не совпадает ни со схемой S1, ни со схемой S2, мы «склеили» две исходные схемы по пересекающимся кортежам, чтобы получить их естественное соединение.

Покажем схематично, как происходит соединение кортежей при применении операции естественного соединения.

Пусть отношение r1 имеет условный вид:

А отношение r2 – вид:

Тогда их естественное соединение будет выглядеть следующим образом:

Видим, что «склеивание» отношений-операндов происходит по той самой схеме, что мы приводили ранее, рассматривая пример.

Операция декартового соединения является частным случаем операции естественного соединения. Если конкретнее, то, рассматривая действие операции декартового произведения на отношения, мы заведомо оговариваем, что в этом случае может идти речь только о непересекающихся схемах отношений. В результате применения обеих операций получаются отношения со схемами, равными объединению схем отношений-операндов, только в декартово произведение двух отношений попадают всевозможные пары их кортежей, так как схемы операндов ни в коем случае не должны пересекаться.

Таким образом, исходя из всего вышесказанного запишем математическую формулу для операции декартового произведения:

r4(S4) = r1(S1) ? r2(S2) = {t(S1 ? S2) | t [S1] ? r1 & t(S2) ? r2}, S1 ? S2= ?;

Теперь рассмотрим пример, чтобы показать, какой вид будет иметь результирующая схема отношения, при применении операции декартового произведения.

Пусть даны два отношения r1(S1) и r2(S2), которые в табличном виде представляются следующим образом:

r1(S1):

r2(S2):

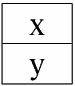
Итак, мы видим, что ни один из кортежей отношений r1(S1) и r2(S2), действительно, не совпадает в их пересечении. Поэтому в результирующее отношение r4(S4) попадут всевозможные пары кортежей первого и второго отношений-операндов. Получится:

r4(S4) = r1(S1) ? r2(S2):

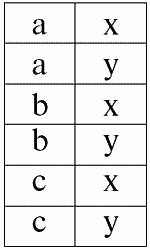
Получилась новая схема отношения r4(S4) не «склеиванием» кортежей как в предыдущем случае, а перебором всех возможных различных пар несовпадающих в пересечении исходных схем кортежей.

Снова, как и в случае естественного соединения, приведем схематичный пример работы операции декартового произведения.

Пусть r1 задано следующим условным образом:

А отношение r2 задано:

Тогда их декартовое произведение схематично можно изобразить следующим образом:

Именно таким образом и получается результирующее отношение при применении операции декартового произведения.

Более 800 000 книг и аудиокниг! 📚

Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением

ПОЛУЧИТЬ ПОДАРОК

Данный текст является ознакомительным фрагментом.