2. Арифметические команды
2. Арифметические команды
Микропроцессор может выполнять целочисленные операции и операции с плавающей точкой. Для этого в его архитектуре есть два отдельных блока:
1) устройство для выполнения целочисленных операций;
2) устройство для выполнения операций с плавающей точкой.
Каждое из этих устройств имеет свою систему команд. В принципе, целочисленное устройство может взять на себя многие функции устройства с плавающей точкой, но это потребует больших вычислительных затрат. Для большинства задач, использующих язык ассемблера, достаточно целочисленной арифметики.
Обзор группы арифметических команд и данных
Целочисленное вычислительное устройство поддерживает чуть больше десятка арифметических команд. На рисунке 27 приведена классификация команд этой группы.
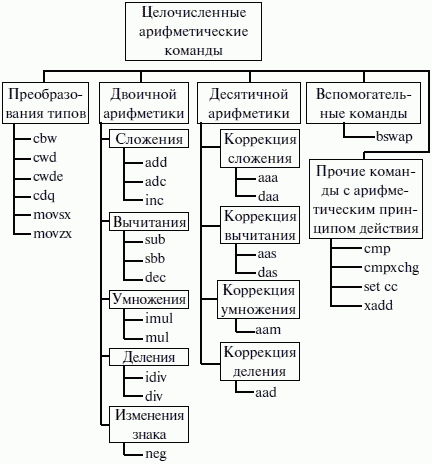
Рис. 27. Классификация арифметических команд
Группа арифметических целочисленных команд работает с двумя типами чисел:
1) целыми двоичными числами. Числа могут иметь знаковый разряд или не иметь такового, т. е. быть числами со знаком или без знака;
2) целыми десятичными числами.
Рассмотрим машинные форматы, в которых хранятся эти типы данных.
Целые двоичные числа
Целое двоичное число с фиксированной точкой – это число, закодированное в двоичной системе счисления.
Размерность целого двоичного числа может составлять 8, 16 или 32 бит. Знак двоичного числа определяется тем, как интерпретируется старший бит в представлении числа. Это 7,15 или 31-й биты для чисел соответствующей размерности. При этом интересно то, что среди арифметических команд есть всего две команды, которые действительно учитывают этот старший разряд как знаковый, – это команды целочисленного умножения и деления imul и idiv. В остальных случаях ответственность за действия со знаковыми числами и, соответственно, со знаковым разрядом ложится на программиста. Диапазон значений двоичного числа зависит от его размера и трактовки старшего бита либо как старшего значащего бита числа, либо как бита знака числа (табл. 9).
Таблица 9. Диапазон значений двоичных чисел
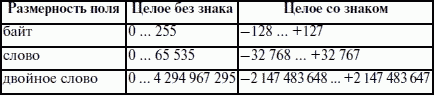
Десятичные числа
Десятичные числа – специальный вид представления числовой информации, в основу которого положен принцип кодирования каждой десятичной цифры числа группой из четырех бит. При этом каждый байт числа содержит одну или две десятичные цифры в так называемом двоично-десятичном коде (BCD – Binary-Coded Decimal). Микропроцессор хранит BCD-числа в двух форматах (рис. 28):
1) упакованном формате. В этом формате каждый байт содержит две десятичные цифры. Десятичная цифра представляет собой двоичное значение в диапазоне от 0 до 9 размером 4 бита. При этом код старшей цифры числа занимает старшие 4 бита. Следовательно, диапазон представления десятичного упакованного числа в 1 байте составляет от 00 до 99;
2) неупакованном формате. В этом формате каждый байт содержит одну десятичную цифру в четырех младших битах. Старшие 4 бита имеют нулевое значение. Это так называемая зона. Следовательно, диапазон представления десятичного неупакованного числа в 1 байте составляет от 0 до 9.
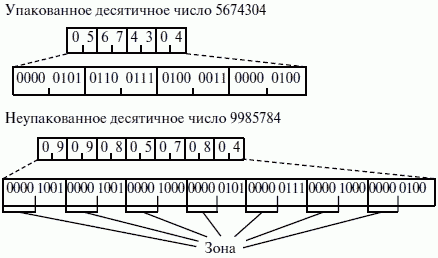
Рис. 28. Представление BCD-чисел
Как описать двоично-десятичные числа в программе? Для этого можно использовать только две директивы описания и инициализации данных – db и dt. Возможность применения только этих директив для описания BCD-чисел обусловлена тем, что к таким числам также применим принцип «младший байт по младшему адресу», что очень удобно для их обработки. И вообще, при использовании такого типа данных как BCD-числа, порядок описания этих чисел в программе и алгоритм их обработки – это дело вкуса и личных пристрастий программиста. Это станет ясно после того, как мы ниже рассмотрим основы работы с BCD-числами.
Арифметические операции над целыми двоичными числами
Сложение двоичных чисел без знака
Микропроцессор выполняет сложение операндов по правилам сложения двоичных чисел. Проблем не возникает до тех пор, пока значение результата не превышает размерности поля операнда. Например, при сложении операндов размером в байт результат не должен превышать число 255. Если это происходит, то результат оказывается неверным. Рассмотрим, почему так происходит.
К примеру, выполним сложение: 254 + 5 = 259 в двоичном виде. 11111110 + 0000101 = 1 00000011. Результат вышел за пределы 8 бит и правильное его значение укладывается в 9 бит, а в 8-битовом поле операнда осталось значение 3, что, конечно, неверно. В микропроцессоре этот исход сложения прогнозируется и предусмотрены специальные средства для фиксирования подобных ситуаций и их обработки. Так, для фиксирования ситуации выхода за разрядную сетку результата, как в данном случае, предназначен флаг переноса cf. Он располагается в бите 0 регистра флагов EFLAGS/FLAGS. Именно установкой этого флага фиксируется факт переноса единицы из старшего разряда операнда. Естественно, что программист должен учитывать возможность такого исхода операции сложения и предусматривать средства для корректировки. Это предполагает включение участков кода после операции сложения, в которых анализируется флаг cf. Анализ этого флага можно провести различными способами.
Самый простой и доступный – использовать команду условного перехода jcc. Эта команда в качестве операнда имеет имя метки в текущем сегменте кода. Переход на эту метку осуществляется в случае, если в результате работы предыдущей команды флаг cf установился в 1. В системе команд микропроцессора имеются три команды двоичного сложения:
1) inc операнд – операция инкремента, т. е. увеличения значения операнда на 1;
2) add операнд_1, операнд_2 – команда сложения с принципом действия: операнд_1 = операнд_1 + операнд_2;
3) adc операнд_1, операнд_2 – команда сложения с учетом флага переноса cf. Принцип действия команды: операнд_1 = операнд_1 + операнд_2 + значение_сГ.
Обратите внимание на последнюю команду – это команда сложения, учитывающая перенос единицы из старшего разряда. Механизм появления такой единицы мы уже рассмотрели. Таким образом, команда adc является средством микропроцессора для сложения длинных двоичных чисел, размерность которых превосходит поддерживаемые микропроцессором длины стандартных полей.
Сложение двоичных чисел со знаком
На самом деле микропроцессор «не подозревает» о различии между числами со знаком и без знака. Вместо этого у него есть средства фиксирования возникновения характерных ситуаций, складывающихся в процессе вычислений. Некоторые из них мы рассмотрели при обсуждении сложения чисел без знака:
1) флаг переноса cf, установка которого в 1 говорит о том, что произошел выход за пределы разрядности операндов;
2) команду adc, которая учитывает возможность такого выхода (перенос из младшего разряда).
Другое средство – это регистрация состояния старшего (знакового) разряда операнда, которое осуществляется с помощью флага переполнения of в регистре EFLAGS (бит 11).
Вы, конечно, помните, как представляются числа в компьютере: положительные – в двоичном коде, отрицательные – в дополнительном коде. Рассмотрим различные варианты сложения чисел. Примеры призваны показать поведение двух старших битов операндов и правильность результата операции сложения.
Пример
30566 = 0111011101100110
+
00687 = 00000010 10101111
=
31253 = 01111010 00010101
Следим за переносами из 14 и 15-го разрядов и правильностью результата: переносов нет, результат правильный.
Пример
30566 = 0111011101100110
+
30566 = 0111011101100110
=
1132 = 11101110 11001100
Произошел перенос из 14-го разряда; из 15-го разряда переноса нет. Результат неправильный, так как имеется переполнение – значение числа получилось больше, чем то, которое может иметь 16-битное число со знаком (+32 767).
Пример
-30566 = 10001000 10011010
+
-04875 = 11101100 11110101
=
-35441 = 01110101 10001111
Произошел перенос из 15-го разряда, из 14-го разряда нет переноса. Результат неправильный, так как вместо отрицательного числа получилось положительное (в старшем бите находится 0).
Пример
-4875 = 11101100 11110101
+
-4875 = 11101100 11110101
=
09750 = 11011001 11101010
Есть переносы из 14 и 15-го разрядов. Результат правильный.
Таким образом, мы исследовали все случаи и выяснили, что ситуация переполнения (установка флага OF в 1) происходит при переносе:
1) из 14-го разряда (для положительных чисел со знаком);
2) из 15-го разряда (для отрицательных чисел).
И наоборот, переполнения не происходит (т. е. флаг OF сбрасывается в 0), если есть перенос из обоих разрядов или перенос отсутствует в обоих разрядах.
Итак, переполнение регистрируется с помощью флага переполнения of. Дополнительно к флагу of при переносе из старшего разряда устанавливается в 1 и флаг переноса CF Так как микропроцессор не знает о существовании чисел со знаком и без знака, то вся ответственность за правильность действий с получившимися числами ложится на программиста. Проанализировать флаги CF и OF можно командами условного перехода JCJNC и JOJNO соответственно.
Что же касается команд сложения чисел со знаком, то они те же, что и для чисел без знака.
Вычитание двоичных чисел без знака
Как и при анализе операции сложения, порассуждаем над сутью процессов, происходящих при выполнении операции вычитания. Если уменьшаемое больше вычитаемого, то проблем нет, – разность положительна, результат верен. Если уменьшаемое меньше вычитаемого, возникает проблема: результат меньше 0, а это уже число со знаком. В этом случае результат необходимо завернуть. Что это означает? При обычном вычитании (в столбик) делают заем 1 из старшего разряда. Микропроцессор поступает аналогично, т. е. занимает 1 из разряда, следующего за старшим, в разрядной сетке операнда. Поясним на примере.
Пример
05 = 00000000 00000101
-10 = 00000000 00001010
Для того чтобы произвести вычитание, произведем
воображаемый заем из старшего разряда:
100000000 00000101
-
00000000 00001010
=
11111111 11111011
Тем самым, по сути, выполняется действие
(65 536 + 5) – 10 = 65 531
0 здесь как бы эквивалентен числу 65536. Результат, конечно, неверен, но микропроцессор считает, что все нормально, хотя факт заема единицы он фиксирует установкой флага переноса cf. Но посмотрите еще раз внимательно на результат операции вычитания. Это же -5 в дополнительном коде! Проведем эксперимент: представим разность в виде суммы 5 + (-10).
Пример
5 = 00000000 00000101
+
(-10)= 11111111 11110110
=
11111111 11111011
т. е. мы получили тот же результат, что и в предыдущем примере.
Таким образом, после команды вычитания чисел без знака нужно анализировать состояние флага СЕ Если он установлен в 1, то это говорит о том, что произошел заем из старшего разряда и результат получился в дополнительном коде.
Аналогично командам сложения группа команд вычитания состоит из минимально возможного набора. Эти команды выполняют вычитание по алгоритмам, которые мы сейчас рассматриваем, а учет особых ситуаций должен производиться самим программистом. К командам вычитания относятся следующие:
1) dec операнд – операция декремента, т. е. уменьшения значения операнда на 1;
2) sub операнд_1, операнд_2 – команда вычитания; ее принцип действия: операнд_1 = операнд_1 – операнд_2;
3) sbb операнд_1, операнд_2 – команда вычитания с учетом заема (флага ci): операнд_1 = операнд_1 – операнд_2 – значение_сГ.
Как видите, среди команд вычитания есть команда sbb, учитывающая флаг переноса cf. Эта команда подобна adc, но теперь уже флаг cf исполняет роль индикатора заема 1 из старшего разряда при вычитании чисел.
Вычитание двоичных чисел со знаком
Здесь все несколько сложнее. Микропроцессору незачем иметь два устройства – сложения и вычитания. Достаточно наличия только одного – устройства сложения. Но для вычитания способом сложения чисел со знаком в дополнительном коде необходимо представлять оба операнда – и уменьшаемое, и вычитаемое. Результат тоже нужно рассматривать как значение в дополнительном коде. Но здесь возникают сложности. Прежде всего они связаны с тем, что старший бит операнда рассматривается как знаковый. Рассмотрим пример вычитания 45 – (-127).
Пример
Вычитание чисел со знаком 1
45 = 0010 1101
-
-127 = 1000 0001
=
-44 = 1010 1100
Судя по знаковому разряду, результат получился отрицательный, что, в свою очередь, говорит о том, что число нужно рассматривать как дополнение, равное —44. Правильный результат должен быть равен 172. Здесь мы, как и в случае знакового сложения, встретились с переполнением мантиссы, когда значащий разряд числа изменил знаковый разряд операнда. Отследить такую ситуацию можно по содержимому флага переполнения of. Его установка в 1 говорит о том, что результат вышел за диапазон представления знаковых чисел (т. е. изменился старший бит) для операнда данного размера, и программист должен предусмотреть действия по корректировке результата.
Пример
Вычитание чисел со знаком 2
-45–45 = -45 + (-45)= -90.
-45 = 11010011
+
-45 = 11010011
=
-90 = 1010 0110
Здесь все нормально, флаг переполнения of сброшен в 0, а 1 в знаковом разряде говорит о том, что значение результата – число в дополнительном коде.
Вычитание и сложение операндов большой размерности
Если вы заметили, команды сложения и вычитания работают с операндами фиксированной размерности: 8, 16, 32 бит. А что делать, если нужно сложить числа большей размерности, например 48 бит, используя 16-разрядные операнды? К примеру, сложим два 48-разрядных числа:
Рис. 29. Сложение операндов большой размерности
На рисунке 29 по шагам показана технология сложения длинных чисел. Видно, что процесс сложения многобайтных чисел происходит так же, как и при сложении двух чисел «в столбик», – с осуществлением при необходимости переноса 1 в старший разряд. Если нам удастся запрограммировать этот процесс, то мы значительно расширим диапазон двоичных чисел, над которыми мы сможем выполнять операции сложения и вычитания.
Принцип вычитания чисел с диапазоном представления, превышающим стандартные разрядные сетки операндов, тот же, что и при сложении, т. е. используется флаг переноса cf. Нужно только представлять себе процесс вычитания в столбик и правильно комбинировать команды микропроцессора с командой sbb.
В завершение обсуждения команд сложения и вычитания отметим, что кроме флагов cf и of в регистре eflags есть еще несколько флагов, которые можно использовать с двоичными арифметическими командами. Речь идет о следующих флагах:
1) zf – флаг нуля, который устанавливается в 1, если результат операции равен 0, и в 1, если результат не равен 0;
2) sf – флаг знака, значение которого после арифметических операций (и не только) совпадает со значением старшего бита результата, т. е. с битом 7, 15 или 31. Таким образом, этот флаг можно использовать для операций над числами со знаком.
Умножение чисел без знака
Для умножения чисел без знака предназначена команда
mul сомножитель_1
Как видите, в команде указан всего лишь один операнд-сомножитель. Второй операнд-сомножитель_2 задан неявно. Его местоположение фиксировано и зависит от размера сомножителей. Так как в общем случае результат умножения больше, чем любой из его сомножителей, то его размер и местоположение должны быть тоже определены однозначно. Варианты размеров сомножителей и размещения второго операнда и результата приведены в таблице 10.
Таблица 10. Расположение операндов и результата при умножении
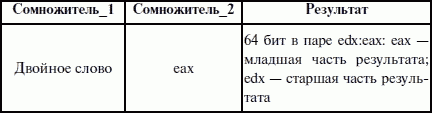
Из таблицы видно, что произведение состоит из двух частей и в зависимости от размера операндов размещается в двух местах – на месте сомножитель_2 (младшая часть) и в дополнительном регистре ah, dx, edx (старшая часть). Как же динамически (т. е. во время выполнения программы) узнать, что результат достаточно мал и уместился в одном регистре или что он превысил размерность регистра и старшая часть оказалась в другом регистре? Для этого привлекаются уже известные нам по предыдущему обсуждению флаги переноса cf и переполнения of:
1) если старшая часть результата нулевая, то после операции произведения флаги cf = 0 и of = 0;
2) если же эти флаги ненулевые, то это означает, что результат вышел за пределы младшей части произведения и состоит из двух частей, что и нужно учитывать при дальнейшей работе.
Умножение чисел со знаком
Для умножения чисел со знаком предназначена команда
[imul операнд_1, операнд_2, операнд_3]
Эта команда выполняется так же, как и команда mul. Отличительной особенностью команды imul является только формирование знака.
Если результат мал и умещается в одном регистре (т. е. если cf = of = 0), то содержимое другого регистра (старшей части) является расширением знака – все его биты равны старшему биту (знаковому разряду) младшей части результата. В противном случае (если cf = of = 1) знаком результата является знаковый бит старшей части результата, а знаковый бит младшей части является значащим битом двоичного кода результата.
Деление чисел без знака
Для деления чисел без знака предназначена команда
div делитель
Делитель может находиться в памяти или в регистре и иметь размер 8, 16 или 32 бит. Местонахождение делимого фиксировано и так же, как в команде умножения, зависит от размера операндов. Результатом команды деления являются значения частного и остатка.
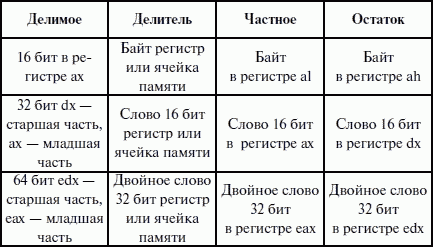
Варианты местоположения и размеров операндов операции деления показаны в таблице 11.
Таблица 11. Расположение операндов и результата при делении
После выполнения команды деления содержимое флагов неопределенно, но возможно возникновение прерывания с номером 0, называемого «деление на нуль». Этот вид прерывания относится к так называемым исключениям. Эта разновидность прерываний возникает внутри микропроцессора из-за некоторых аномалий во время вычислительного процесса. Прерывание О, «деление на нуль», при выполнении команды div может возникнуть по одной из следующих причин:
1) делитель равен нулю;
2) частное не входит в отведенную под него разрядную сетку, что может произойти в следующих случаях:
а) при делении делимого величиной в слово на делитель величиной в байт, причем значение делимого в более чем 256 раз больше значения делителя;
б) при делении делимого величиной в двойное слово на делитель величиной в слово, причем значение делимого в более чем 65 536 раз больше значения делителя;
в) при делении делимого величиной в учетверенное слово на делитель величиной в двойное слово, причем значение делимого в более чем 4 294 967 296 раз больше значения делителя.
Деление чисел со знаком
Для деления чисел со знаком предназначена команда
idiv делитель
Для этой команды справедливы все рассмотренные положения, касающиеся команд и чисел со знаком. Отметим лишь особенности возникновения исключения 0, «деление на нуль», в случае чисел со знаком. Оно возникает при выполнении команды idiv по одной из следующих причин:
1) делитель равен нулю;
2) частное не входит в отведенную для него разрядную сетку.
Последнее в свою очередь может произойти:
1) при делении делимого величиной в слово со знаком на делитель величиной в байт со знаком, причем значение делимого в более чем 128 раз больше значения делителя (таким образом, частное не должно находиться вне диапазона от —128 до + 127);
2) при делении делимого величиной в двойное слово со знаком на делитель величиной в слово со знаком, причем значение делимого в более чем 32 768 раз больше значения делителя (таким образом, частное не должно находиться вне диапазона от —32 768 до +32 768);
3) при делении делимого величиной в учетверенное слово со знаком на делитель величиной в двойное слово со знаком, причем значение делимого в более чем 2 147 483 648 раз больше значения делителя (таким образом, частное не должно находиться вне диапазона от —2 147 483 648 до +2 147 483 647).
Вспомогательные команды для целочисленных операций
В системе команд микропроцессора есть несколько команд, которые могут облегчить программирование алгоритмов, производящих арифметические вычисления. В них могут возникать различные проблемы, для разрешения которых разработчики микропроцессора предусмотрели несколько команд.
Команды преобразования типов
Что делать, если размеры операндов, участвующих в арифметических операциях, разные? Например, предположим, что в операции сложения один операнд является словом, а другой занимает двойное слово. Выше сказано, что в операции сложения должны участвовать операнды одного формата. Если числа без знака, то выход найти просто. В этом случае можно на базе исходного операнда сформировать новый (формата двойного слова), старшие разряды которого просто заполнить нулями. Сложнее ситуация для чисел со знаком: как динамически, в ходе выполнения программы, учесть знак операнда? Для решения подобных проблем в системе команд микропроцессора есть так называемые команды преобразования типа. Эти команды расширяют байты в слова, слова – в двойные слова и двойные слова – в учетверенные слова (64-разрядные значения). Команды преобразования типа особенно полезны при преобразовании целых со знаком, так как они автоматически заполняют старшие биты вновь формируемого операнда значениями знакового бита старого объекта. Эта операция приводит к целым значениям того же знака и той же величины, что и исходная, но уже в более длинном формате. Подобное преобразование называется операцией распространения знака.
Существуют два вида команд преобразования типа.
1. Команды без операндов. Эти команды работают с фиксированными регистрами:
1) cbw (Convert Byte to Word) – команда преобразования байта (в регистре al) в слово (в регистре ах) путем распространения значения старшего бита al на все биты регистра ah;
2) cwd (Convert Word to Double) – команда преобразования слова (в регистре ах) в двойное слово (в регистрах dx: ax) путем распространения значения старшего бита ах на все биты регистра dx;
3) cwde (Convert Word to Double) – команда преобразования слова (в регистре ах) в двойное слово (в регистре еах) путем распространения значения старшего бита ах на все биты старшей половины регистра еах;
4) cdq (Convert Double Word to Quarter Word) – команда преобразования двойного слова (в регистре еах) в учетверенное слово (в регистрах edx: eax) путем распространения значения старшего бита еах на все биты регистра edx.
2. Команды movsx и movzx, относящиеся к командам обработки строк. Эти команды обладают полезным свойством в контексте нашей проблемы:
1) movsx операнд_1, операнд_2 – переслать с распространением знака. Расширяет 8 или 16-разрядное значение операнд_2, которое может быть регистром или операндом в памяти, до 16 или 32-разрядного значения в одном из регистров, используя значение знакового бита для заполнения старших позиций операнд_1. Данную команду удобно использовать для подготовки операндов со знаками к выполнению арифметических действий;
2) movzx операнд_1, операнд_2 – переслать с расширением нулем. Расширяет 8– или 16-разрядное значение операнд_2 до 16– или 32-разрядного с очисткой (заполнением) нулями старших позиций операнд_2. Данную команду удобно использовать для подготовки операндов без знака к выполнению арифметических действий.
Другие полезные команды
1. xadd назначение, источник – обмен местами и сложение.
Команда позволяет выполнить последовательно два действия:
1) обменять значения назначение и источник;
2) поместить на место операнда назначение сумму: назначение = назначение + источник.
2. neg операнд – отрицание с дополнением до двух.
Команда выполняет инвертирование значения операнд. Физически команда выполняет одно действие:
операнд = 0 – операнд, т. е. вычитает операнд из нуля.
Команду neg операнд можно применять:
1) для смены знака;
2) для выполнения вычитания из константы.
Арифметические операции над двоично-десятичными числами
В данном разделе мы рассмотрим особенности каждого из четырех основных арифметических действий для упакованных и неупакованных двоично-десятичных чисел.
Справедливо может возникнуть вопрос: а зачем нужны BCD-числа? Ответ может быть следующим: BCD-числа нужны в деловых приложениях, т. е. там, где числа должны быть большими и точными. Как мы уже убедились на примере двоичных чисел, операции с такими числами довольно проблематичны для языка ассемблера. К недостаткам использования двоичных чисел можно отнести следующие:
1) значения величин в формате слова и двойного слова имеют ограниченный диапазон. Если программа предназначена для работы в области финансов, то ограничение суммы в рублях величиной 65 536 (для слова) или даже 4 294 967 296 (для двойного слова) будет существенно сужать сферу ее применения;
2) наличие ошибок округления. Представляете себе программу, работающую где-нибудь в банке, которая не учитывает величину остатка при действиях с целыми двоичными числами и оперирует при этом миллиардами? Не хотелось бы быть автором такой программы. Применение чисел с плавающей точкой не спасет – там существует та же проблема округления;
3) представление большого объема результатов в символьном виде (ASCII-коде). Деловые программы не просто выполняют вычисления; одной из целей их использования является оперативная выдача информации пользователю. Для этого, естественно, информация должна быть представлена в символьном виде. Перевод чисел из двоичного кода в ASCII-код требует определенных вычислительных затрат. Число с плавающей точкой еще труднее перевести в символьный вид. А вот если посмотреть на шестнадцатеричное представление неупакованной десятичной цифры и на соответствующий ей символ в таблице ASCII, то видно, что они отличаются на величину 30h. Таким образом, преобразование в символьный вид и обратно получается намного проще и быстрее.
Наверное вы уже убедились в важности овладения хотя бы основами действий с десятичными числами. Далее рассмотрим особенности выполнения основных арифметических операций с десятичными числами. Отметим сразу тот факт, что отдельных команд сложения, вычитания, умножения и деления BCD-чисел нет. Сделано это по вполне понятным причинам: размерность таких чисел может быть сколь угодно большой. Складывать и вычитать можно двоично-десятичные числа, как в упакованном формате, так и в неупакованном, а вот делить и умножать можно только неупакованные BCD-числа. Почему это так, будет видно из дальнейшего обсуждения.
Арифметические действия над неупакованными BCD-числами
Сложение неупакованных BCD-чисел
Рассмотрим два случая сложения.
Пример
Результат сложения не больше 9
6 = 0000 0110
+
3 = 0000 0011
=
9 = 0000 1001
Переноса из младшей тетрады в старшую нет. Результат правильный.
Пример
Результат сложения больше 9:
06 = 0000 0110
+
07 = 0000 0111
=
13 = 0000 1101
Мы получили уже не BCD-число. Результат неправильный. Правильный результат в неупакованном BCD-формате должен быть таким: 0000 0001 0000 0011 в двоичном представлении (или 13 в десятичном).
Проанализировав данную проблему при сложении BCD-чисел (и подобные проблемы при выполнении других арифметических действий) и возможные пути ее решения, разработчики системы команд микропроцессора решили не вводить специальные команды для работы с BCD-числами, а ввести несколько корректировочных команд.
Назначение этих команд – в корректировке результата работы обычных арифметических команд для случаев, когда операнды в них являются BCD-числами.
В случае вычитания в примере 10 видно, что полученный результат нужно корректировать. Для коррекции операции сложения двух однозначных неупакованных BCD-чисел в системе команд микропроцессора существует специальная команда – ааа (ASCII Adjust for Addition) – коррекция результата сложения для представления в символьном виде.
Эта команда не имеет операндов. Она работает неявно только с регистром al и анализирует значение его младшей тетрады:
1) если это значение меньше 9, то флаг cf сбрасывается в О и осуществляется переход к следующей команде;
2) если это значение больше 9, то выполняются следующие действия:
а) к содержимому младшей тетрады al (но не к содержимому всего регистра!) прибавляется 6, тем самым значение десятичного результата корректируется в правильную сторону;
б) флаг cf устанавливается в 1, тем самым фиксируется перенос в старший разряд, для того чтобы его можно было учесть в последующих действиях.
Так, в примере 10, предполагая, что значение суммы 0000 1101 находится в al, после команды ааа в регистре будет 1101 + 0110 = 0011, т. е. двоичное 0000 0011 или десятичное 3, а флаг cf установится в 1, т. е. перенос запомнился в микропроцессоре. Далее программисту нужно будет использовать команду сложения adc, которая учтет перенос из предыдущего разряда.
Вычитание неупакованных BCD-чисел
Ситуация здесь вполне аналогична сложению. Рассмотрим те же случаи.
Пример
Результат вычитания не больше 9:
6 = 0000 0110
-
3 = 0000 0011
=
3 = 0000 0011
Как видим, заема из старшей тетрады нет. Результат верный и корректировки не требует.
Пример
Результат вычитания больше 9:
6 = 0000 0110
-
7 = 0000 0111
=
-1 = 1111 1111
Вычитание проводится по правилам двоичной арифметики. Поэтому результат не является BCD-числом.
Правильный результат в неупакованном BCD-формате должен быть 9 (0000 1001 в двоичной системе счисления). При этом предполагается заем из старшего разряда, как при обычной команде вычитания, т. е. в случае с BCD числами фактически должно быть выполнено вычитание 16 – 7. Таким образом, видно: как и в случае сложения, результат вычитания нужно корректировать. Для этого существует специальная команда – aas (ASCII Adjust for Substraction) – коррекция результата вычитания для представления в символьном виде.
Команда aas также не имеет операндов и работает с регистром al, анализируя его младшую тетраду следующим образом:
1) если ее значение меньше 9, то флаг cf сбрасывается в 0 и управление передается следующей команде;
2) если значение тетрады в al больше 9, то команда aas выполняет следующие действия:
а) из содержимого младшей тетрады регистра al (заметьте – не из содержимого всего регистра) вычитает 6;
б) обнуляет старшую тетраду регистра al;
в) устанавливает флаг cf в 1, тем самым фиксируя воображаемый заем из старшего разряда.
Понятно, что команда aas применяется вместе с основными командами вычитания sub и sbb. При этом команду sub есть смысл использовать только один раз, при вычитании самых младших цифр операндов, далее должна применяться команда sbb, которая будет учитывать возможный заем из старшего разряда.
Умножение неупакованных BCD-чисел
На примере сложения и вычитания неупакованных чисел стало понятно, что стандартных алгоритмов для выполнения этих действий над BCD-числами нет и программист должен сам, исходя из требований к своей программе, реализовать эти операции.
Реализация двух оставшихся операций – умножения и деления – еще более сложна. В системе команд микропроцессора присутствуют только средства для производства умножения и деления одноразрядных неупакованных BCD-чисел.
Для того чтобы умножать числа произвольной размерности, нужно реализовать процесс умножения самостоятельно, взяв за основу некоторый алгоритм умножения, например «в столбик».
Для того чтобы перемножить два одноразрядных BCD-числа, необходимо:
1) поместить один из сомножителей в регистр AL (как того требует команда mul);
2) поместить второй операнд в регистр или память, отведя байт;
3) перемножить сомножители командой mul (результат, как и положено, будет в ах);
4) результат, конечно, получится в двоичном коде, поэтому его нужно скорректировать.
Для коррекции результата после умножения применяется специальная команда – aam (ASCII Adjust for Multiplication) – коррекция результата умножения для представления в символьном виде.
Она не имеет операндов и работает с регистром АХ следующим образом:
1) делит al на 10;
2) результат деления записывается так: частное в al, остаток в ah. В результате после выполнения команды aam в регистрах AL и ah находятся правильные двоично-десятичные цифры произведения двух цифр.
Перед окончанием обсуждения команды aam необходимо отметить еще один вариант ее применения. Эту команду можно применять для преобразования двоичного числа в регистре AL в неупакованное BCD-число, которое будет размещено в регистре ах: старшая цифра результата в ah, младшая – в al. Понятно, что двоичное число должно быть в диапазоне 0… 99.
Деление неупакованных BCD-чисел
Процесс выполнения операции деления двух неупакованных BCD-чисел несколько отличается от других, рассмотренных ранее операций с ними. Здесь также требуются действия по коррекции, но они должны осуществляться до основной операции, выполняющей непосредственно деление одного BCD-числа на другое BCD-число. Предварительно в регистре ах нужно получить две неупакованные BCD-цифры делимого. Это делает программист удобным для него способом. Далее нужно выдать команду aad – aad (ASCII Adjust for Division) – коррекция деления для представления в символьном виде.
Команда не имеет операндов и преобразует двузначное неупакованное BCD-число в регистре ах в двоичное число. Это двоичное число впоследствии будет играть роль делимого в операции деления. Кроме преобразования, команда aad помещает полученное двоичное число в регистр AL. Делимое, естественно, будет двоичным числом из диапазона 0… 99.
Алгоритм, по которому команда aad осуществляет это преобразование, состоит в следующем:
1) умножить старшую цифру исходного BCD-числа в ах (содержимое АН) на 10;
2) выполнить сложение АН + AL, результат которого (двоичное число) занести в AL;
3) обнулить содержимое АН.
Далее программисту нужно выдать обычную команду деления div для выполнения деления содержимого ах на одну BCD-цифру, находящуюся в байтовом регистре или байтовой ячейке памяти.
Аналогично ааш, команде aad можно найти и другое применение – использовать ее для перевода неупакованных BCD-чисел из диапазона 0… 99 в их двоичный эквивалент.
Для деления чисел большей разрядности, так же как и в случае умножения, нужно реализовывать свой алгоритм, например «в столбик», либо найти более оптимальный путь.
Арифметические действия над упакованными BCD-числами
Как уже отмечалось выше, упакованные BCD-числа можно только складывать и вычитать. Для выполнения других действий над ними их нужно дополнительно преобразовывать либо в неупакованный формат, либо в двоичное представление. Из-за того, что упакованные BCD-числа представляют не слишком большой интерес, мы их рассмотрим кратко.
Сложение упакованных BCD-чисел
Вначале разберемся с сутью проблемы и попытаемся сложить два двузначных упакованных BCD-числа. Пример Сложение упакованных BCD-чисел:
67 = 01100111
+
75 = 01110101
=
142 = 1101 1100 = 220
Как видим, в двоичном виде результат равен 1101 1100 (или 220 в десятичном представлении), что неверно. Это происходит по той причине, что микропроцессор не подозревает о существовании BCD-чисел и складывает их по правилам сложения двоичных чисел. На самом деле, результат в двоично-десятичном виде должен быть равен 0001 0100 0010 (или 142 в десятичном представлении).
Видно, что, как и для неупакованных BCD-чисел, для упакованных BCD-чисел существует потребность как-то корректировать результаты арифметических операций.
Микропроцессор предоставляет для этого команду daa – daa (Decimal Adjust for Addition) – коррекция результата сложения для представления в десятичном виде.
Команда daa преобразует содержимое регистра al в две упакованные десятичные цифры по алгоритму, приведенному в описании команды daa Получившаяся в результате сложения единица (если результат сложения больше 99) запоминается в флаге cf, тем самым учитывается перенос в старший разряд.
Вычитание упакованных BCD-чисел
Аналогично сложению, микропроцессор рассматривает упакованные BCD-числа как двоичные и, соответственно, выполняет вычитание BCD-чисел как двоичных.
Пример
Вычитание упакованных BCD-чисел.
Выполним вычитание 67–75. Так как микропроцессор выполняет вычитание способом сложения, то и мы последуем этому:
67 = 01100111
+
-75 = 10110101
=
-8 = 0001 1100 = 28
Как видим, результат равен 28 в десятичной системе счисления, что является абсурдом. В двоично-десятичном коде результат должен быть равен 0000 1000 (или 8 в десятичной системе счисления).
При программировании вычитания упакованных BCD-чисел программист, как и при вычитании неупакованных BCD-чисел, должен сам осуществлять контроль за знаком. Это делается с помощью флага CF, который фиксирует заем из старших разрядов.
Само вычитание BCD-чисел осуществляется простой командой вычитания sub или sbb. Коррекция результата осуществляется командой das – das (Decimal Adjust for Substraction) – коррекция результата вычитания для представления в десятичном виде.
Команда das преобразует содержимое регистра AL в две упакованные десятичные цифры по алгоритму, приведенному в описании команды das.
Данный текст является ознакомительным фрагментом.