Редактор Stimulus

Редактор Stimulus

В PSpice используются различные формы (stimuli) напряжений или токов. Формы напряжения, представляемые синусоидой, экспонентой, прямоугольными импульсами, кусочно-линейной функцией (PWL), квазигармоникой с модулируемой частотой, рассматривались в последнем разделе главы 4. Для краткого знакомства с методикой применения редактора Stimulus в Capture, рассмотрим источник синусоидального напряжения, который имеет эту форму

sin(<vo> <va> <f> <td> <df> <phase>),

где vo — напряжение смещения, va — амплитуда напряжения, f — частота, td — запаздывание, df — коэффициент затухания и phase — начальная фаза синусоидального сигнала. В PSpice команда ввода выглядит как

V 1 0 sin (0.3V 1V 500Hz 0 500 0)

Эта команда использовалась в примере главы 4 (см. полученный в результате график на рис. 4.30). С другой стороны, синусоидальный источник тока можно было бы ввести как

I 1 0 sin(0.2А 0.75А 60Hz 0 0 90)

Здесь первый параметр io — ток смещения, второй параметр ia — амплитуда тока, а остальные параметры не отличаются от приведенных в команде для источника напряжения.

Редактор Stimulus программы Capture разрешает пользователю просмотреть график заданного сигнала на экране до того, как он будет использован в схеме.

Это справедливо для всех форм напряжения, которые поддерживаются OrCAD PSpice. Однако редактор Stimulus демонстрационной версии можно использовать только для функции sin().

В качестве простого примера начнем новый проект с именем stimcase и вызовем компонент VSTIM из библиотеки SOURCSTM для формирования синусоидального напряжения. Вставьте в схему последовательную цепочку из R=1,5 Ом и L=5,3 мГн, как на рис. 2.1. Выберите свойства реализации источника напряжения (implementation) и назовите его Vsin. Затем выберите символ для формы и из главного меню выберите Edit, PSpice Stimulus. Появится окно Stimulus Editor. Если вы используете демонстрационную версию, то сможете устанавливать в этом окне атрибуты только для синусоидальной формы. Окно для установки атрибутов SIN() показано на рис. 17.1 и должно быть заполнено так, как в приведенном примере. Установите следующие значения: Offset value=2 В, Amplitude=1,5 В, Frequency(Hz)= 0 Гц, Time delay(с)=0, Damping factor(1/c)=0 и Phase angle(градусы)=90. После установки значений в окне предварительного просмотра появится диаграмма синусоидального напряжения. Оно должно иметь максимальное значение 3,5 В и минимальное 0,5 В, создавая значение двойной амплитуды 3 В (или амплитуду 1,5 В), постоянную составляющую, равную 2 В, и начальный фазовый угол 90°.

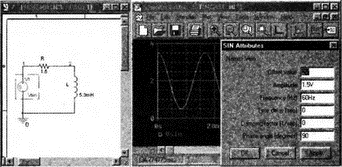
Рис. 17.1. Окно для установки атрибутов синусоидального сигнала

Когда вы нажмете OK, закрывая окно SIN Attribute, появится запрос, хотите ли вы сохранить изменения (ответьте «да») и модифицировать схемное решение (ответьте «да»). Подготовьте моделирование на PSpice, выбрав New Simulation Profile с именем Stimcas1 и выберите анализ переходных процессов во временной области для интервала в 40 мс с максимальным размером шага 40 мкс. Проведите моделирование и получите в Probe графики V(1), V(2) и I(R) на одном экране, как показано на рис. 17.2. В начале графика входное напряжение имеет значение 3,5 В, как и при предварительном просмотре формы. Другие кривые искажены из-за переходного процесса. Выберите момент, когда V(1) находится в максимуме при t=16,68 мс, затем найдите момент, когда в максимуме находится ток при t=19,143 мс. Отметьте, что ток отстает от приложенного напряжения на 2,463 мс, что соответствует 53,1°. Результаты не отличаются от полученных в соответствующем примере из главы 2.

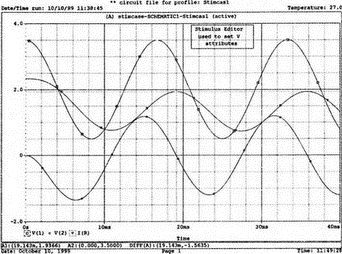
Рис. 17.2. Временные диаграммы, полученные с использованием Stimulus Editor

В качестве упражнения убедитесь, что ток имеет величину 0,6015 А, а напряжение на катушке индуктивности равно 1,1933 В. Отметим, что в представленном примере величина входного напряжения составляет 1,5 В, в то время как в первом примере из главы 2 оно было равно 1,0 В. 

**** 10/10/99 11:38:45 *********** Evaluation PSpice (Nov 1998) **************

** circuit file for profile: Stimcas1

**** CIRCUIT DESCRIPTION

*Libraries:

* Local Libraries :

.STMLIB ".STIMCASE.stl"

* From [PSPICE NETLIST] section of pspieeev.ini file:

.lib nom.lib

*Analysis directives:

.TRAN 0 40ms 0 40us

.PROBE

*Netlist File:

.INC "stimcase-SCHEMATIC1.net"

* Alias File:

**** INCLUDING stimcase-SCHEMATIC1.net ****

* source STIMCASE

L_L  2 0 5.3mH

R_R  1 2 1.5

V_V1 1 0 STIMULUS=Vsin

**** RESUMING stimcase-SCHEMATIC1-Stimcas1.sim.cir ****

.INC "stimcase-SCHEMATIC1.als"

**** INCUDING stimcase-SCHEMATIC1.als ****

.ALIASES

L_L  L(1=2 2=0 )

R_R  R(1=1 2=2 )

V_V1 V1(+=1 -=0 )

.ENDALIASES

**** RESUMING stimcase-SCHEMATIC1-Stimcas1.sim.cir ****

.END

* E:SPICESTIMCASE.stl written on Sun Oct 10 11:02:54 1999

* by Stimulus Editor -- Evaluation Version 9.0

;!Stimulus Get

;! Vsin Analog

;!Ok

;!Plot Axis_Settings

;!Xrange 0s 60ms

;!Yrange 0 4

;!AutoUniverse

;!XminRes 1ns

;!YminRes 1n

;!Ok

.STIMULUS Vsin SIN( 2V 1,5V 60Hz 0 0 90 )

**** INITIAL TRANSIENT SOLUTION TEMPERATURE = 27.000 DEG С

NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE

( 1) 3.5000  ( 2) 0.0000

VOLTAGE SOURCE CURRENTS

NAME  CURRENT

V_V1 -2.333E+00

TOTAL POWER DISSIPATION 8.17Е+00 WATTS

Рис. 17.3. Выходной файл для анализа с использованием Stimulus Editor

Выходной файл показан на рис. 17.3. Форма напряжения представляет собой синусоидальную зависимость (сдвинутую на 2 В по оси Y)

V_V1 1 0 STIMULUS=Vsin

.STIMULUS Vsin SIN( 2V 1.5V 60Hz 0 0 90 )

Выходной файл включает также ссылку на новую библиотеку STIMCASE.stl, созданную при использовании редактора Stimulus. Содержание этой библиотеки показано в выходном файле перед выводом решения для переходного процесса.

Мы заключаем, что проще использовать различные формы токов и напряжений в PSpice (как в главе 4), чем пытаться использовать единственную форму, доступную в Capture. В PSpice вышеупомянутая команда просто заменяется на

V 1 0 sin(2V 1.5V 60Hz 0 0 90)

Если вам необходимо применить источник тока или напряжения типов ехр(), pulse(), pwl(), sffm() или sin(), используйте методы, описанные в первых тринадцати главах этой книги.