Частотные зависимости полных проводимостей
Частотные зависимости полных проводимостей
Графическая методика, которая часто используется в схемотехническом анализе на переменном токе, основана на нахождении годографов полных сопротивлений или полных проводимостей. Если элементы включены последовательно, складываются частотные зависимости полных сопротивлений участков цепи и находится общая частотная зависимость. Если элементы включены параллельно, те же операции производятся для проводимостей отдельных ветвей.
Схема на рис. 2.23 содержит две параллельные ветви с параметрами: С=0,318 мкФ; RL=50 Ом и L=3,18 мГн. Во входном файле задан диапазон частот от 5 Гц до 10 кГц:
Locus of Admittances
V 1А 0 AC 1V
R 1 1A 1
RL 1 2 50
L 2 0 3.18mH
C 1 0 0.318 uF
.AC LIN 201 5Hz 10kHz
.PROBE
.END
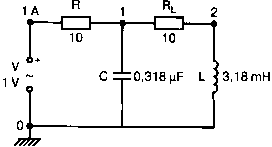
Рис. 2.23. Схема для определения фазовых траекторий проводимости
Выполните анализ и выведите график IP(R), чтобы найти резонансную частоту. Воспользовавшись курсором, убедитесь, что f0=4,336 кГц. Теперь измените шкалу по оси X так, чтобы это позволило представить полную проводимость во всем диапазоне. Поскольку V=1 В, Y=I/V=I/1. Таким образом, проводимость Y численно равна току, и вы можете заменять график I графиком Y и наоборот. Вы можете получить также зависимость B(G), где активная составляющая проводимости G откладывается по горизонтальной, а реактивная составляющая B — по вертикальной оси. Координаты точек такого графика представляют собой действительную и мнимую составляющие вектора проводимости, а совокупность точек служит годографом вектора проводимости при изменении частоты.
Прежде чем пытаться изменить масштаб по оси X, удалите кривые, имеющиеся на экране, и выберите Plot, Axis Settings…, опции Auto Range, Linear, затем нажмите кнопку Axis Variable. Для выбора функции введите с клавиатуры «IR(R)» и дважды щелкните OK. Затем получите график II(R). Поскольку I и Y численно равны, можно считать, что по осям отложены действительная G (ось X) и мнимая В (ось Y) составляющие, а весь график рассматривать как годограф проводимости (Y-plane). График содержит важную информацию, которая видна не сразу. Верхний левый конец кривой соответствует частоте f=10 кГц. При перемещении точки вниз вправо уменьшается частота, при которой могут быть получены соответствующие значения В и G. Переместив курсор в точку, где В=0 (примерно), вы увидите, что при этом G=5 мС. Вследствие этого полное сопротивление цепи при резонансной частоте 4,336 кГц равно 200 Ом.
Распечатайте годограф проводимости. Отметьте ось Х как G (в мС) и ось Y как В (также в мС) для дальнейшего изучения. Ваш график должен быть похож на график, приведенный на рис. 2.24.
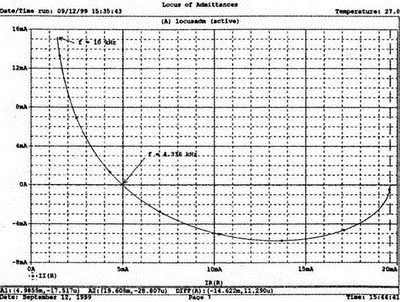
Рис. 2.24. Годограф полной проводимости для схемы на рис. 2.23
Вы знаете, где размещены на этом графике две частоты, но как вы можете идентифицировать другие? Простой метод состоит в том, чтобы изменить во входном файле верхнюю границу частоты в команде вариации частоты. Для начала установите ее равной 6 кГц и снова выполните моделирование. Получив значения карты проводимости, запомните, где начинается график (6 кГц), и отметьте эту точку на предыдущем графике, пользуясь значениями G и В. Сделайте это несколько раз для других значений верхней границы, отмечая каждое новое положение точки значением f на первоначальном графике.
Данный текст является ознакомительным фрагментом.