Модель нелинейных взаимодействий

При наличии нелинейности или проявлении ее при интенсивных воздействиях восприимчивость ? становится нелинейной функцией внешнего воздействия и тогда отклик системы: О = ?н В

Рассмотрим нелинейное преобразование различных воздействий физических полей. Результат воздействия на нелинейную среду Вi (t) соответствующих i воздействий (i = 1,2,3…n).

Пусть среда, область взаимодействия полей характеризуется амплитудной функцией преобразования выходного параметра, отклика О от входного воздействия В полиномом k—той степени, которая записывается (9.1).

На область взаимодействия поступает воздействие различных градаций параметров поля, которое характеризует воздействия суммы n излучений и определяется функцией (9.2). Результат нелинейного преобразования процесса В (t) запишется (9.3), где bk – определяет крутизну нелинейной функции взаимодействия. Представленную модель взаимодействия применяют для описания любых физических полей.

Для примера, рассмотрим взаимодействия полей (электромагнитных или гидроакустических) с амплитудной функцией нелинейности, которая характеризуется полиномом третей степени (k=3). Тогда характеристика поля (напряженность поля или уровень давления) при синусоидальном входном воздействии запишется так:

Ввх = В1 +В2 =В1соs?1+ В2 cos?2. В результате взаимодействия по расчету будем иметь основные частоты ?1, ?2, 2?1, 3?1, частоты от квадратичного члена полинома ?1 ± ?2, частоты от кубического члена 2?1- ?2; 2?2- ?1.

В общем случае возникают комбинационные колебания на частотах nfi ± k fi от квадратичных, кубичных и k-ых степеней полинома, описывающего воздействия. Натурные измерения, которые выполнялись автором в различные периоды на нелинейных средах и элементах для ЭМП, ЭП, ГАП, показали наличие комбинационных частот. Один из результатов приведен в /2/.

При воздействии на физическую систему различных полей важно учитывать состояния, поведения системы. В линейных системах имеется одно состояния равновесия. Если система нелинейная, то могут существовать несколько состояний равновесия. Устойчивое состояние сохраняется, неустойчивое не сохраняется. Имеются разные критерии состояния (Гурвица, Ляпунова и др.), когда физическая система описывается системой n-дифференциальных уравнений.

Часто применяют уравнение вида (9.4), где функция f (v, dv/dx) в общем случае является нелинейной, а е (х) представляет собой периодическую внешнюю силу; ? – безразмерное время; ?o – период внешней силы, воздействия.

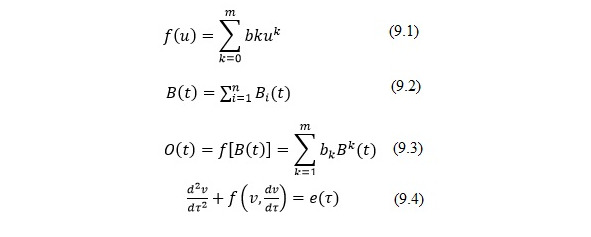
Важно, что в одной и той же нелинейной системы могут существовать различные виды периодических колебаний.

Рассмотрим характерные виды колебаний.

1. Случай гармонических колебаний, в которых основная составляющая преобладает над более высокими гармоническими колебаниями.

2. Если условия устойчивости нарушаются, то происходит аномальное возбуждение ультрагармоник на частотах f 1гор, f 2гор… f iгор.

3. Субгармонические колебания с основной частотой f iсуб.= f осн. (1/ n), где (n=2,3,4) возникают на нелинейностях и относятся к определенному типу нелинейных колебаний.

Приведенную модель можно использовать для основного класса взаимодействий физических полей.

Нелинейный эффект – это эффект, описываемый нелинейной зависимостью, нелинейным уравнением. Нелинейная теория – это теория, в основе которой лежат нелинейные связи между объектами. Совсем простое нелинейное уравнение может иметь бесчисленное множество решений. Множеству решений соответствует множество путей эволюции нелинейной системы и тогда эта система может пойти по одному или качественно иному пути развития.

Разные процессы в разных естественных науках (физики, химии, биологии и др.), а также в экономике, социологии, медицине, в технических приложениях описываются одинаковыми или сходными моделями. Эти модели предсказывают сходные конечные результаты.

В решении проблемы комплексной защиты объектов информатизации задачи защиты информации прежде всего следует рассматривать как изменение физических полей. Многообразие физических полей и особенно продуктов взаимодействия, например, таких как наличие большого класса излучений ставит задачу скрытия и изменения характеристик поля в задачах защиты информации. Требуется энергетические затраты и использование технических средств. Наличие широкого спектра частот с другой стороны говорит о «размазывании» сигнала в пространстве физического поля, что является показателем скрытности, большой базы сигнала. И тогда имеется путь повышения эффективности защиты в создании технических средств обработки информации с большой базой.