Суперпозиция акустических волн
В практике защиты информации мы будем иметь акустические и звуковые волны, которые распространяются в газообразных, жидких и твердых средах. Для жидкости и газа могут существовать только продольные волны, для которых направление колебаний частиц среды совпадают с направлением распространения волны. Эти волны мы будем сейчас рассматривать. Точнее рассмотрим плоскую волну, у которой фронт представляет собой плоскость
Если через некоторую точку среды проходит ряд гармонических волн, то колебания при малых амплитудах суммируются (принцип суперпозиции), т. е. результирующее колебание равно сумме колебаний, создаваемых отдельными волнами. Возникает явление интерференции волн. При интерференции гармонических волн амплитуда результирующего колебания определяется по следующему правилу: если складываются гармонические колебания одинаковой частоты, то вектор результирующего колебания является суммой векторов составляющих колебаний (рис. 5). Амплитуда и фаза результирующего колебания зависят, следовательно, от отношения между фазами слагаемых колебаний.
Рассмотрим основные соотношения, касающиеся интерференции волн. Пусть в некоторую точку С среды доходят гармонические колебания, распространяющиеся от двух источников 1 и 2 (рис. 6). Если считать, что фазы колебания источников одинаковы (синфазные источники), то сдвиг фаз ? колебаний, достигших точки С, зависит лишь от разности ? расстояний от источников до рассматриваемой точки или, иначе говоря, от разности хода лучей. Разность фаз ? определяется формулой (7.1) т. е. отношением разности хода лучей к длине волны.
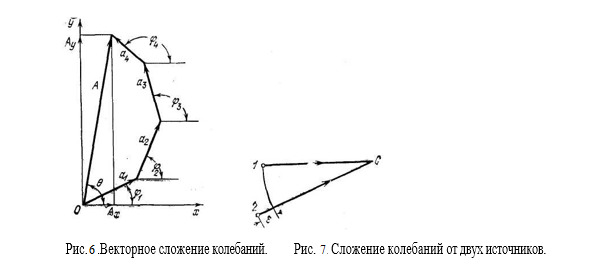
Если амплитуды слагаемых колебаний одинаковы и равны а, то, складывая векторы, соответствующие этим колебаниям (рис. 7), найдем величину А вектора результирующего колебания (7.2), где Ат=2а — максимальная амплитуда. Подставляя ? = 2л?/?,, получим (7.3).
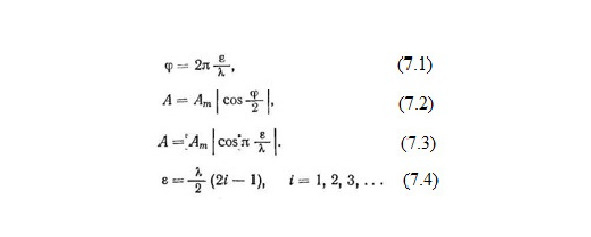
Рассматривая амплитуду результирующего колебания, мы всегда будем иметь в виду абсолютное значение величины А. Как видим, амплитуда результирующего колебания зависит от отношения разности хода к длине волны ?. Если разность хода лучей равна целому числу длин волн, то колебания складываются в фазе и амплитуда результирующего колебания равна удвоенной амплитуде слагаемых колебаний Если разность хода лучей равна нечетному числу полуволн, то колебания складываются в противоположных фазах и в результате получится ноль.
Таким образом, максимум Ат=2а будет при условии ?=? i, i=l, 2, 3, …, минимум A= 0 при (7.4).
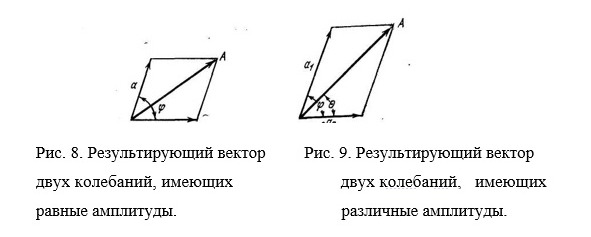
Накладываются две волны с неравными амплитудами а1 и а2 (рис.9)
Определяя амплитуду А результирующего колебания, получим (7.5). Максимальная амплитуда равна а1 + а2 при ?=? i. Минимальная амплитуда равна а1 – а2 при ?= ?/2 (2i-1).
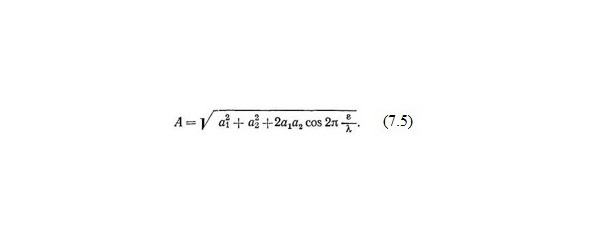
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.