Рассмотрим суперпозицию ЭМП-ЭМП и поляризацию

ЭМП рассматривали как волновой процесс, который описывается однородным уравнением Гельмгольца (6.1), где (6.2) – оператор Лапласа, (6.3) – волновое число или постоянная распространения, (6.4) – абсолютные диэлектрическая и магнитная проницаемости, (6.5) – относительные диэлектрическая и магнитная проницаемости.

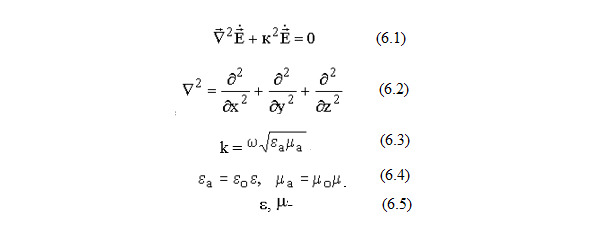
Рассмотрим плоскую электромагнитную волну. Это волновой процесс, у которого амплитуды электрической и магнитной составляющих поля во всех точках плоскости, перпендикулярной направлению распространения волны, имеют одинаковые значения.

Волновое уравнение для плоского поля является линейным дифференциальным уравнением, сумма нескольких его решений также будет являться решением этого уравнения. Таким образом, сложные типы электромагнитных волн можно представлять себе составленными из большого числа элементарных плоских волн с различными амплитудами, фазами и направлениями распространения. В большинстве практических задач, однако, эта точка зрения имеет лишь методическое значение; методы количественного анализа для таких задач будут рассмотрены ниже. Лишь в случае, когда элементарные плоские волны распространяются в одном и том же направлении, имеет смысл вместо суммарной волны рассматривать её элементарные составляющие и находить суммарные свойства путём суперпозиции свойств составляющих. Для таких сложных волн ориентация векторов поля описывается понятием поляризации волны (рис.5).

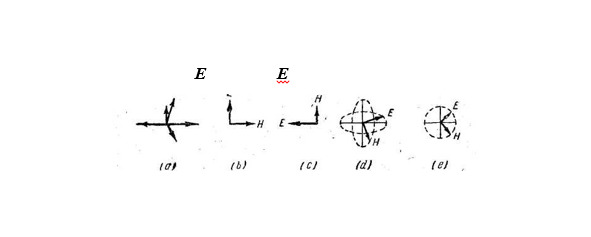
Рис. 5 – (а) Неполяризованная волна, (b) Вертикально поляризованная волна, (с) Горизонтально поляризованная волна, (d) Эллиптически поляризованная волна, (е) Волна, поляризованная по кругу.

Для элементарной плоской однородной волны векторы электрического и магнитного полей всегда взаимно перпендикулярны в любой точке пространства.

Сочетание элементарных волн, распространяющихся в одном направлении, при произвольной ориентации их векторов поля, называется неполяризованной волной. Её отдельные составляющие волны могут иметь также произвольные амплитуды и фазы [рис.].

Если векторы поля для всех элементарных волн, распространяющихся в одном направлении, сохраняют одно и то же общее направление, то суммарная волна называется плоскополяризованной. Здесь может возникнуть вопрос, относятся ли эти определения только к волнам одной и той же длины или нет. В радиотехнике чаще всего приходится иметь дело с волнами, распространяющимися в свободном пространстве, для которого постоянная распространения не зависит от частоты; поэтому вышеприведенные определения относятся к волнам любой длины. Тем не менее, в случае волны, составленной из двух элементарных волн различной длины и имеющих общее направление распространения и ориентацию векторов поля, мы предпочтительнее будем говорить не о суммарной волне, а о двух элементарных волнах с одинаковой поляризацией, но имеющих различную длину.

Плоскость поляризации обычно определяется в радиотехнике ориентацией вектора электрического поля, в противоположность оптике, где принято, что плоскость поляризации» совпадает с вектором магнитного поля. Таким образом, согласно радиотехнической терминологии, волны с вектором электрического поля, направленным вертикально, будут называться вертикально поляризованными. Волны с горизонтально направленным электрическим вектором будут называться горизонтально поляризованными [рис. (b) и (с)].

Сочетание двух однородных плоских волн, отличающихся по амплитуде, фазе и ориентации векторов поля, но имеющих одну и ту же длину, называется эллиптически поляризованной волной. Для того чтобы уяснить смысл этого термина, мы разложим каждую из элементарных волн на две одну с электрическим вектором, направленным вдоль оси х, и другую – вдоль оси у. Сложим теперь обе волны, имеющие электрический вектор в направлении x; в результате мы получим волну определённой амплитуды и фазы, которая запишется, если воспользоваться тригонометрическим выражением, в виде (6.6).

Две волны, имеющие электрический вектор в направлении у, дадут, в результате их сложения другую волну, отличную от первой по амплитуде и фазе (6.7).

Для некоторой плоскости, например z = 0, оба выражения упрощаются (6.8 – 6.9).

Это является уравнением эллипса в параметрической форме: конец вектора электрического поля вычерчивает в плоскости, перпендикулярной к направлению распространения, эллипс. Это обстоятельство и служит поводом для названия «эллиптическая поляризация» [рис. (d)].

Если исходные волны таковы, что составляющие по осям xи уравны по амплитуде и расходятся по фазе на 90°, эллипс вырождается в окружность, и волна обладает

круговой поляризацией. Действительно, если (6.10 – 6.11), что является уравнением окружности, рис.

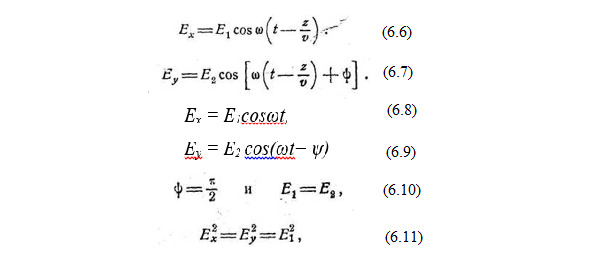
Линейные закономерности можно рассматривать как частный случай нелинейных.