Нормальное распределение
Форма кривых нормального распределения представлена ниже.
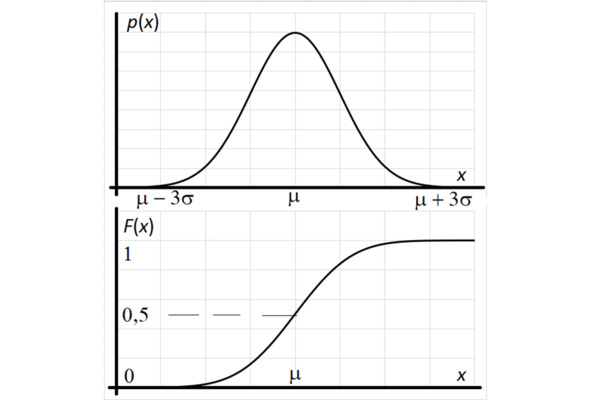
Нормальное распределение
Форму нормального распределения определяют два параметра:
µ – среднее значение (математическое ожидание);
? – стандартное отклонение.
График плотности вероятности p (x) симметричный относительно среднего значения. Кривая практически спадает до нуля при отклонении от среднего на три сигмы. Нарисуйте схематичное изображение кривой плотности вероятности, указав среднее и пределы изменения значений по оси х.
График кумуляты (накопленных частот) F (x) плавно возрастает. Кривая проходит через три ключевые точки – см. формулы.

Ключевые точки кумуляты
Конечно, это очень приближённое описание формы кривой. На самом деле, линия доходит до нуля и до единицы только при бесконечно больших и бесконечно малых значениях. Но нас сейчас интересует только общая картина.
Нарисуйте схематичное изображение функции распределения, указав среднее и пределы изменения значений по оси х – в соответствии со своим вариантом задания.
Пример зарисовки графиков распределения для нулевого варианта приведён ниже.
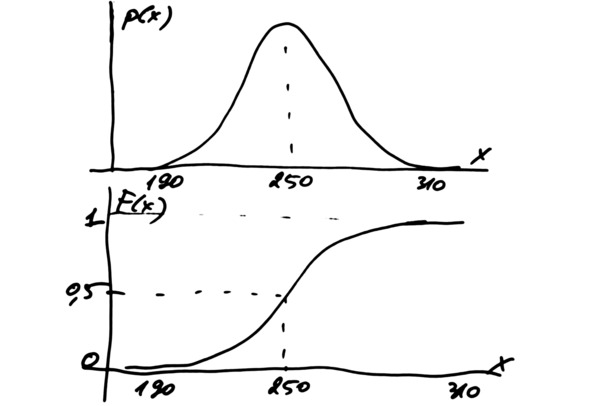
Зарисовка
Сделайте зарисовки формы распределения на бумажном листе от руки. Здесь не требуется искусство композиции или навык черчения. Достаточно схематичной зарисовки. В следующем разделе мы рассмотрим, как вставить зарисовку на лист Excel.
Характеристики нормального распределения определяются следующим образом – см. формулы.

Характеристики нормального распределения
Оцените характеристики распределения для своего варианта и укажите их на том же листе.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.