Антон Войтишек (ИВМиМГ СО РАН) о случайных и псевдослучайных числах Алла Аршинова
Антон Войтишек (ИВМиМГ СО РАН) о случайных и псевдослучайных числах
Алла Аршинова
Опубликовано 08 ноября 2010 года
В криптографии секретные коды представляют собой хаотические наборы (последовательности) нулей и единиц (это соответствует двоичному представлению целых чисел). Такое представление соответствует способу получения этих последовательностей. Берется некоторый «шумящий» прибор, который в данный момент времени может как выдать, так и не выдать определенный сигнал (в зависимости от результата в шифр заносится единица или нуль). Имеется довольно большое разнообразие таких приборов. Главные критерии их качества — быстрота фиксации и «непредсказуемость» наличия сигнала.
В частности, в октябрьском номере журнала Nature Photonics сообщается, что группа ученых из Германии и Дании создала квантовый генератор хаотических сигналов, который стал одним из лучших в мире по указанным критериям. Как пишет журнал «Успехи физических наук», принцип работы генератора основан на случайном характере вакуумных колебаний электромагнитного поля.
В литературе по криптографии хаотические последовательности нулей и единиц часто называют случайными числами. Понятие случайного (псевдослучайного) числа используется также в теории и приложениях численного статистического моделирования (или в методах Монте-Карло). Здесь случайные числа используются для имитации (моделирования) траекторий различных случайных процессов на компьютере с целью оценки требуемых усредненных характеристик этих процессов.
О том, в чем схожи и различны понятия и способы реализации случайного числа в криптографии и в вычислительной математике, рассказывает доктор физико-математических наук, ведущий научный сотрудник Института вычислительной математики и математической геофизики Сибирского отделения РАН, профессор кафедры вычислительной математики Новосибирского государственного университета, специалист в области теории методов Монте-Карло Антон Войтишек.
- Антон Вацлавович, чем различаются случайные и псевдослучайные числа в теории методов Монте-Карло? Как они соотносятся с понятием случайного числа в криптографии?
- При применении методов численного статистического моделирования требуется получать на компьютере выборочные значения случайных величин с различными законами распределения. Здесь используются различные формульные и алгоритмические преобразования стандартных случайных чисел ?j которые распределены равномерно в интервале (0,1) («на пальцах» это означает, что частота появления этих чисел в различных частях единичного интервала одинакова). А вот для получения чисел ?j используются датчики (генераторы) стандартных случайных чисел.
Различают физические датчики случайных чисел (основанные, кстати, на использовании упомянутых выше «шумящих» приборов) и генераторы псевдослучайных чисел (это специальные компьютерные программы, имеющие в языках программирования названия RAND или RANDOM).
Конструирование физических датчиков основано на том, что двоичное представление стандартного случайного числа ? (а именно такое представление чисел реализуется в компьютере) имеет вид
? = 0,10011001010...
то есть целая часть числа равна нулю (ведь ? расположено между нулем и единицей), а в «хвосте», следующем после запятой (этот «хвост» по научному называется мантиссой, а нули и единицы заполняют разряды мантиссы), стоят нули и единицы. Появление нуля и единицы (вне зависимости от значений в соседних разрядах) происходит с равной вероятностью (то есть с вероятностью 1/2).
Далее нужно сконструировать тот самый «шумящий» прибор, выдающий или не выдающий случайный сигнал в данный момент времени. Получение стандартных чисел ?j сведется к формированию соответствующих «хвостов» (мантисс) с помощью многократного обращения к прибору (наличие сигнала даст единицу в разряде мантиссы, отсутствие его даст нуль).
Определенная сложность состоит в том, что для применения методов Монте-Карло требуется прибор, позволяющий получать нули и единицы в разрядах мантиссы с равной вероятностью.
К слову, при получении чисел (шифров) в криптографии последнее требование желательно, но не обязательно. Здесь нет нужды увязывать наборы нулей и единиц с приведенным выше представлением стандартного числа ?j. Если обнаруживаются слишком длинные серии нулей или единиц, то реализуются специальные алгоритмы, удаляющие следы повторяемости. Это тоже обуславливает существенное отличие «криптографических» чисел от стандартных случайных чисел, используемых в методах Монте-Карло: для последних длинные серии нулей и единиц в мантиссе вполне допустимы.
- Какие сигналы можно использовать в физических датчиках?
- Можно крутить рулетку, раскрасив предварительно круг в два цвета (например, в красный и черный); красный цвет может соответствовать единице, черный — нулю. К слову, этот возможный способ получения стандартных случайных чисел обусловил название методов Монте-Карло, ведь в знаменитом игорном центре тоже крутят рулетку. Недостаток этого способа получения случайных чисел: долгое время реализации и отсутствие автоматизации процесса получения случайных нулей и единиц. Зато здесь более-менее гарантирована вероятность 1/2, если круг раскрашен двумя цветами пополам.
Автоматизация процесса формирования мантиссы стандартного случайного числа связана с применением различных случайных шумов. Иногда используются шумы самого компьютера. Более надежными и быстрыми считаются квантовые генераторы случайных шумов, в которых используются специальные свойства потоков малых (элементарных) частиц.
Проблему получения равных вероятностей появления нуля и единицы часто решают следующим образом. Сигнал замеряют дважды. Возможны следующие исходы: оба раза сигнал был (состояние СС), оба раза сигнала не было (состояние НН), первый был — второго не было (состояние СН) и первый не был — второй был (состояние НС). Если даже вероятность появления сигнала не равнялась в точности 1/2, то все равно состояния НС и СН являются равновероятными. То есть можно фиксировать только эти два состояния (приписав, например, состоянию НС единицу, а СН — нуль), а состояния СС и НН игнорировать.
Есть много ученых и практиков, убежденных в том, что только физические датчики могут дать «настоящие», «поистине случайные» наборы нулей и единиц. Ирония ситуации состоит в том, что уверенность этих исследователей часто зиждется на незнании природы того или иного шума (а вдруг он возникает благодаря каким-то вполне детерминированным — неслучайным — процессам?!).
Применение физических датчиков в расчетах по методу Монте-Карло имеет следующие трудности и недостатки. Во-первых, надежный датчик представляет собой недешевый прибор, в котором кроме всего прочего должны быть предусмотрены быстрые обмены информацией с компьютером. Во-вторых, требуется постоянная проверка выдаваемых датчиком последовательностей (здесь используется мощный аппарат критериев и методик математической статистики), так как даже сверхнадежное техническое устройство дает сбои. В-третьих, имеются отмеченные выше трудности получения равномерного распределения стандартного случайного числа.
Поэтому большинство расчетов по методу Монте-Карло производится с использованием генераторов псевдослучайных чисел.
- Как устроены генераторы псевдослучайных чисел?
- Большинство таких генераторов основаны на применении так называемого метода вычетов и его модификаций. Идея довольно проста. Берется дробное число ?i с большим «хвостом» (то есть с длинной мантиссой), умножается на большое целое число M, в результате получается большое целое плюс дробная часть. Потом целую часть результата убирают, а дробную берут в качестве следующего числа:
?i+1 = {M?i}
Оказывается, если множитель M взять достаточно большим (например, в современных генераторах используются множители порядка M = 5100109) получается, что «хвосты» ?i+1 ведут себя как настоящие стандартные случайные числа ?.
На самом деле «настоящее» (теоретическое) значение стандартного случайного числа получить невозможно, так как ? представляет собой дробь с бесконечной мантиссой, состоящей из нулей и единиц (такую дробь в принципе воспроизвести нельзя). Здесь ситуация похожа на проблему воспроизведения вещественных (в частности, иррациональных) чисел на компьютере.
На практике в методе вычетов при представлении чисел ?i берут «длинные» мантиссы (например, в современных генераторах используется T = 128 разрядов мантиссы).
В методе вычетов имеется также проблема периодичности: не позднее, чем через 2T шагов произойдет «зацикливание» генератора. В расчетах по методу Монте-Карло не рекомендуется использование более чем L/2 обращений к генератору; здесь L — длина периода, равная числу шагов метода вычетов, после которого начинается повторение последовательности ?i. При удачном подборе множителя M можно получить величину периода L = 2T — 2 (это едва ли не «рекордный» результат). Для T = 128 величина L/2 равна 2125, этого вполне хватает для широкого класса современных задач, решаемых с помощью численного статистического моделирования.
Решение проблем конечности мантиссы (периодичности) не гарантирует качества получаемых чисел ?i. Требуется проведение тестов, показывающих, что эти числа по свойствам близки к настоящим (теоретическим) стандартным случайным числам ? (тем, что имеют бесконечную мантиссу). Здесь используют широкий спектр критериев и методик математической статистики.
Тестом можно считать и любую задачу с известным ответом, решаемую методом Монте-Карло. В этом смысле процесс проверки генераторов псевдослучайных чисел неограничен. Более того, для любого генератора, основанного на методе вычетов, можно найти «тяжелую» задачу, с которой он «не справится» (то есть правильный ответ не получится). Для такой задачи придется проводить усовершенствование метода вычетов. В частности, можно увеличить длину контролируемой мантиссы T и множитель M.
Следует, однако, учитывать, что увеличение этих величин ведет к росту компьютерных затрат при обращении к подпрограммам типа RAND и RANDOM (если в этих подпрограммах «запаян» метод вычетов). Вообще следует отметить, что обращение к генератору случайных чисел — достаточно дорогостоящая компьютерная операция (по сравнению, например, с простым сложением или умножением чисел). Поэтому считается, что тот алгоритм метода Монте-Карло будет работать эффективнее (быстрее), который использует меньше обращений к генератору псевдослучайных чисел.
- А какие задачи решаются методом Монте-Карло?
- В пятидесятые годы XX столетия расцвет метода Монте-Карло был связан с разработкой проблемы защиты ядерных реакторов. Прежде чем конструировать системы защиты от излучения «в железе», проводились компьютерные расчеты на основе математической модели процесса, схематично выглядевшей следующим образом.
Излучение трактовалось как поток малых частиц («фотонов»), пролетающих сквозь слой защиты, в котором хаотично расположены крупные частицы. «Фотон», сталкиваясь с крупной частицей, либо захватывается ею («поглощается»), либо рассеивается по некоторому вероятностному закону. Можно проследить (реализовав на компьютере) траектории фотонов и подсчитать, какая доля фотонов поглощается в слое защиты. Если эта доля близка к единице, то защита может считаться хорошей.
При реализации траектории «фотона» до поглощения нужны выборочные значения случайных величин с различными законами распределения. Для получения таких значений используют преобразования стандартных случайных чисел ?j.
Далее выяснилось, что с описанным случайным процессом движения «фотонов» можно соотнести определенное уравнение (интегральное уравнение Фредгольма второго рода), на основе которого можно строить так называемые весовые оценки для вычисления требуемых характеристик (функционалов) физического процесса. Введение весов позволяет в ряде случаев упростить компьютерную реализацию траекторий «фотонов».
Вычисляемые в данной задаче характеристики (функционалы) можно также трактовать как сумму интегралов бесконечной кратности.
Вообще в литературе метод Монте-Карло обычно представляется как специальный способ вычисления многократных интегралов. Часто для иллюстрации рисуют такую картинку.
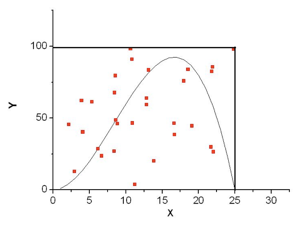
Численное интегрирование функции методом Монте-Карло (график из «Википедии»)
Предположим, нам нужно вычислить интеграл, равный площади S под кривой, изображенной на рисунке. Для этого поместим ее в прямоугольник с известной площадью U, и будем кидать в него равномерно распределенные случайные точки. Понятно, что вероятность P попадания случайной точки в интересующую нас область равна отношению площади этой области к площади прямоугольника: P = S/U. Реализуем большое количество точек N, и подсчитаем, какое количество точек K попадет под кривую. Частота K/N попадания случайных точек под кривую приближает вероятность P, и поэтому S/U ? K/N, а искомый интеграл приближенно равен S ? KU/N.
На самом деле даже в этом простейшем одномерном случае можно строить более «хитрые» весовые оценки интеграла S, позволяющие получить требуемый уровень погрешности приближения интеграла с меньшими затратами (в первую очередь — с меньшим количеством реализуемых случайных точек).
Одним из главных недостатков метода Монте-Карло является относительно медленное убывание погрешности приближения требуемой величины с ростом числа n реализаций случайных траекторий (точек). Эта погрешность убывает со скоростью n-1/2. То есть для уменьшения погрешности в десять раз требуется взять в среднем в 100 раз больше траекторий (точек). Поэтому многие сложные прикладные задачи решаются долго — иногда сутками (даже на современных суперкомпьютерах).
Для ряда «простых» задач (например, для задачи вычисления интеграла малой кратности с «хорошей», гладкой подынтегральной функцией) метод Монте-Карло проигрывает по эффективности детерминированным (как правило, сеточным) вычислительным методам.
Однако для большого класса весьма актуальных задач, связанных с вычислением многократных (даже бесконечнократных) интегралов или функционалов от решений интегральных уравнений и включающих негладкие входные данные, метод Монте-Карло практически не имеет конкурентов.
Можно также отметить, что методы Монте-Карло стремительно расширяют сферу применения. Эффективные алгоритмы численного статистического моделирования разработаны в физической и химической кинетике, статистической физике, теории массового обслуживания, финансовой математике, теории турбулентности, математической биологии и других областях.
В заключение отмечу, что бурное развитие школы методов Монте-Карло в новосибирском Академгородке на протяжении сорока с лишним лет связано с именем моего учителя, члена-корреспондента РАН Геннадия Алексеевича Михайлова. Под его руководством процветает большой отдел в Институте вычислительной математики и математической геофизики СО РАН, сотрудники которого успешно занимаются вопросами теории и приложений методов Монте-Карло.
К оглавлению
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
О случайных числах и сеансовых ключах
О случайных числах и сеансовых ключах Для генерации одноразовых симметричных сеансовых ключей PGP использует криптографически стойкий генератор псевдослучайных чисел (ГПСЧ)[11]. Если файл ПСЧ отсутствует, он автоматически создаётся и заполняется абсолютно произвольными
Александр Бондарь (ИЯФ СО РАН) о megascience-проектах Алла Аршинова
Александр Бондарь (ИЯФ СО РАН) о megascience-проектах Алла Аршинова Опубликовано 20 сентября 2011 года Этим летом Министерство образования и науки РФ выбрало шесть научных установок, претендующих на государственную поддержку в финансировании. Все они
Александр Лазуткин о перспективах космонавтики Алла Аршинова
Александр Лазуткин о перспективах космонавтики Алла Аршинова Опубликовано 11 января 2012 года - Александр Иванович, чем вы занимались на станции «Мир», в каких участвовали экспериментах? - Я был бортинженером. В обязанность бортинженеров
Сергей Таскаев (ИЯФ) о бор-нейтронозахватной терапии Алла Аршинова
Сергей Таскаев (ИЯФ) о бор-нейтронозахватной терапии Алла Аршинова Опубликовано 18 мая 2010 года Бор-нейтронозахватная терапия — это способ избирательного поражения клеток злокачественных опухолей. Физический принцип терапии прост: в кровь
Сергей Перминов (СО РАН) о невидимости Алла Аршинова
Сергей Перминов (СО РАН) о невидимости Алла Аршинова Опубликовано 19 августа 2010 года Шапка-невидимка, как показывает реальность — это очень привлекательный сюжет не только для художественной литературы и кинематографа, но и для научных разработок.
Вадим Яковлев (ИК СО РАН) о перспективах биотоплива Алла Аршинова
Вадим Яковлев (ИК СО РАН) о перспективах биотоплива Алла Аршинова Опубликовано 22 декабря 2010 года Практически все виды топлива, особенно на основе нефти, сложно и дорого производить. Сторонники альтернативной энергетики предлагают в качестве
Космический лифт и космические сложности Алла Аршинова
Космический лифт и космические сложности Алла Аршинова Опубликовано 13 апреля 2011 года Традиционный способ доставки грузов на орбиту очень дорог. Например, перевозка одного килограмма на шаттле, по оценке НАСА, стоит примерно 22 тысячи долларов. На
Алексей Беклемишев (ИЯФ СО РАН) о термояде Алла Аршинова
Алексей Беклемишев (ИЯФ СО РАН) о термояде Алла Аршинова Опубликовано 14 апреля 2011 года Старший научный сотрудник Института ядерной физики им. Г.И. Будкера СО РАН, кандидат физико-математических наук Алексей Беклемишев рассказывает о проекте новой
Александр Симонов (СО РАН) о топливных элементах Алла Аршинова
Александр Симонов (СО РАН) о топливных элементах Алла Аршинова Опубликовано 27 июля 2011 года На проект «Новые электрокатализаторы на основе палладия для высокоэффективных и экологичных источников энергии» Александр Симонов с коллегами получил
Алла Аршинова Беседы о современной физике
Алла Аршинова Беседы о современной физике Запуск LHC (Large Hadron Collider — Большого адронного коллайдера, самого высокоэнергетичного ускорителя в истории) стал одним из наиболее масштабных событий в мире науки за последнее время. Долгий подготовительный этап завершен, поломка
Анатолий Богуславский о радиоактивных отходах Алла Аршинова
Анатолий Богуславский о радиоактивных отходах Алла Аршинова Опубликовано 09 ноября 2010 года Что делать с радиоактивными отходами (РАО) и отработанным ядерным топливом (ОЯТ)? Этим вопросом уже не первый десяток лет задаются ученые и политики. Есть
Дмитрий Вибе (ИА РАН) об астрофизических измерениях Алла Аршинова
Дмитрий Вибе (ИА РАН) об астрофизических измерениях Алла Аршинова Опубликовано 29 ноября 2010 года Научное знание копится веками. В стремлении постичь мир ученые строят гипотезы и теории, проектируют и воплощают в жизнь сложнейшие научные установки.
Астрофизик Сергей Попов о гравитационных волнах Алла Аршинова
Астрофизик Сергей Попов о гравитационных волнах Алла Аршинова Опубликовано 02 декабря 2010 года Общая теория относительности – одна из самых проверенных и надежных теорий в современной физике. Почти все предсказания в рамках этой теории были
Александр Бондарь (РАН) о «маленьких» коллайдерах Алла Аршинова
Александр Бондарь (РАН) о «маленьких» коллайдерах Алла Аршинова Опубликовано 07 октября 2010 года Физика высоких энергий известна неспециалистам в основном в связи с запуском проекта LHC (Large Hadron Collider, Большой адронный коллайдер). Из-за огромной
Валерий Тельнов (ИЯФ СО РАН) о бозоне Хиггса Алла Аршинова
Валерий Тельнов (ИЯФ СО РАН) о бозоне Хиггса Алла Аршинова Опубликовано 30 ноября 2012 года - Что такое бозон Хиггса? Зачем его придумали и так долго искали? - Все знают, что тела и элементарные частицы имеют массы. А как возникают массы? Казалось бы, что
"Возможно, следующий Google родится в России" Алла Аршинова
"Возможно, следующий Google родится в России" Алла Аршинова О «перезагрузке» отношений между Россией и США говорят уже давно. Подводя итоги прошлогоднего визита в Россию госсекретаря США Хилари Клинтон, посол США в Москве Джон Байерли заявил, что Россия и США идут к "новому