1.3. Системы счисления

1.3. Системы счисления

Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Существуют системы позиционные и непозиционные.

В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.

Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание можно принять любое натуральное число – два, три, четыре, шестнадцать и т. д. Следовательно, возможно бесконечное множество позиционных систем.

Десятичная система счисления

Пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, однако информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т. д. Самая правая цифра числа показывает число единиц, вторая справа – число десятков, следующая – число сотен и т. д.

Двоичная система счисления

В этой системе всего две цифры – 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Самая правая цифра числа показывает число единиц, следующая цифра – число двоек, следующая – число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число – представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.

Восьмеричная система счисления

В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает, как и в десятичном числе, просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем – 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.

Шестнадцатеричная система счисления

Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем – 16 (десятичное), в следующем – 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.

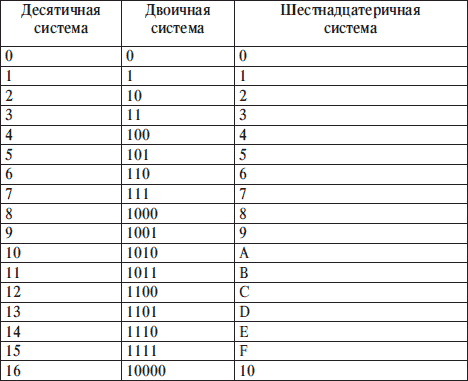
Таблица 1. Соответствие между первыми несколькими натуральными числами всех трех систем счисления