НАУКА: Мерцающий компьютер бесконечности
НАУКА: Мерцающий компьютер бесконечности
Автор: Леонид Левкович-Маслюк
Бесконечность – дело тонкое, и всякие вольности в обращении с ней выглядят крайне вульгарно. Беда в том, что в математике, особенно в той, что нужна инженерам и естественнонаучникам, вы натыкаетесь на бесконечность на каждом шагу. Чтобы вывести (или хотя бы осмысленно применять) формулы для расчета окружающих нас строений, устройств, механизмов, нужно владеть предельными переходами, решать дифференциальные уравнения, вычислять интегралы, суммировать ряды. Матанализ, первейший инструмент инженера-практика, прочно и глубоко связан с абстрактным и труднопостижимым понятием бесконечности, а уж почему так получилось – этот вопрос лучше адресовать куда-нибудь повыше.
Конечно, в прикладных разделах математики (да и в большинстве теоретических) бесконечность в мистически-пафосном смысле этого слова уже давно и тщательно заметена под ковер. Лучшие умы математики к середине-концу XIX века в основном придали математическому анализу его современную форму, где в рассуждениях и вычислениях фигурируют только конечные величины вместо понятных лишь гениям вроде Ньютона "моментов флюксий". Тем не менее бесконечность как концепция никуда не девается, она таится где-то в глубине, как кащеева игла, и вокруг нее витают темные флюиды логических туманностей и парадоксов, иногда очень эффектных – чего стоит хотя бы знаменитый парадокс Банаха-Тарского (см. стр. 26). Эти туманности, некогда привлекавшие широкое внимание, по-прежнему исследуют энтузиасты – но надо признать, что мода на разработку предмета с гордым названием "основания математики" прошла. Сегодня мало кто верит, что именно на этом пути, истоптанном титанами прошлого, найдется что-нибудь такое, что поможет радикально улучшить математику не в части логического обоснования, а в части прикладных результатов, – другими словами, поможет разработать новый математический язык, позволяющий выразить нечто совершенно новое об, извините за высокий слог, устройстве мира. Впрочем, за эксперименты с бесконечностью охотно берутся увлеченные непрофессионалы; часто – увлеченные катастрофически и безвозвратно. Увы, их писания обычно непригодны для таких журналов, как наш, столь же болезненно увлеченных идеей искать везде и всюду зерна рациональности или хотя бы вменяемости.
Работу математика Ярослава Сергеева, о которой мы сегодня рассказываем, нельзя отнести ни к одному из этих направлений мысли. От первого из них она отличается наглядностью и практической (по замыслу, по крайней мере) ориентированностью, от второго – полным соответствием научным стандартам. Сергеев воплотил в жизнь мечту, часто посещающую школьников и математиков-первокурсников, – придумал арифметику, объединяющую конечные и бесконечные числа. Более того, он разработал (и запатентовал!) конструкцию компьютера, выполняющего операции этой арифметики.
Рецензенты работ Сергеева предрекают, что на основе его результатов будет создано "множество новых мощных инструментов в анализе, информатике, теории множеств, теории измерений". Вполне возможно, что так и произойдет, но нельзя забывать, что такие прогнозы – дело очень неблагодарное. Энтузиазм по поводу перспектив нестандартного анализа – аппарата, созданного в 1960-е годы для введения в матанализ бесконечно малых и бесконечно больших чисел (см. врезку "Реинкарнация грифонов"), – был велик. Сегодня нестандартный анализ жив, но великих надежд с ним уже не связывают.
Реинкарнация грифонов
Вышедшая в 1987 году книга Владимира Успенского "Введение в нестандартный анализ" начиналась с вопроса: "Относятся ли грифоны и единороги к позвоночным?", который иллюстрировал экзотичность темы. В то время слово «грифон» было редким, индустрия фэнтези еще не вышла на книжный рынок, да и самого книжного рынка в России еще не было, да и сама Россия была еще Советским Союзом. Все с тех пор изменилось, а вот арифметика бесконечностей осталась экзотическим предметом – несмотря на то, что нестандартный анализ разрабатывался рядом крупных математиков начиная с 1960-х годов и популярность его была довольно высока.
Нестандартный анализ основан на системе "гипердействительных чисел", содержащей бесконечно малые и бесконечно большие величины и допускающей использование необходимых в анализе функций и эффективное решение уравнений. Построение гипердействительных чисел основано на сложной классификации бесконечных последовательностей обычных действительных чисел. При помощи этого аппарата были решены несколько серьезных задач функционального анализа, его использовали для описания «мгновенных» перестроек структуры решений дифференциальных уравнений. Сейчас "нестандартные методы" проникли в комплексный анализ, теорию чисел, алгебраическую геометрию, даже в некоммутативную геометрию, самый модный и стремительно развивающийся раздел современной математики. Впрочем, создатель некоммутативной геометрии Ален Конн (Alain Connes) высказывался о нестандартном анализе довольно резко. Причина (которую не отрицают, похоже, и энтузиасты нестандартной математики) – практически все, что удалось сделать с помощью этого аппарата, можно сделать и без него. Судя по обзору И. Фесенко (www.maths.nott.ac.uk/personal/ibf/rem.pdf), нестандартные методы сегодня рассматриваются скорее как "путеводная звезда" при поиске новых подходов к задачам.
Ниже мы расскажем об одном из первых приложений "бесконечных чисел" Сергеева – вычислении с их помощью геометрических характеристик фракталов, как классических, так и более общих, мерцающих (blinking fractals). Но прежде давайте разберемся в конструкции новой числовой системы.
?+1>?
Поясняя мотивы для разработки своей системы, Сергеев приводит пример арифметики, используемой одним из живущих в дельте Амазонки племен. Индейцы племени Пираха (Pirahг) считают так: один, два, много. Для них и 1 + 2 = много, и 2 + 2 = много. Что такое 3 или 4, они не представляют. Сергеев уверен, что этот примитивный способ счета очень важен для нас, потому что дает отличную аналогию с современным понятием бесконечности. Действительно, в системе счета Пираха операции много + 1 и много + 2 дают один и тот же результат: много. Нечто похожее мы имеем и в современной математике: ? + 1 = ? и ? + 2 = ?. Это сравнение наводит на следующую простую мысль: как индейцы Пираха не могут различить числа 3, 4, 5 и т. д. из-за неразвитости их системы записи конечных чисел, так и мы не можем различить бесконечные числа из-за неразвитости наших способов представления бесконечности. Именно поэтому возникают проблемы при вычислениях, связанных с бесконечно большими и бесконечно малыми величинами: невозможность их представления в памяти компьютера, необходимость введения понятия предела, неопределенные формы типа ? – ? и т. д., заключает Сергеев.
В основе конструкции Сергеева, призванной исправить дело, лежит гросс-единица (grossone), обозначаемая

Гросс-единица – это бесконечное число, равное по определению количеству элементов в множестве N натуральных (то есть целых положительных) чисел. Это определение надо понимать в дословном, буквальном смысле, то есть предполагать, что N имеет вид: {1, 2, 3, …,

– 1,

}. Другими словами,

– это "самое большое натуральное число". Оно и выбирается в качестве основания новой системы исчисления. Ну а дальше – точно так же, как мы записываем числа в десятичной системе, а компьютер в двоичной, произвольные бесконечно малые и бесконечно большие числа представляют собой «записи» (records) вида:
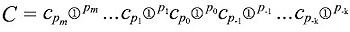
(1)
В этой записи p – «гросстепени», а c – «гроссцифры». Отличие от десятичной или двоичной систем в том, что «гроссцифры» не фиксированные заранее, а произвольные «обыкновенные» числа, записываемые с помощью конечного числа знаков. «Гросстепени», в свою очередь, это либо записи вида (1), либо снова «обыкновенные» конечные числа. Таким образом, числа в форме (1) всегда представляются конечным числом символов. Конечность записи принципиальна для этой конструкции, подчеркивает Сергеев, – она призвана учесть тот факт, что и человек, и компьютер способны выполнить лишь конечное число операций. В этом, кстати, существенное отличие от нестандартного анализа, который дополняет бесконечностями обычное множество вещественных чисел, построенное с помощью бесконечных десятичных дробей (или эквивалентных конструкций).
Сергеев с самого начала оставляет за скобками своих построений понятия счетного и несчетного множеств, взаимно однозначные соответствия и тому подобные базовые концепции привычной канторовской теории множеств. В его числовой системе, опять-таки в прямом и буквальном смысле слова, соблюдается древний постулат "часть всегда меньше целого". Например, число

+ 1 строго больше числа

, а множество натуральных чисел можно расширить так:
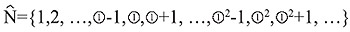
Записи вида (1) позволяют очень аккуратно сравнивать "маленькие бесконечности". Например, в обычной теории множеств совокупность всех натуральных чисел и совокупность четных положительных чисел неразличимы по так называемой мощности, и то и другое – счетные множества. Здесь же постулируется, что второе из этих множеств содержит ровно

/2 элементов, то есть вдвое меньше, чем первое. Аналогично, множество всех положительных чисел вида, например, (6К+3) будет состоять из (

/6) элементов; а если к нему добавить еще три числа другого вида, полученное множество будет состоять уже из (

/6 + 3) элементов.
1/

– простейшее по записи бесконечно малое ("инфинитезимальное") число. Арифметика записей (1) устроена самым естественным образом – они перемножаются и складываются так, как если бы вместо

стояло обыкновенное число. Тонкости начинаются при суммировании бесконечных рядов. Согласно одному из самых интересных постулатов теории Сергеева, любой процесс (в том числе и процесс суммирования ряда) может включать не более чем

шагов. В частности, параллельные процессы в этой модели принципиально более мощны, чем одиночные, последовательные, – ведь К параллельно идущих процессов позволяют выполнить (К*

) шагов. В этом же постулате о процессах скрыта и очевидная связь рассматриваемой модели с аксиомой выбора – источником множества трудностей и, в частности, «виновницей» парадокса Банаха-Тарского. Можно осторожно предположить, что настоящие теоретические трудности в согласовании концепций Сергеева с остальной математикой относятся именно к этим вопросам – но мы в них углубляться, разумеется, не будем. Во всяком случае, парадокс Банаха-Тарского в теории Сергеева не возникает – дело в том, что точки, из которых состоят шары, в данном случае можно просто пересчитать, выразив их количество соответствующей записью вида (1), и это не позволяет выполнять трюки с производством предметов из ничего.
Чуть позже мы приведем примеры прямого подсчета точек во фрактальных объектах, а пока черкнем еще пару формул. В любое выражение мы теперь можем подставлять не только конечные, но и бесконечные числа – и приписать вполне определенные значения как "стремящимся к бесконечности" в традиционном смысле слова рядам и функциям, так и рядам, которые вообще не имеют традиционного предела. Например, предел
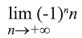
как известно, не существует. Однако с помощью записей (1) можно точно выразить значение этой последовательности в любой бесконечной точке: при n=

получаем

, при n=

– 1 получаем —

+1 и т. д.
Но содержат ли такие записи в новой арифметике действительно новую информацию о классических выражениях? Очень важный вопрос. Ответ на него даст только предстоящая история развития этого аппарата. Впрочем, уже существуют примеры описания наглядных геометрических конструкций – фрактальных процессов – при помощи новой числовой системы.
Отсчет мерцающих квадратиков
В известном фильме Питера Гринуэя "Отсчет утопленников" ("Drowning by numbers") персонажи монотонно и без особых хлопот применяют друг к другу одну и ту же элементарную операцию – утопление. По духу это очень напоминает классические конструкции фракталов – геометрических объектов, ставших популярными в последние десятилетия в самых разных областях науки и практики. Строгое математическое определение фракталов очень скучное, а интересны они тем, что чаще всего обладают свойством самоподобия: состоят из небольшого числа частей, каждая из которых – уменьшенная и слегка измененная копия объекта в целом. Самоподобие же почему-то встречается во всевозможных структурах нашего лучшего из миров – причем именно в таких, которые трудно описать гладкими функциями классического анализа. Например, фрактальный лист папоротника (рис. справа внизу) очень похож на настоящий. Задать такую форму можно либо с помощью длиннейших (но совершенно неинформативных в данном случае) рядов по синусам и косинусам, либо с помощью очень простого фрактального процесса, в явном виде учитывающего самоподобие этого листочка (а он состоит из трех уменьшенных копий самого себя: двух нижних веточек и того, что останется, если их отрезать). Папоротник тут не случаен – фрактальные модели (так называемые L-системы) построены для множества видов растений. Классик науки о фракталах Бенуа Мандельброт (если не ошибаюсь, он и ввел термин "фрактал") в начале 1960-х обнаружил фрактальные (в усредненном, статистическом смысле) структуры не где-нибудь, а в финансовых рядах – графиках колебания цен на рынках. Фрактальный характер имеет и множество других заманчивых объектов и процессов, включая строение Интернета и динамику сетевого трафика, и фрактальные компьютерные модели всего этого разрабатываются весьма активно. Проблема только в том, что построить такую модель для конкретного предмета из реального мира всегда крайне сложно. С формами растений это в целом удалось, а вот с финансовыми рядами – как-то пока не очень (хотя кто знает? может быть, нам не все рассказывают?).
Сами же фрактальные модели обычно представляют собой процессы последовательного измельчения и перемешивания исходных заготовок в соответствии с коротким списком правил. Как раз для точного подсчета (или отсчета?) того, что еще осталось от исходной заготовки после бесконечного числа таких шагов, Сергеев и использовал свои новые числа – в качестве иллюстрации их потенциальных возможностей.

Пример простого фрактального процесса – построение классического канторова множества. Заготовка – отрезок [0, 1]. Первый шаг – выбрасываем (Гринуэй, может быть, сказал бы – топим) среднюю треть этой заготовки. Получаем уже два отрезка, но маленьких: [0, 1/3] и [2/3, 1]. Затем топим (пардон, стираем) среднюю треть у каждого из этих двух, затем – у каждого из полученных четырех, и так далее. Ясно, что при рисовании на мониторе оставшиеся отрезки скоро станут меньше пикселов, и ничего кроме пустого экрана этот фрактальный процесс не даст (зато при другом выборе заготовок и операций с ними мы могли бы получить ветку сирени или реалистичный горный ландшафт).
Однако с точки зрения чистой математики в пределе остается отнюдь не пустота. Предельное канторово множество – трудновообразимый континуум (то есть нечто эквивалентное исходному отрезку!), все связи между точками которого разорваны выбрасыванием бесчисленных крошечных отрезков.
С использованием разложения по гросс-единицам Сергеев описывает этот процесс (и его результат) иначе. На n-м шаге процесса имеется 2n отрезков, каждый длиной 3-n. Стало быть, после

шагов бесконечно большое количество отрезков будет равно (2

), а их общая длина выразится бесконечно малым числом ((2/3)

). Эти выражения – точная характеристика фрактального множества, которая изменится при других параметрах порождающего процесса (если топить больше, или меньше, да еще и в других местах). Разумеется, аналогичные характеристики есть и в классике – например, фрактальная размерность, которая в данном случае равна log(2)/log(3). Но в классике лишен, конечно, смысла вопрос, насколько отличаются результаты последней и предпоследней из некоторого бесконечного числа итераций. Через новые числа это легко выразить: так, на шаге

– 1 общая длина отрезков равна (2/3) (

– 1).
Однако в новой системе невозможно пересчитать все полученные отрезки: ведь их будет (2

), то есть строго больше, чем

А мы помним постулат, что любой процесс, в том числе и процесс последовательного счета, не может использовать более

шагов. Зато здесь можно точно подсчитать число точек (!) в множестве, полученном после бесконечного числа шагов. Дело в том, что само понятие точки теперь сильно отличается от классического. "Как только мы выбрали символы для записи чисел, выражающих координаты точек, – поясняет Ярослав Сергеев, – мы определили понятие «точка» и можем легко сосчитать число этих точек. Более мощная система записи (например, система (1)) позволит нам увидеть больше точек, а более слабая (традиционная) – меньше".
Обратимся, наконец, к давно обещанным мерцающим фракталам. Мерцание заключается в том, что фрактальный процесс генерирует не одно, а несколько множеств. В данном случае их два, а процесс задан схемой:

Начав с синего квадрата, получаем на последовательных шагах такую динамику двух зависимых друг от друга множеств (см. схему внизу).
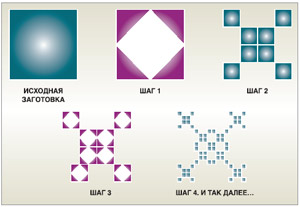
На четных шагах мы видим фигуру из синих квадратов, на нечетных – другую, составленную из красных треугольников. Описание динамики этого процесса в новой арифметике состоит в подсчете площади каждой фигуры на любом из шагов в процессе ее построения. Например, возьмем шаг

/2 – это четное бесконечное число, поэтому фигура в этот момент состоит из 2(3

/4) синих квадратов с общей бесконечно малой площадью 2(-

/4). На следующем шаге номер (

/2)+1 площадь фигуры из красных треугольников будет равна 2-

/4+1, и т. д. Вот так бесконечные числа описывают динамику этого мерцающего процесса – казалось бы, не имеющего предела в классическом смысле, подобно ряду 1, -1, 1, -1, …, 1. [Впрочем, аналогия тут не совсем полная.]
В заключение – скриншот "калькулятора бесконечности", построенного на основе уже работающего софтверного симулятора "компьютера бесконечности". Может быть, когда-нибудь мы увидим "компьютер бесконечности", реализованный в железе. Но это зависит от того, станет ли новая арифметика бесконечных чисел незаменимым инструментом решения сложных задач.
Ну а совсем в заключение – просим не рассматривать эту публикацию как сигнал о нашей особой заинтересованности в сочинениях именно на такие, фундаментальные и в то же время экзотические темы. Впрочем, независимо от тематики, мы пишем только о том, что прошло апробацию в солидной научной периодике, на серьезных конференциях и семинарах. Увлекательная работа Ярослава Сергеева именно такова.
Cправка

Ярослав Серегеев занимает должность "полного профессора", учрежденную в Университете Калабрии (Италия) для приглашения выдающихся ученых. Он также профессор Нижегородского государственного университета им. Н. И. Лобачевского, доктор физико-математических наук, специалист по численному анализу, параллельным вычислениям, глобальной оптимизации, автор более 150 научных публикаций, среди которых 50 статей в международных журналах и три книги. Сергеев – один из организаторов и координатор Российско-Итальянского университета, действующего при Нижегородском университете.
Арифметике бесконечностей посвящен ряд его недавних работ, в том числе статья "Blinking fractals and their quantitative analysis" (Chaos, Solitons & Fractals, 33(1), 50—75, 2007), использованная в этом материале. См. также www.info.deis.unical.it/~yaro/arithmetic.html, www.grossone.com.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Настройка локальной сети «компьютер-компьютер»
Настройка локальной сети «компьютер-компьютер» Ну, а теперь будем считать, что все «железо» уже подключено и настроено и вернемся к Windows: ведь просто создать сеть на «железном» недостаточно, ее нужно еще настроить! Собственно говоря, именно сетевые возможности составляют
Наука: Эллиптическая криптография
Наука: Эллиптическая криптография Автор: Сергей Николенко But the security of cryptosystems based on elliptic curves is not well understood, due in large part to the abstruse nature of elliptic curves. Few cryptographers understand elliptic curves, so there is not the same widespread understanding and consensus concerning the security of elliptic curves that RSA enjoys. Over time, this may change, but for now trying to get an evaluation of the
Наука: Математический шлягер в 3D
Наука: Математический шлягер в 3D Автор: Леонид Левкович-МаслюкПогружается ли Россия в бездну невежества?..Сегодня мы расскажем об очень интересном просветительском проекте, порожденном такими опасениями. Лозунг проекта — создание у молодежи моды на образованность и
Наука: Информация или дух?
Наука: Информация или дух? Автор: Анатолий ШалытоОдин очень сильный студент на вопрос, почему он не ходил на мои лекции, ответил, что на одной лекции был, но полученной информации ему было недостаточно.Я понял, о чем идет речь, но с ним не согласился, так как на лекциях ставлю
Наука и жизнь
Наука и жизнь Тибетский горючий лёд обогреет Китай Михаил Карпов После такого заголовка сразу же представляются огромные грузовики, гружёные льдом и снующие повсюду предприимчивые китайцы. На самом деле, всё прозаичнее: китайские власти планируют начать разработку
Наука и жизнь
Наука и жизнь "Великое объединение" для нейтронных звезд Сергей Попов (ГАИШ МГУ) Опубликовано 12 мая 2010 года В современной физике высоких энергий есть такое важное и красивое понятие, как «Великое объединение». Это та самая «теория всего» или
Наука и жизнь
Наука и жизнь Злоключения марсоходов Михаил Карпов Марсоход Opportunity празднует своего рода юбилей: длина пройденного им пути достигла 20 км. Он проехал по пескам Марса дальше, чем любое другое колёсное средство передвижения, добравшееся до этой планеты.На первый взгляд,
Наука и жизнь
Наука и жизнь Лунный краудсорсинг: исследование планет по интернету Михаил Карпов Опубликовано 26 мая 2010 года Оксфордский астрофизик Крис Линтот создал интернет-проект Moon Zoo, каждый участник которого сможет помочь учёным исследовать Луну. Проект