4.6. Методы криптографии
4.6. Методы криптографии
Проблемой защиты информации путем ее преобразования занимается криптология (kryрtos — тайный, logos – наука). Криптология разделяется на два направления – криптографию и криптоанализ. Цели этих направлений прямо противоположны.
Криптография занимается поиском и исследованием математических методов преобразования информации.
Криптоанализ занимается исследованием возможностей расшифровывания информации без знания ключей.
Современная криптография включает в себя четыре крупных раздела:
1. Симметричные криптосистемы.
2. Криптосистемы с открытым ключом.
3. Системы электронной подписи.
4. Управление ключами.
Основные направления использования криптографических методов – передача конфиденциальной информации по каналам связи, установление подлинности передаваемых сообщений, хранение информации (документов, баз данных) на носителях в зашифрованном виде.
Криптография дает возможность преобразовать информацию таким образом, что ее прочтение (восстановление) возможно только при знании ключа.
В качестве информации, подлежащей шифрованию и дешифрованию, будут рассматриваться тексты, построенные на некотором алфавите.
Под этими терминами понимается следующее. Алфавит – конечное множество используемых для кодирования информации знаков.
Текст – упорядоченный набор из элементов алфавита. Шифрование – преобразовательный процесс: исходный текст, который носит также название открытого текста, заменяется шифрованным текстом.
Дешифрование – обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный текст.
Ключ — информация, необходимая для беспрепятственного шифрования и дешифрования текстов.
Криптографическая система представляет собой семейство T [T1, T2…, Tk] преобразований открытого текста. Члены этого семейства индексируются, или обозначаются символом k; параметр k является ключом. Пространство ключей K – это набор возможных значений ключа. Обычно ключ представляет собой последовательный ряд букв алфавита.
Криптосистемы разделяются на симметричные криптосистемы и криптосистемы с открытым ключом.
В симметричных криптосистемах и для шифрования, и для дешифрования используется один и тот же ключ.
В системах с открытым ключом используются два ключа – открытый и закрытый, которые математически связаны друг с другом.
Информация шифруется с помощью открытого ключа, который доступен всем желающим, а расшифровывается с помощью закрытого ключа, известного только получателю сообщения.
Термины распределение ключей и управление ключами относятся к процессам системы обработки информации, содержанием которых является составление и распределение ключей между пользователями.
Электронной (цифровой) подписью называется присоединяемое к тексту его криптографическое преобразование, которое позволяет при получении текста другим пользователем проверить авторство и подлинность сообщения.
Криптостойкостью называется характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа (т. е. криптоанализу). Имеется несколько показателей криптостойкости, среди которых:
1) количество всех возможных ключей;
2) среднее время, необходимое для криптоанализа. Преобразование Tk определяется соответствующим алгоритмом и значением параметра k. Эффективность шифрования с целью защиты информации зависит от сохранения тайны ключа и криптостойкости шифра.
Процесс криптографического закрытия данных может осуществляться как программно, так и аппаратно. Аппаратная реализация отличается существенно большей стоимостью, однако ей присущи и преимущества: высокая производительность, простота, защищенность и т. д. Программная реализация более практична, допускает гибкость в использовании.
Для современных криптографических систем защиты информации сформулированы следующие общепринятые требования:
1) зашифрованное сообщение должно поддаваться чтению только при наличии ключа;
2) число операций, необходимых для определения использованного ключа шифрования по фрагменту шифрованного сообщения и соответствующего ему открытого текста, должно быть не меньше общего числа возможных ключей;
3) число операций, необходимых для расшифровывания информации путем перебора всевозможных ключей, должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютеров (с учетом возможности использования сетевых вычислений);
4) знание алгоритма шифрования не должно влиять на надежность защиты;
5) незначительное изменение ключа должно приводить к существенному изменению вида зашифрованного сообщения даже при использовании одного и того же ключа;
6) структурные элементы алгоритма шифрования должны быть неизменными;
7) дополнительные биты, вводимые в сообщение в процессе шифрования, должен быть полностью и надежно скрыты в шифрованном тексте;
8) длина шифрованного текста должна быть равной длине исходного текста;
9) не должно быть простых и легко устанавливаемых зависимостей между ключами, последовательно используемыми в процессе шифрования;
10) любой ключ из множества возможных ключей должен обеспечивать надежную защиту информации;
11) алгоритм должен допускать как программную, так и аппаратную реализацию, при этом изменение длины ключа не должно вести к качественному ухудшению алгоритма шифрования.
Современные алгоритмы симметричного шифрования используют как подстановку, так и перестановку. Стандартом де-факто являются несколько раундов шифрования с разными ключами, которые генерируются на основе одного общего ключа. Большинство алгоритмов имеют структуру, аналогичную структуре шифра Файстеля, разработанного в 1973 г.
Надежный алгоритм шифрования должен удовлетворять двум свойствам: диффузии и конффузии.
Диффузия – каждый бит открытого текста должен влиять на каждый бит зашифрованного текста. Суть диффузии заключается в рассеянии статистических характеристик открытого текста внутри шифрованного текста.
Конфузия – отсутствие статистической взаимосвязи между ключом и зашифрованным текстом. Даже если противник определит какие-то статистические особенности зашифрованного текста, их будет недостаточно, чтобы получить информацию о ключе.
Структура шифра Файстеля
Данный шифр относится к категории блочных. Блочные шифры предназначены для шифрования небольших блоков определенной длины. Перед зашифровыванием произвольного текста его разбивают на блоки. Затем каждый блок зашифровывается отдельно. Шифр Файстеля работает с двоичным алфавитом, т. е. открытый и зашифрованный текст представлены последовательностью битов и предназначен для реализации на ЭВМ.
На вход алгоритма шифрования подается блок открытого текста, имеющий четную длину 2l и ключ K. Блок разделяется на две равные части – правую R0 и левую L0. Далее эти части проходят m раундов обработки, после чего снова объединяются в зашифрованный текст.
Каждый i-й раунд состоит в генерации подключа Ki (на основе общего ключа K) и применении к блоку Ri некоторого зависящего от ключа преобразования F. Результат складывается с блоком Li с помощью операции XOR (исключающее или) и получается блок Ri+1. Блок Ri без изменений берется в качестве блока Li+1.
Процесс дешифрования: на вход подается зашифрованный текст, а ключи Ki вычисляются в обратном порядке.
Различные алгоритмы, использующие структуру шифра Файстеля, могут отличаться следующими параметрами:
1. Длина ключа. Чем длиннее ключ, предусмотренный алгоритмом, тем сложнее осуществить перебор. Сейчас надежной считается длина ключа не менее 1024 бит.
2. Размер блока. Чем выше размер блока, тем больше надежность шифра, но скорость операций шифрования/дешифрования снижается.
3. Число раундов обработки. С каждым новым раундом обработки надежность шифра повышается.
4. Функция раунда F – чем она сложнее, тем труднее криптоанализ шифра.
5. Алгоритм вычисления промежуточных ключей Ki.
Алгоритм DES
Ранее самым популярным алгоритмом симметричного шифрования являлся DES (Data Encrypting Standart), принятый в 1977 г. Этот алгоритм базируется на структуре шифра Файстеля с размером блока 64 бита и 56-битным ключом. Функция раунда F использует набор из восьми так называемых S-матриц. Каждая матрица состоит из 4 строк, причем каждая строка представляет собой перестановку чисел от 0 до 15 (16 столбцов). Матрицы жестко заданы. Каждая матрица получает на вход шесть бит и выдает четырехбитовый результат. Первый и последний бит входного значения задают строку матрицы, а четыре остальных – столбец. Двоичное представление числа, находящегося на их пересечении, и будет результатом преобразования. Преобразование F заключается в следующем:
1. 32-битовый блок Ri расширяется до 48 битов с помощью специальной таблицы путем дублирования некоторых 16 битов.
2. Полученный результат складывается с 48-битным подключом Ki операцией XOR.
3. Результат сложения разбивается на восемь шестибитовых блоков и каждый из них преобразуется с помощью соответствующей S-матрицы.
4. Получившийся в итоге 32-битный блок подвергается жестко заданной в алгоритме перестановке.
Долгое время DES являлся федеральным стандартом шифрования США. Этот алгоритм показывает хороший лавинный эффект, т. е. изменение одного бита открытого текста или ключа приводит к изменению многих битов зашифрованного текста. DES успешно противостоял многолетним попыткам взлома. Однако длина ключа в 56 битов при возросшей производительности ЭВМ сделала шифр потенциально уязвимым к перебору ключей, поэтому в 1997 г. был объявлен конкурс на новый алгоритм.
Алгоритм AES
Победитель конкурса был определен в 2000 г. – им стал бельгийский шифр RIJNDAEL, который был переименован в AES (Advanced
Encryption Standard). Он является нетрадиционным блочным шифром, поскольку не использует сеть Фейштеля. Каждый блок входных данных представляется в виде двумерного массива байт: 4 ? 4, 4 ? 6 или 4 ? 8 в зависимости от размера блока, который может варьироваться. В зависимости от размера блока и длины ключа алгоритм содержит от 10 до 14 раундов, в каждом из которых проводится ряд преобразований – либо над независимыми столбцами, либо над независимыми строками, либо над отдельными байтами в таблице.
Среди других современных алгоритмов симметричного шифрования шифры IDEA, Blowfish, RC5, CAST-128.
Российский стандарт цифровой подписи
Отечественный стандарт цифровой подписи (ГОСТ Р 34.10–94) вступил в силу в 1995 г. Алгоритм цифровой подписи, определяемый этим стандартом, концептуально близок американскому алгоритму DSA (Digital Signature Algorithm), который был предложен в 1991 г. Национальным институтом стандартов и технологий США для использования в стандарте цифровой подписи DSS (Digital Signature Standard). Алгоритм DSA является развитием алгоритмов цифровой подписи Эль Гамаля и К. Шнорра.
В российском стандарте цифровой подписи используются следующие параметры: p – большое простое число длиной от 509 до 512 бит либо от 1020 до 1024 бит; q – простой сомножитель числа (p ? 1), имеющий длину 254…256 бит; ? – любое целое число, меньшее (p ? 1), причем такое, что ?qmod p = 1; ? – некоторое целое число, меньшее q;
? =?? mod p.
Кроме того, этот алгоритм использует однонаправленную хэш-функцию H(·). Соответствующий российский стандарт ГОСТ Р 34.11–94 определяет хэш-функцию, основанную на использовании стандартного симметричного алгоритма ГОСТ 28147-89.
Первые три параметра p, q, ? являются открытыми и могут быть общими для всех пользователей компьютерной сети. Число ? является секретным ключом, а число ? – открытым ключом.
Чтобы подписать некоторое сообщение М, а затем проверить подпись, выполняются следующие шаги.
1. Абонент А генерирует случайное число r, причем r < q.
2. Абонент А вычисляет значения:
k = (?r mod p) mod q;
s = (?k + r (H (M))) mod q.
Если (H (M)) mod q = 0, то значение (H (M)) mod q принимают равным единице. Если k = 0, то выбирают другое значение r, и алгоритм начинают снова.
Цифровая подпись представляет собой два числа:
r mod 2256 и s mod 2256.
3. Абонент А отправляет эти числа, а также открытый текст M абоненту Б.
4. Абонент Б проверяет полученную подпись, вычисляя:
v = (H (M)) q ? 2 mod q;
z1 = (s ? v) mod q;
z2 = ((q ? k) v) mod q;
u =((?z1 ? ?z2) mod p) mod q.
Если u = r, то подпись считается подлинной. Различие между этим алгоритмом и алгоритмом DSA заключается в том, что в DSA
s = (r ? 1(? ? k + (H (M)))) mod q,
что приводит к другому уравнению проверки подлинности цифровой подписи.
В американском стандарте цифровой подписи параметр q имеет длину 160 бит, в отечественном – 256 бит, что обеспечивает более безопасную подпись.
В 2001 г. в России принят еще один стандарт цифровой подписи – ГОСТ Р 34.10-2001, который базируется на математическом аппарате эллиптических кривых, использует хэш-функцию длиной 256 бит и обладает более высокой криптостойкостью, чем предыдущий стандартный алгоритм цифровой подписи ГОСТ Р 34.11–94.
В США с 2001 г. начал действовать новый стандарт на симметричные блочные криптосистемы – AES (Advanced Encryption Standard), заменивший DES. Алгоритм допускает размеры ключей в 128, 192 и 256 бит.
Управление криптографическими ключами
Любая криптографическая система основана на использовании криптографических ключей. Под ключевой информацией понимают совокупность всех действующих в автоматизированной системе обработки информации ключей. Если не обеспечено достаточно надежное управление ключевой информацией, то, завладев ею, злоумышленник получает неограниченный доступ ко всей информации.
Управление ключами – информационный процесс, сопровождающий жизненный цикл ключей в криптосистеме и включающий реализацию следующих основных функций:
• генерация ключей;
• хранение ключей;
• распределение ключей;
• уничтожение ключей.
Безопасность любого криптографического алгоритма определяется используемым криптографическим ключом. Надежные криптографические ключи должны иметь достаточную длину и случайные значения битов.
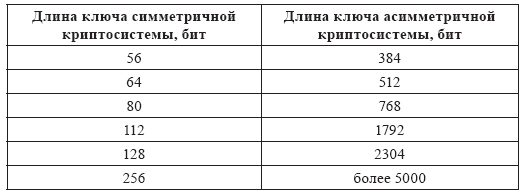
В таблице 7 приведены длины ключей симметричной и асимметричной криптосистем, которые обеспечивают одинаковую стойкость к атаке полного перебора.
Для получения ключей используются аппаратные и программные средства генерации случайных значений ключей. Как правило, применяют датчики псевдослучайных чисел. Идеальными генераторами являются устройства на основе «натуральных» (физических) случайных процессов, например на основе белого радиошума.
Таблица 7
Длины ключей для симметричных и асимметричных криптосистем при одинаковой их криптостойкости
В автоматизированных системах обработки информации со средними требованиями защищенности приемлемы программные генераторы ключей, которые вычисляют последовательность псевдослучайных чисел как сложную функцию от текущего времени и (или) числа, введенного пользователем.
В российском стандарте ГОСТ 28147-89 предусмотрена возможность генерации псевдослучайных чисел весьма высокого качества с периодом N = 232(232 ? 1).
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Службы криптографии (Cryptographic Services)
Службы криптографии (Cryptographic Services) Предоставляет три службы управления: службу баз данных каталога, которая проверяет цифровые подписи файлов Windows; службу защищенного корня, которая добавляет и удаляет сертификаты доверенного корня центра сертификации с этого
1.1.7. Методы
1.1.7. Методы Компонент TUUCode имеет три метода; один public конструктор, один protected метод и один public метод:Конструктор Create используется для создания компонента и инициализации свойств ао умолчанию (default) для Active, FileMode, Headers и About.Метод Activate используется для вызова метода UUCode во
1. Методы
1. Методы Описание метода внутри объектного типа соответствует опережающему описанию метода (forward). Таким образом, где-нибудь после описания объектного типа, но внутри той же самой области действия, что и область действия описания объектного типа, метод должен
12.1. Основы криптографии
12.1. Основы криптографии Американский математик Клод Шеннон написал работу «Теория связи в секретных системах», в которой он обобщил накопленный до него опыт разработки шифров. В этой работе указано на то, что даже в самых сложных шифрах в качестве типичных компонентов
История криптографии
История криптографии The Code Book: The Evolution of Secrecy from Mary, Queen of Scots, to Quantum Cryptography, Simon Singh, Doubleday & Company, Inc., 1999, ISBN 0-385-49531-5.The Codebreakers: The Story of Secret Writing, David Kahn, Simon & Schuster Trade, 1996, ISBN 0-684-83130-9 (обновление издания 1967 года). Эта книга описывает историю шифров и людей, взламывающих эти шифры, со
Технические аспекты криптографии
Технические аспекты криптографии Веб-сайтыhttp://www.iacr.org — Международная Ассоциация Криптологических Исследований (IACR). IACR проводит конференции по проблемам криптографии и издаёт журналы.http://www.pgpi.org — международный неофициальный веб-сайт PGP, не поддерживаемый PGP Corporation.
Политика криптографии
Политика криптографии http://www.epic.org — Electronic Privacy Information Center.http://www.crypto.org — Internet Privacy Coalition.http://www.eff.org — Electronic Frontier Foundation.http://www.privacy.org — The Privacy Page. Великолепный информационный ресурс по вопросам прав человека.http://www.cdt.org — Center for Democracy and Technology.http://www.philzimmermann.com — домашняя
Глава 1. Основы криптографии
Глава 1. Основы криптографии Юлий Цезарь не доверял гонцам. Поэтому, отправляя письма своим генералам, он заменял каждую букву A в своём сообщении на D, каждую B на E, и т. д. Только тот, кто знал правило «сдвига на 3» мог расшифровать его послание. Итак, приступим. Зашифрование
Методы
Методы Методы представляют собой процедуры и функции, объявленные внутри класса или записи. Особыми разновидностями методов являются конструкторы, деструкторы и перегруженные операции.Определение методов можно давать как внутри класса (стиль Java, C#, C++), так и вне класса
Методы Any, All
Методы Any, All Описание методовМетоды приведены для последовательности sequence of T. function Any(): boolean; Проверяет, содержит ли последовательность какие-либо элементы. function Any(predicate: T->boolean): boolean; Проверяет, удовлетворяет ли какой-либо элемент последовательности заданному
Секреты криптографии
Секреты криптографии Автор: Киви БердНеобычно тихо в истории криптографии удалось решить один весьма любопытный вопрос. Речь идет об известном сюжете из первой половины 1970-х годов, когда базовые принципы и конкретные алгоритмы криптографии с открытым ключом были
Кивино гнездо: Конфликт криптографии и бюрократии Берд Киви
Кивино гнездо: Конфликт криптографии и бюрократии Берд Киви Опубликовано 09 июля 2010 года Новая структура в составе вооруженных сил США, получившая название «киберкомандование» и базирующаяся в штаб-квартире Агентства национальной безопасности в
Глава 2 Основы криптографии
Глава 2 Основы криптографии ? Алгоритмы и стандарты шифрования? Электронная цифровая подпись? Современные технологии аутентификации. Смарт-картыКриптография– наука о математических методах обеспечения конфиденциальности (невозможности прочтения информации
Вперед.Будущее криптографии Дороти Деннинг [35]
Вперед.Будущее криптографии Дороти Деннинг[35] Для обозначения неминуемого наступления Славного Нового Мира, когда правительства в том виде, в каком они сейчас существуют, рассыплются, исчезнут и будут заменены виртуальными сообществами, свободными беспрепятственно
Послесловие к «Будущему криптографии» Дороти Деннинг [51]
Послесловие к «Будущему криптографии» Дороти Деннинг[51] С момента, когда я корректировала вышеприведенную статью (см. § 9 [антологии]) в январе 1996 года, ситуация в области криптографии сильно изменилась. Администрация Клинтона ослабила ограничения на экспорт в том же году,
Концепции криптографии
Концепции криптографии Что означает слово крипто ? Оно происходит от греческого слова «криптос» – скрытый. Поэтому целью криптографии является скрытие сути информации от посторонних лиц таким образом, чтобы с ней мог ознакомиться только тот, кому она предназначена. В