2. Правила вывода Армстронга
2. Правила вывода Армстронга
Если какое-либо базовое отношение удовлетворяет векторно определенным функциональным зависимостям, то с помощью различных специальных правил вывода можно получить другие функциональные зависимости, которым данное базовое отношение будет заведомо удовлетворять.
Хорошим примером таких специальных правил являются правила вывода Армстронга.
Но прежде чем приступать к анализу самих правил вывода Армстронга, введем в рассмотрение новый металингвистический символ «?», который называется символом метаутверждения о выводимости. Этот символ при формулировании правил записывается между двумя синтаксическими выражениями и свидетельствует о том, что из формулы, стоящей слева от него, выводится формула, стоящая справа от него.
Сформулируем теперь сами правила вывода Армстронга в виде следующей теоремы.
Теорема. Справедливы следующие правила, называемые правилами вывода Армстронга.
Правило вывода 1. ? X ? X;
Правило вывода 2. X ? Y? X ? Z ? Y;
Правило вывода 3. X ? Y, Y ? W ? Z ? X ? W ? Z;
Здесь X, Y, Z, W – произвольные подсхемы схемы отношения S. Символ метаутверждения о выводимости разделяет списки посылок и списки утверждений (заключений).
1. Первое правило вывода называется «рефлексивность» и читается следующим образом: «выводится правило: “X функционально влечет за собой X”». Это самое простое из правил вывода Армстронга. Оно выводится буквально из воздуха.
Интересно заметить, что функциональная зависимость, обладающая и левой, и правой частями, называется рефлексивной. Согласно правилу рефлексивности ограничение рефлексивной зависимости выполняется автоматически.
2. Второе правило вывода называется «пополнение» и читается таким образом: «если X функционально определяет Y, то выводится правило: “объединение подсхем X и Z функционально влечет за собой Y”». Правило пополнения позволяет расширять левую часть ограничения функциональных зависимостей.
3. Третье правило вывода называется «псевдотранзитивность» и читается следующим образом: “если подсхема X функционально влечет за собой подсхему Y и объединение подсхем Y и W функционально влекут за собой Z, то выводится правило: «объединение подсхем X и W функционально определяют подсхему Z»”.
Правило псевдотранзитивности обобщает правило транзитивности, соответствующее частному случаю W: = 0. Приведем формулярную запись этого правила:
X ?Y, Y ? Z ?X ? Z.
Необходимо отметить, что посылки и заключения, приведенные ранее, были представлены в сокращенной форме обозначениями схем функциональной зависимости. В расширенной форме им соответствуют следующие ограничения функциональных зависимостей.
Правило вывода 1. inv <X ? X> r(S);
Правило вывода 2. inv <X ? Y> r(S) ? inv <X ? Z ? Y> r(S);
Правило вывода 3. inv <X ? Y> r(S) & inv <Y ? W ? Z> r(S) ? inv<X ? W ? Z> r(S);
Проведем доказательства этих правил вывода.
1. Доказательство правила рефлексивности следует непосредственно из определения ограничения функциональной зависимости при подстановке вместо подсхемы Y – подсхемы X.
Действительно, возьмем ограничение функциональной зависимости:
Inv <X ? Y> r(S) и подставим в него X вместо Y, получим:
Inv <X ? X> r(S), а это и есть правило рефлексивности.
Правило рефлексивности доказано.
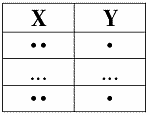
2. Доказательство правила пополнения проиллюстрируем на диаграммах функциональной зависимости.
Первая диаграмма – это диаграмма посылки:
посылка: X ? Y
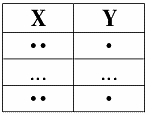
Вторая диаграмма:
заключение: X ? Z ? Y
Пусть кортежи равны на X ? Z. Тогда они равны на X. Согласно посылке они будут равны и на Y.
Правило пополнения доказано.
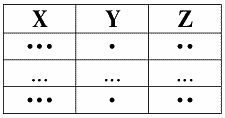
3. Доказательство правила псевдотранзитивности также проиллюстрируем на диаграммах, которых в этом конкретном случае будет три.
Первая диаграмма – первая посылка:
посылка 1: X ? Y
посылка 2: Y ? W ? Z
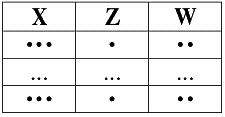
И, наконец, третья диаграмма – диаграмма заключения:
заключение: X ? W ? Z
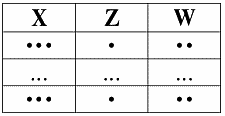
Пусть кортежи равны на X ? W. Тогда они равны и на X, и на W. Согласно Посылке 1, они будут равны и на Y. Отсюда, согласно Посылке 2, они будут равны и на Z.
Правило псевдотранзитивности доказано.
Все правила доказаны.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Правила@
Правила@ Правила @ начинаются с ключевого слова @, непосредственно за которым следует идентификатор (например, @import, @page). Каждый из этих идентификаторов далее рассмотрим подробнее.Все же надо отметить, что браузер с поддержкой CSS будет игнорировать все правила @import, которые
4.2.3. Суффиксные правила
4.2.3. Суффиксные правила Суффиксные правила — это другая область, в которой вам нужно решить, писать ли стандартные make-файлы или использовать расширения GNU. Стандартные суффиксные правила намного ограниченнее, нежели шаблонные правила GNU, но во многих ситуациях
Правила
Правила Правила используются в таблицах стилей для особых нужд.charsetЗадает текстовую кодировку для внешней таблицы стилей.@charset {Кодировка};Пример:@charset "windows-1251";Может использоваться только во внешних таблицах стилей; должна быть первой строкой в файле. Поддерживается IE
§ 165. Три правила про вы
§ 165. Три правила про вы 7 сентября 2010В русском языке существует местоимение вы, к которому прилагаются довольно простые правила употребления и неупотребления.Вы всегда пишется с маленькойСовершенно невыносима рекламно-подобострастная манера писать Вы с заглавной
1.5. Правила
1.5. Правила Предположим, мы хотим сформулировать утверждение, что Джону нравятся все люди. Один из способов сделать это заключается в записи для каждого человека, упоминаемого в базе данных, отдельного факта:нравится(джон,альфред). нравится(джон,бертран).
2.1. Синтаксические правила
2.1. Синтаксические правила Синтаксические правила языка описывают допустимые способы соединения слов. В соответствии с нормами английского языка предложение «I see a zebra» («я вижу зебру») является синтаксически правильным в отличие от предложения «zebra see I а» («зебра видит
Правила для отступов
Правила для отступов В каких же строках программного кода следует сделать отступ и какой по величине? Нужно установить отступы одного размера для связанных по смыслу операторов, чтобы связь между такими операторами была зрительно очевидной. Конкретнее говоря,
15.4.3. Правила make
15.4.3. Правила make Некоторые из наиболее интенсивно используемых правил в типичных make-файлах вообще не выражают зависимостей. Они позволяют связать небольшие процедуры, которые разработчик хочет механизировать, например, создание дистрибутивного пакета или удаление всех
15.4.3. Правила make
15.4.3. Правила make Некоторые из наиболее интенсивно используемых правил в типичных make-файлах вообще не выражают зависимостей. Они позволяют связать небольшие процедуры, которые разработчик хочет механизировать, например, создание дистрибутивного пакета или удаление всех
3. Производные правила вывода
3. Производные правила вывода Другим примером правил, с помощью которых можно, при необходимости вывести новые правила функциональной зависимости, являются так называемые производные правила вывода.Что это за правила, как они получаются?Известно, что если из одних
4. Полнота системы правил Армстронга
4. Полнота системы правил Армстронга Пусть F(S) — заданное множество функциональных зависимостей, заданных над схемой отношения S.Обозначим через inv <F(S)> ограничение, накладываемое этим множеством функциональных зависимостей. Распишем его: Inv <F(S)> r(S) = ?X ? Y ?F(S) [inv <X ?
5.1.1. Общие правила
5.1.1. Общие правила Ваш компьютер будет «жить долго и счастливо», если вы станете придерживаться следующих правил эксплуатации:Бережно обращайтесь с компьютером и периферийными устройствами. Компьютер не простит вам, если вы уроните его со стола. При транспортировке
Правила об именах
Правила об именах (В этом разделе мы только формализуем сказанное выше, поэтому при первом чтении книги его можно пропустить.)Мы уже видели, что в случае возможной неоднозначности конфликты имен пресекаются, хотя некоторые ситуации бывают вполне корректны. Чтобы в
Правила типизации
Правила типизации Наша ОО-нотация является статически типизированной. Ее правила типов были введены в предыдущих лекциях и сводятся к трем простым требованиям.[x]. При объявлении каждой сущности или функции должен задаваться ее тип, например, acc: ACCOUNT. Каждая подпрограмма