5. Производные операции

5. Производные операции

Итак, мы рассмотрели различные варианты операций соединения, а именно операции внутреннего соединения, левого, правого и полного внешнего соединения, которые являются производными восьми исходных операций реляционной алгебры: унарных операций выборки, проекции, переименования и бинарных операций объединения, пересечения, разности, декартова произведения и естественного соединения. Но и среди этих исходных операций есть свои примеры производных операций.

1. Например, операция пересечения двух отношений является производной от операции разности этих же двух отношений. Покажем это.

Операцию пересечения можно выразить следующей формулой:

r1(S) ? r2(S) = r1 r1 r2

или, что дает тот же результат:

r1(S) ? r2(S) = r2 r2 r1;

2. Еще одним примером, производной базовой операции от восьми исходных операций является операция естественного соединения. В самом общем виде эта операция является производной от бинарной операции декартового произведения и унарных операций выборки, проекции и переименования атрибутов. Однако, в свою очередь, операция внутреннего соединения является производной операцией от той же операции декартового произведения отношений. Поэтому, чтобы показать, что операция естественного соединения – производная операция, рассмотрим следующий пример.

Сравним приведенные ранее примеры для операций естественного и внутреннего соединений.

Пусть нам даны два отношения r1(S1) и r2(S2) которые будут выступать в качестве операндов. Они равны:

r1(S1):

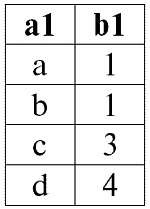
r2(S2):

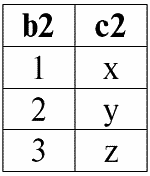
Как мы уже получали ранее, результатом операции естественного соединения этих отношений будет являться таблица следующего вида:

r3(S3) ? r1(S1) ? r2(S2):

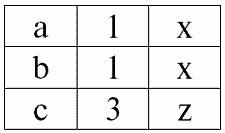
А результатом внутреннего соединения этих же отношений r1(S1) и r2(S2) по условию P = (b1 = b2) будет следующая таблица:

r4(S4) ? r1(S1) ? P r2(S2):

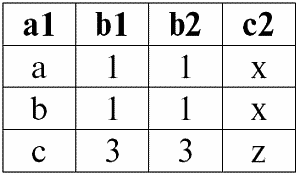
Сравним эти два результата, получившиеся новые отношения r3(S3) и r4(S4).

Ясно, что операция естественного соединения выражается через операцию внутреннего соединения, но, что главное, с условием соединения специального вида.

Запишем математическую формулу, описывающую действие операции естественного соединения как производную операции внутреннего соединения.

r1(S1) ? r2(S2) = { ? <?1> r1 ? E ?< ?2>r2}[S1 ? S2],

где E — условие соединимости кортежей;

E= ?a ?S1 ? S2 [IsNull (b1) & IsNull (2) ?b1 = b2];

b1 = ?1 (name(a)), b2 = ?2 (name(a));

Здесь одна из функций переименования ?1 является тождественной, а другая функция переименования (а именно – ?2) переименовывает атрибуты, на которых наши схемы пересекаются.

Условие соединимости E для кортежей записывается в общем виде с учетом возможных появлений Null-значений, ведь операция внутреннего соединения (как уже было сказано выше) является производной операцией от операции декартового произведения двух отношений и унарной операции выборки.

Более 800 000 книг и аудиокниг! 📚

Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением

ПОЛУЧИТЬ ПОДАРОК

Данный текст является ознакомительным фрагментом.