Лекция № 5. Реляционная алгебра. Бинарные операции

Лекция № 5. Реляционная алгебра. Бинарные операции

1. Операции объединения, пересечения, разности

У любых операций есть свои правила применимости, которые необходимо соблюдать, чтобы выражения и действия не теряли смысла. Бинарные теоретико-множественные операции объединения, пересечений и разности могут быть применены только к двум отношениям обязательно с одной и той же схемой отношения. Результатом таких бинарных операций будут являться отношения, состоящие из кортежей, удовлетворяющих условиям операций, но с такой же схемой отношения, как и у операндов.

1. Результатом операции объединения двух отношений r₁(S) и r₂(S) будет новое отношение r₃(S), состоящее из тех кортежей отношений r₁(S) и r₂(S), которые принадлежат хотя бы одному из исходных отношений и с такой же схемой отношения.

Таким образом, пересечение двух отношений – это:

r₃(S) = r₁(S) ? r₂(S) = {t(S) | t ?r₁ ?t ?r₂};

Для наглядности, приведем пример в терминах таблиц:

Пусть даны два отношения:

r₁(S):

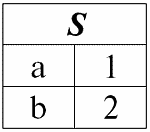
r₂(S):

Мы видим, что схемы первого и второго отношений одинаковы, только имеют различной количество кортежей. Объединением этих двух отношений будет отношение r₃(S), которому будет соответствовать следующая таблица:

r3(S) = r₁(S) ? r₂(S):

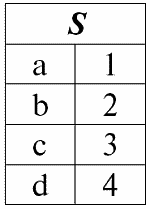
Итак, схема отношения S не изменилась, только выросло количество кортежей.

2. Перейдем к рассмотрению следующей бинарной операции – операции пересечения двух отношений. Как мы знаем еще из школьной геометрии, в результирующее отношение войдут только те кортежи исходных отношений, которые присутствуют одновременно в обоих отношениях r₁(S) и r₂(S) (снова обращаем внимание на одинаковую схему отношения).

Операция пересечения двух отношений будет выглядеть следующим образом:

r₄(S) = r₁(S) ? r₂(S) = {t(S) | t ? r₁ & t ? r₂};

И снова рассмотрим действие этой операции над отношениями, представленными в виде таблиц:

r₁(S):

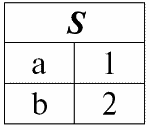
r₂(S):

Согласно определению операции пересечением отношений r₁(S) и r₂(S) будет новое отношение r₄(S), табличное представление которого будет выглядеть следующим образом:

r₄(S) = r₁(S) ? r₂(S):

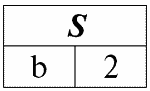
Действительно, если посмотреть на кортежи первого и второго исходного отношений, общий среди них только один: {b, 2}. Он и стал единственным кортежем нового отношения r₄(S).

3. Операция разности двух отношений определяется аналогичным с предыдущими операциями образом. Отношения-операнды, так же, как и в предыдущих операциях, должны иметь одинаковые схемы отношения, тогда в результирующее отношение войдут все те кортежи первого отношения, которых нет во втором, т. е.:

r₅(S) = r₁(S) r₂(S) = {t(S) | t ? r₁ & t ? r₂};

Уже хорошо знакомые нам отношения r₁(S) и r₂(S), в табличном представлении выглядящие следующим образом:

r₁(S):

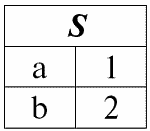
r₂(S):

Мы рассмотрим как операнды в операции пересечения двух отношений. Тогда, следуя данному определению, результирующее отношение r5(S) будет выглядеть следующим образом:

r₅(S) = r₁(S) r₂(S):

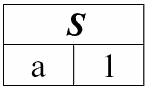
Рассмотренные бинарные операции являются базовыми, на них основываются другие операции, более сложные.

Данный текст является ознакомительным фрагментом.