4. Null-значения и логические операции

4. Null-значения и логические операции

Обычно в системах управления базами данных непосредственно поддерживаются только три логические операции: отрицание ¬, конъюнкция & и дизъюнкция ?. Операции следования ? и равносильности ? выражаются через них с помощью подстановок:

(x ? y) ? (¬x ? y);

(x ? y) ? (x ? y) & (y ? x);

Заметим, что эти подстановки полностью сохраняются и при использовании Null-значений.

Интересно, что при помощи операции отрицания «¬» любая из операций конъюнкция & или дизъюнкция ? может быть выражена одна через другую следующим образом:

(x & y) ?¬ (¬x ?¬y);

(x ? y) ? ¬ (¬x & ¬y);

На эти подстановки, как и на предыдущие, Null-значения влияния не оказывают.

А теперь приведем таблицы истинности логических операций отрицания, конъюнкции и дизъюнкции, но кроме привычных значений True и False, используем также Null-значение в качестве операндов. Для удобства введем следующие обозначения: вместо True будем писать t, вместо False – f, а вместо Null – n.

1. Отрицание ¬x.

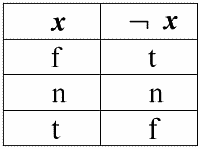
Стоит отметить следующие интересные моменты касательно операции отрицания с использованием Null-значений:

1) ¬¬x ? x – закон двойного отрицания;

2) ¬Null ? Null – Null-значение является неподвижной точкой.

2. Конъюнкция x & y.

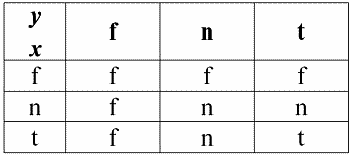
Эта операция также имеет свои свойства:

1) x & y ? y & x– коммутативность;

2) x & x ? x – идемпотентность;

3) False & y ? False, здесь False – поглощающий элемент;

4) True & y ? y, здесь True – нейтральный элемент.

3. Дизъюнкция x ? y.

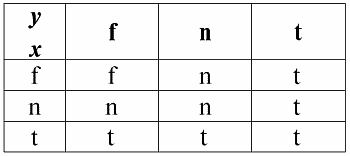
Свойства:

1) x ? y ? y ? x – коммутативность;

2) x ? x ? x – идемпотентность;

3) False ? y ? y, здесь False – нейтральный элемент;

4) True ? y ? True, здесь True – поглощающий элемент.

Исключение из общего правила составляют правила вычисления логических операций конъюнкция & и дизъюнкция ? в условиях действия законов поглощения:

(False & y) ? (x & False) ? False;

(True ? y) ? (x ? True) ? True;

Эти дополнительные правила формулируются для того, чтобы при замене Null-значения значениями False или True результат бы все равно не зависел бы от этого значения.

Как и ранее было показано для других типов операций, применение Null-значений в логических операциях могут также привести к неожиданным значениям. Например, логика на первый взгляд нарушена в законе исключения третьего (x ? ¬x) и в законе рефлексивности (x = x), поскольку при x ? Null имеем:

(x ? ¬x), (x = x) ? Null.

Законы не выполняются! Объясняется это так же, как и раньше: при подстановке Null-значения в выражение информация о том, что это значение сообщается одной и той же переменной теряется, а в силу вступает общее правило работы с Null-значениями.

Таким образом, делаем вывод: при выполнении логических операций с Null-значениями в качестве операнда эти значения определяются системами управления базами данных как применимое, но неизвестное.

Данный текст является ознакомительным фрагментом.